Файл: Расчетнографическая работа по дисциплине механика.docx

где 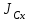- момент инерции колеса относительное его оси вращения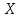 , проходящей через центр колеса. Он рассчитывается по формуле

.

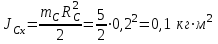(5.0)

Подставим (5.0) в (5.0) и получим:

,

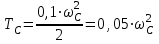(5.0)

Тело совершает плоскопараллельное движение. Его кинетическая энергия определяется как сумма кинетических энергий поступательного движения центра масс со скоростью 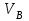и вращательного движения относительно центра масс с угловой скоростью :

,

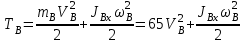(5.0)

где 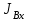- момент инерции колеса относительное его оси вращения , проходящей через центр масс, рассчитываемый по формуле: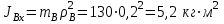

.

(5.0)

Подставим (5.0) в (5.0) и получим:

,

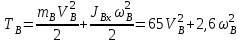(5.02)

Воспользуемся соотношениями между скоростями тел для рассматриваемой механической системы, которые были определены в разделе 2:

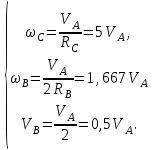(5.0)

Подставим выражения (5.0) в формулы (5.0) и Error: Reference source not found, получим:

---

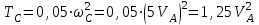,	(5.0)
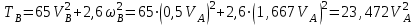.	(5.0)

Просуммировав по формуле (5.0) с учетом (5.0), (5.0) и (5.0) кинетические энергии всех тел системы, определим кинетическую энергию всей системы

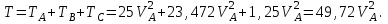(5.0)

5.4. Работа внешних сил, действующих на механическую систему

Выбрав на рис, 5.2 направление вектора скорости, мы указываем на рис. 5.3 перемещение 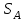для тела . Этому перемещению соответствуют перемещения , показанные на рис. 5.4.

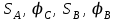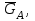
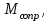
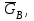
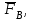
Нам необходимо определить на перемещениях работу только внешних сил, приложенных к данной системе. Все внешние силы (пары сил), действующие на данную систему и совершающие работу ( 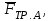и 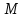) показаны на рис. 5.3, причем сила 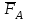(действующая на тело А, работу не совершает, т.к. перпендикулярна перемещению тела А) и 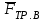(также не совершает работу, т.к. приложена в мгновенном центре скоростей колеса В).

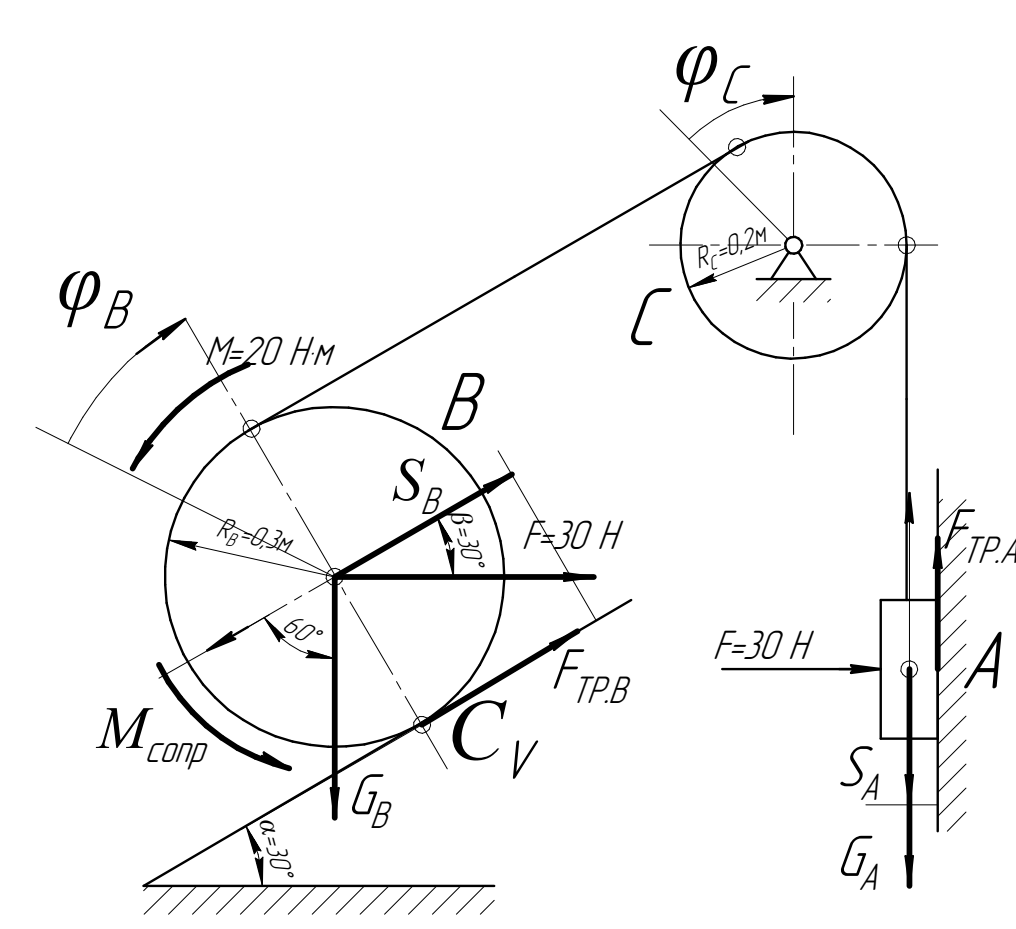Рис. 5.3. Перемещения тел механической системы и действующие на систему внешние силы

---

Зависимости углов поворота и перемещений тел от перемещения получены ранее в задаче, такие же, как и для скоростей, и они имеют вид: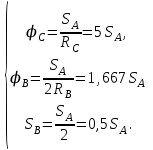

(5.07)

Все внешние силы показаны на рис. 5.3 утолщенными сплошными стрелками.

Определим совершаемые внешними силами работы.

5.4.1. Работа внешних сил, действующих на тело

Внешними силами для рассматриваемой механической системы, непосредственно приложенными к телу являются сила тяжести нормальная реакция 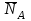, сила трения скольжения 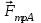, действующая на груз А со стороны вертикальной плоскости на тело , а также приложенные к телу А сила 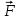(рис. 5.3).

Для определения работ этих сил, изобразим отдельно тело на вертикальной плоскости и покажем приложенные к телу перечисленные выше силы 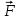, 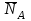и 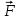(рис. 5.4). Кроме этого, применяя метод сечений, рассечем нить в точке 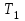и, отбрасывая верхнюю часть нити, заменим ее действие внутренней продольной силой натяжения нити 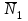, которая в итоге действует на изображенное тело через гибкую нить (рис. 5.4,

---

).

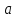Сила для рассматриваемой механической системы является внутренней и ее работа в данном случае рассчитываться не будет.

Но по отношению к телу данная сила является внешней силой и, следовательно, она определяет движение тела .

Запишем для тела основные дифференциальные уравнения динамики на оси координат в соответствии с рис. 5.4, :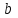

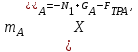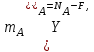(5.0)

где - масса тела , 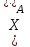- ускорение тела .

Величина силы тяжести 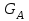определяется формулой:

,

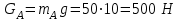(5.0)

где 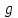- ускорение свободного падения ( ).

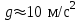Для определения величины нормальной реакции из второго уравнения (5.0) и учитывая, что на направлении нормали 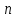к наклонной поверхности (рис. 5.4) движение отсутствует, получим

.

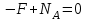(5.0)

Из (5.0) получаем:

.

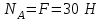(5.01)

---

Зная 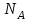, определим силу трения скольжения

.

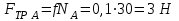(5.02)

Перемещение тела показано на рис. 5.4 вектором .

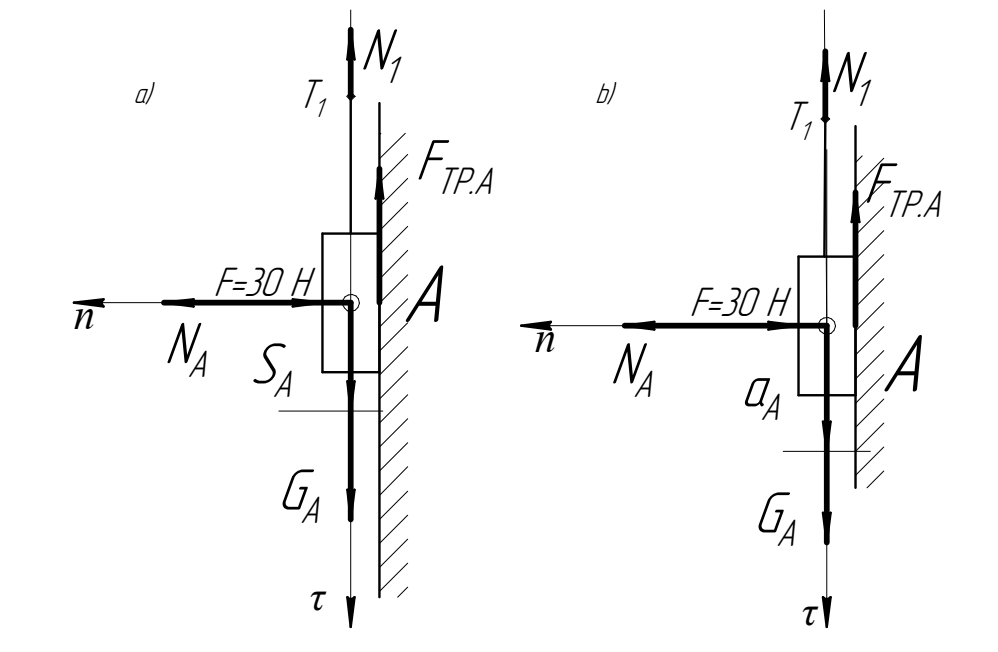Рис. 5.4. Тело и действующие на него внешние силы

Для определения работы силы на данном перемещении (рис. 5.4, ). Работа силы является положительной и в итоге определяется выражением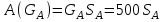

.

(5.03)

Работа силы трения скольжения 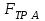является отрицательной и с учетом Error: Reference source not found определяется выражением

.

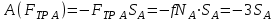(5.04)

В направлении нормальной реакции 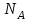и силы F, действующей на груз,тело не перемещается, и поэтому работы этих сил равны нулю: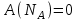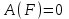

, .

(5.05)

В итоге получаем, что сумма работ всех внешних сил, приложенных к телу , определяется выражениями: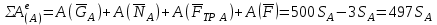

.

(5.06)

---