Добавлен: 18.10.2024
Просмотров: 28
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Определение реакций связей для двухопорной балки
Определение реакций связей для консольной балки
Определение траектории, скорости и ускорения точки по заданным уравнениям ее движения
Кинематический анализ механической системы при плоском движении
Применение теоремы об изменении кинетической энергии к изучению движения механической системы
5.4.2. Работа внешних сил, действующих на тело

Из всех внешних сил, действующих на рассматриваемую механическую систему, непосредственно на тело
 действует сила тяжести
действует сила тяжести 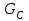 и реакции неподвижного шарнира
и реакции неподвижного шарнира 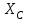 и
и 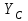 (рис. 5.5).
(рис. 5.5).Точки приложения данных сил не перемещаются, и значит, что и работы данных сил равны нулю:
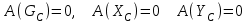 . . | (5.07) |
Действующие внешние силы на тело
 показаны на рис. 5.5.
показаны на рис. 5.5. 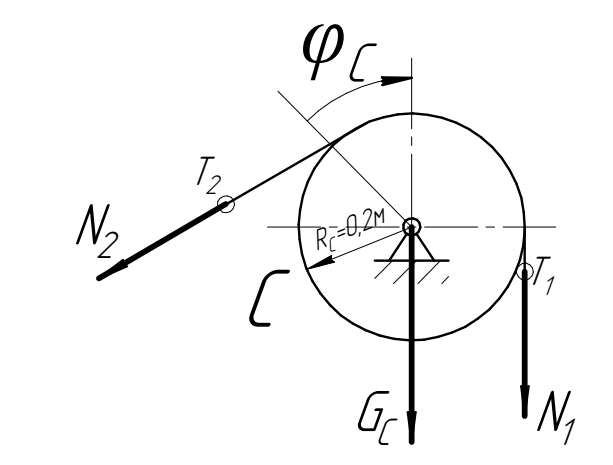 |
| Рис. 5.5. Тело  и действующие на него внешние силы и действующие на него внешние силы |
Запишем для тела
 основное уравнение динамики в соответствии с рис. 5.5:
основное уравнение динамики в соответствии с рис. 5.5: 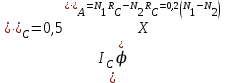 , , | (5.28) |
где
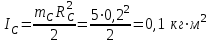 - момент инерции тела
- момент инерции тела  ,
, 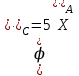 - угловое ускорение тела
- угловое ускорение тела  .
.Значение силы натяжения из (5.28)
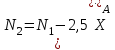 , , | (5.28а) |
5.4.3. Работа внешних сил, действующих на тело

Внешними силами для рассматриваемой механической системы, непосредственно приложенными к телу
 являются сила тяжести
являются сила тяжести  нормальная реакция
нормальная реакция 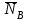 , сила трения в точке касания колеса с плоскостью
, сила трения в точке касания колеса с плоскостью 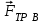 , момент
, момент 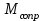 сил сопротивления качению колеса В, а так же приложенные к колесу В сила
сил сопротивления качению колеса В, а так же приложенные к колесу В сила  и момент пары сил М. (рис. 5.3).
и момент пары сил М. (рис. 5.3).Для определения работ этих сил, изобразим отдельно тело
 на наклонной плоскости и покажем приложенные к телу перечисленные выше силы
на наклонной плоскости и покажем приложенные к телу перечисленные выше силы 
 ,
, 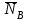 и
и 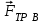 и пары сил
и пары сил 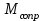 ,
,  (рис. 5.6). Кроме этого, применяя метод сечений, рассечем нить в точке
(рис. 5.6). Кроме этого, применяя метод сечений, рассечем нить в точке 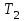 и отбрасывая верхнюю часть нити, заменим ее действие внутренней продольной силой натяжения нити
и отбрасывая верхнюю часть нити, заменим ее действие внутренней продольной силой натяжения нити 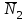 , которая в итоге действует на изображенное тело
, которая в итоге действует на изображенное тело  через гибкую нить (рис. 5.6).
через гибкую нить (рис. 5.6).Сила
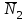 для рассматриваемой механической системы является внутренней и ее работа в данном случае рассчитываться не будет.
для рассматриваемой механической системы является внутренней и ее работа в данном случае рассчитываться не будет.Но по отношению к телу
 данная сила
данная сила
 является внешней силой и, следовательно, она определяет движение тела
является внешней силой и, следовательно, она определяет движение тела  .
.Запишем для тела
 основные дифференциальные уравнения движения в соответствии с рис. 5.6 (колесо В, движется плоскопараллельно без скольжения (что обусловлено наличием силы трения в точке касания колеса с плоскостью):
основные дифференциальные уравнения движения в соответствии с рис. 5.6 (колесо В, движется плоскопараллельно без скольжения (что обусловлено наличием силы трения в точке касания колеса с плоскостью): 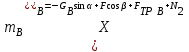 , ,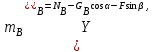 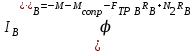 | (5.29) |
где
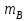 - масса тела
- масса тела  ,
, 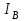 - момент инерции тела
- момент инерции тела  .
.Величина силы тяжести
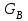 определяется формулой:
определяется формулой: 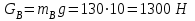 , , | (5.30) |
где
 - ускорение свободного падения (
- ускорение свободного падения ( ).
).Для определения величины нормальной реакции
 спроецируем второе дифференциальное уравнение (5.0) на направление нормали
спроецируем второе дифференциальное уравнение (5.0) на направление нормали  к наклонной поверхности (рис. 5.6), и учитывая, что в направление оси
к наклонной поверхности (рис. 5.6), и учитывая, что в направление оси  движение колеса
движение колеса  отсутствует, получим
отсутствует, получим 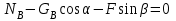 . . | (5.31) |
Из (5.0) получаем:
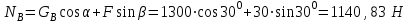 . . | (5.32) |
Зная
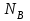 , определим момент трения качения, действующий на колесо
, определим момент трения качения, действующий на колесо 
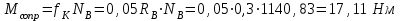 . . | (5.33) |
Из кинематики известно, что связь между ускорениями в данной механической системе можно выразить следующим образом:
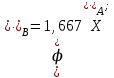
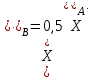
С учетом этих соотношений дифференциальные уравнения движения (5.29) принимают вид
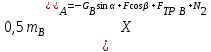 , ,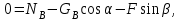 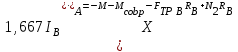 | (5.34) |
или с учетом действующей массы колеса и его момента инерции
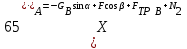 , ,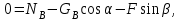 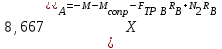 | (5.35) |
Из первого уравнения системы (5.35) можно определить значение силы трения, приложенной в точке касания колеса
 с плоскостью
с плоскостью 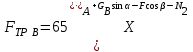 , , | (5.36) |
Перемещение тела
 показано на рис. 5.6 вектором
показано на рис. 5.6 вектором 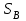 .
. 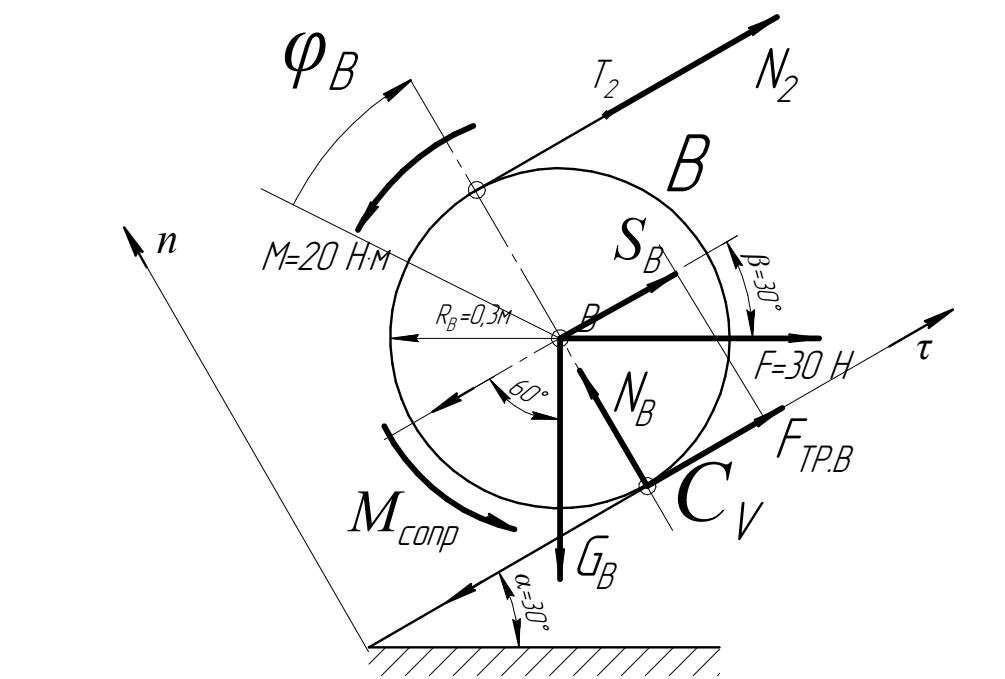 |
| Рис. 5.6. Тело  и действующие на него внешние силы и действующие на него внешние силы |
Определим работу силы

