Файл: Программа работы.doc

Пример 2. Для нахождения делителей числа необходимо взять в степени или , умножить на в степени или , на в степени или и на в степени или .

В этих условиях число всех делителей есть произведение числа способов выбора степени для каждого простого делителя, которое, в свою очередь, равно 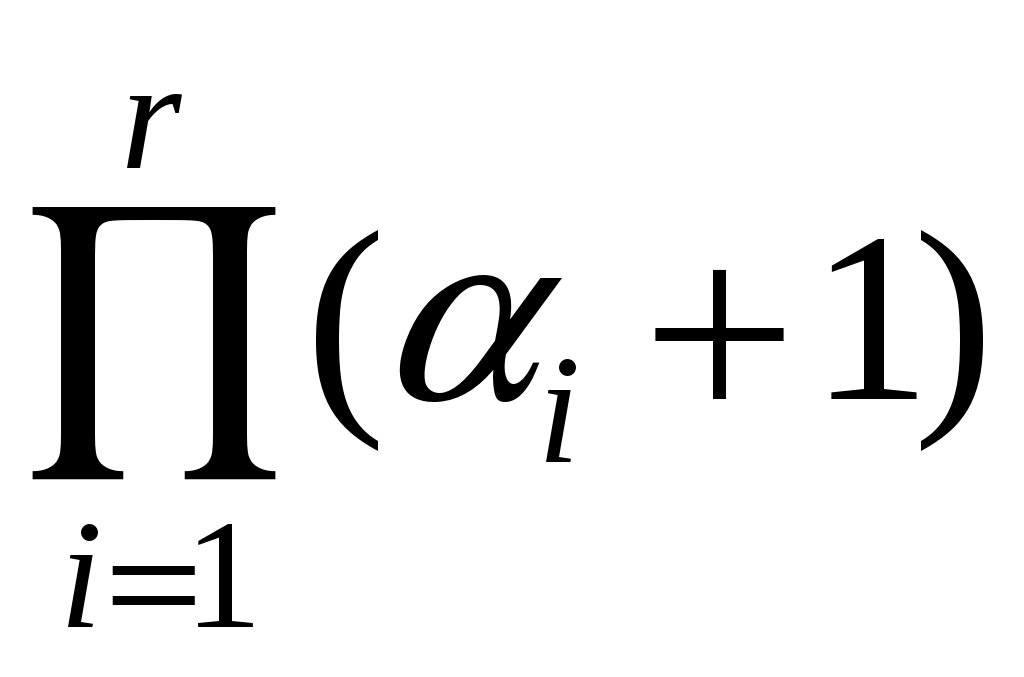. Иначе говоря, число имеет различных делителей [8,9].
Пример 3. Число имеет различных делителей.
Определение 6. Наибольшим общим делителем двух данных чисел и (обозначается ), не равных одновременно нулю, называется наибольшее целое число , делящее одновременно

---

и .
Нетрудно показать, что приведенное выше определение эквивалентно следующему.

Определение 7. − есть единственное целое положительное число, которое делит и , и делится при этом на любой их общий делитель.
Из школьного курса математики известен следующий способ нахождения наибольшего общего делителя двух положительных чисел по известному разложению на множители. Для отыскания необходимо взять все простые числа, входящие в оба разложения, и каждое возвести в степень, равную минимуму из двух соответствующих показателей.
Пример 4. Пусть дано и . Тогда .
Определение 8. Наименьшим общим кратным двух данных чисел и (обозначается ), не равных одновременно нулю, называется наименьшее целое положительное число , делящееся одновременно на и .
Имея разложение на простые множители чисел и , можно получить значение , взяв все простые числа, входящие хотя бы в одно из разложений, и каждое возвести в степень, равную максимальной из имеющихся в двух разложениях.

---

Кроме того, нетрудно показать, что наибольший общий делитель и наименьшее общее кратное связаны следующим соотношением:

.

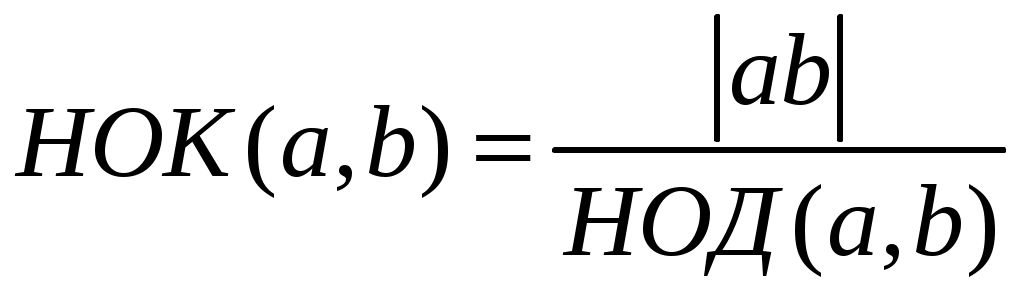1.1.2 Использование алгоритма Евклида для решения теоретико-числовых задач криптологии

Рассмотренный выше метод отыскания двух чисел основывается на использовании представления этих чисел в виде произведения простых множителей. Однако на практике такой метод мало применим, так как разложение числа, как правило, неизвестно, и его отыскание (как будет показано в дальнейшем) является сложной математической задачей.

Другим, наиболее известным способом отыскания наибольшего общего делителя двух чисел является алгоритм, впервые изложенный в трудах древнегреческого математика Евклида (IV-III вв. до н.э.

Алгоритм Евклида заключается в следующем.

Пусть , где и мы хотим найти . Разделим на с остатком , . Если , то разделим на : , и т.д. Получим последовательность равенств с убывающими остатками :

.

(2)

---

где

Если — последний ненулевой остаток, то . , в этом случае .
Пример 5. Найти .

Решение:












Таким образом .
Для практического использования приведенного алгоритма важнейшим является вопрос о времени его выполнения.
Теорема 1. При алгоритм Евклида позволяет вычислить за время порядка .
Схема доказательства. Для доказательства данной теоремы достаточно показать, что за каждые два шага алгоритма остаток уменьшается, по крайней мере, вдвое [9]. Таким образом результат работы алгоритма достигается не позднее чем через делений чисел разрядностью, не превосходящих каждое.
Теорема 2. Наибольший общий делитель двух чисел и , где , можно представить в виде линейной комбинации этих чисел

---

с целыми коэффициентами , за время порядка .
Схема доказательства. Для доказательства теоремы достаточно показать [8,9], что представление числа может быть найдено путем последовательного выражения через все более ранние остатки в алгоритме Евклида, на что будет затрачено одно умножение и одно сложение или вычитание. Поскольку количество операций реализующих сложение есть величина более низкого порядка, то получаем искомую оценку времени.
Определение 9. Два целых числа и называются взаимно простыми, если , т.е. если они не имеют общих делителей больших 1.
Определение 10. Для любого целого положительного числа функция Эйлера определяется как число неотрицательных целых , меньших и взаимно простых с :

.

Из определения следуют следующие свойства функции Эйлера:

1. .

2. Для любого простого

.

---