Файл: Программа работы.doc

.

Схема доказательства: Для доказательства теоремы необходимо представить в виде и воспользоваться теоремой 2 и свойствами сравнений [15].
Следствие: Если то обратный элемент (из условия ) может быть найден за время двоичных операций.
Замечание: Если , то под отрицательной степенью подразумевается -я степень обратного класса вычетов, т.е. класс вычетов, содержащий -ю степень любого целого числа , такого, что .

1.2.2. Использование свойств сравнений для решения теоретико-числовых задач криптологии

Подробное рассмотрение свойств сравнений позволяет получить следующий важный результат [8,9].
Теорема 4 (малая теорема Ферма). Пусть − простое число. Любое целое число удовлетворяет сравнению , и любое целое число , не делящееся на , удовлетворяет сравнению

---

.
Из условий данной теоремы несложно получить следствие.
Следствие. Если не делится на и если , то .
Пример 6. Найти последнюю цифру в записи числа в системе счисления по основанию 7.

Решение: Пусть , т.к. , то

. Следовательно, последняя цифра равна 2.
Не менее важное свойство сравнений отражает т.н. китайская теорема об остатках.
Теорема 5 (китайская теорема об остатках). Пусть требуется решить систему сравнений по различным модулям:



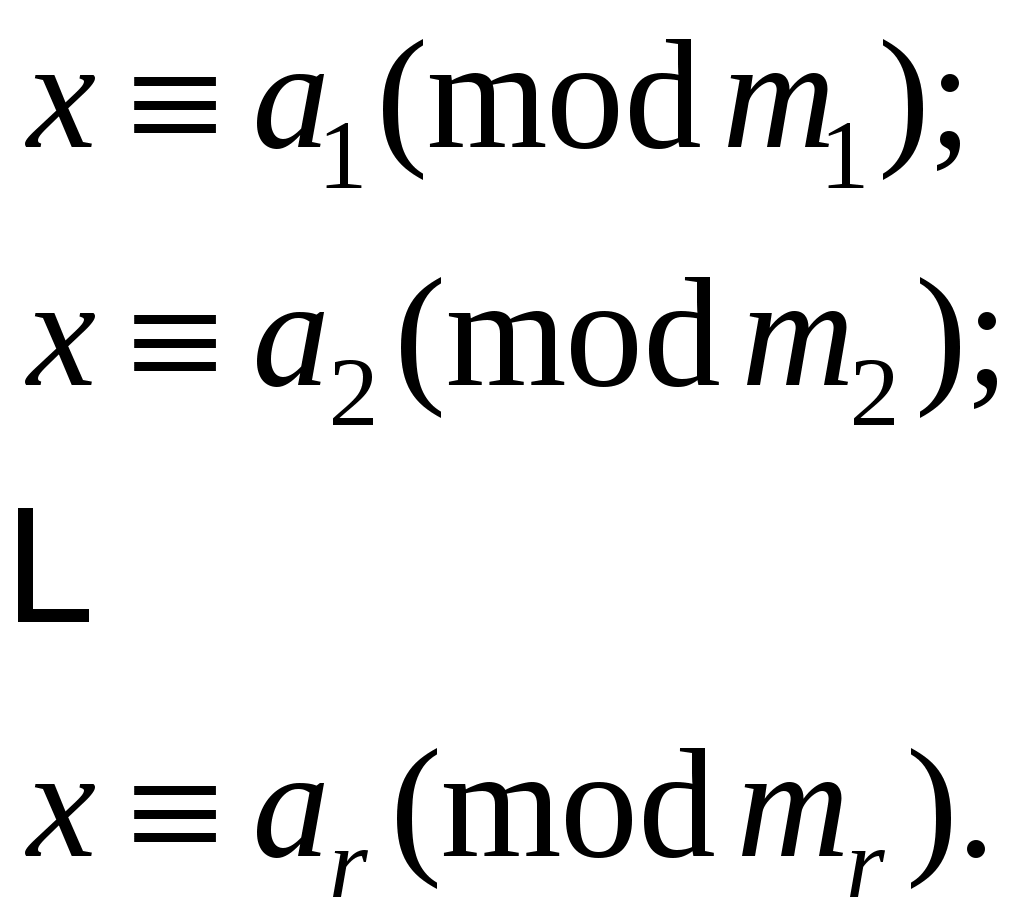
причем любые два модуля сравнения взаимно просты относительно друг друга: . Тогда эта система разрешима, и любые два решения сравнимы по модулю .

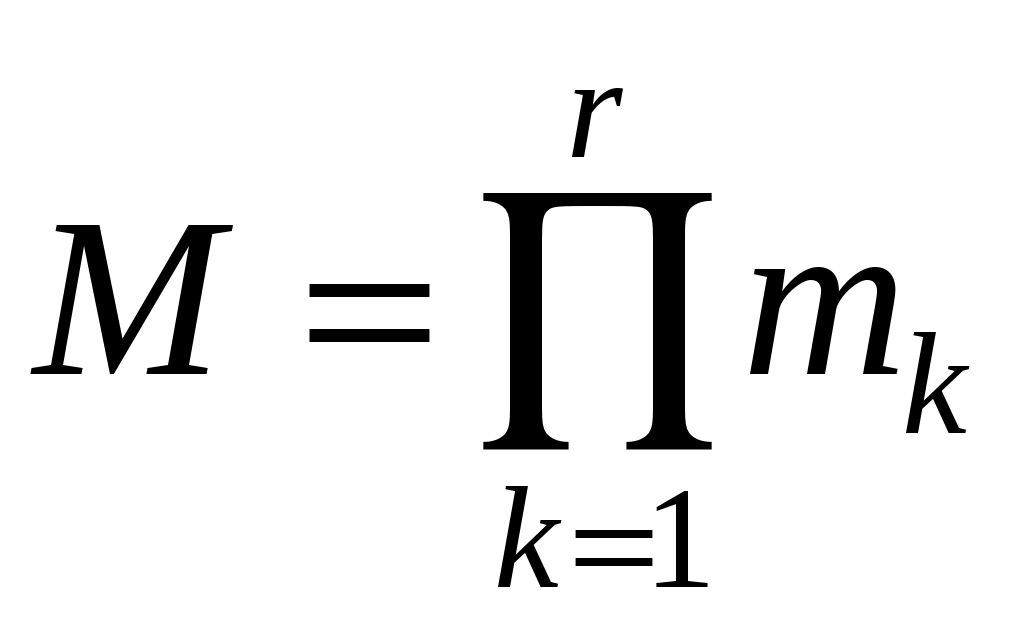Данная теорема позволяет сформулировать следующее важное следствие.
Следствие. Функция Эйлера обладает свойством «мультипликативности», т.е.

.
Теорема 6. Пусть известно, что есть произведение двух простых чисел и . Тогда зная эти числа и , можно найти за время порядка

---

и обратно, зная и , можно найти и за время порядка .
Доказательство. Утверждение очевидно, если − четно, т.к. в этом случае , и ; поэтому рассмотрим случай когда − нечетно. В силу мультипликативности функции Эйлера для получаем . Таким образом, значение может быть получено с помощью одного сложения и одного вычитания.

Обратно, предположим, что известны и , и требуется найти и . Для неизвестных величин и известны их произведение и сумма . Обозначим последнее выражение через (отметим, — число четное). Но два числа, произведение которых равно

---

, а сумма , по теореме Виета должны быть корнями квадратного уравнения . Итак и равно . Наибольшее время при вычислении занимает процедура извлечения квадратного корня: на нее требуется двоичных операций [9].
Рассмотрим обобщение малой теоремы Ферма, сделанное Эйлером.
Теорема 7 (теорема Эйлера).

.
Схема доказательства. Для начала необходимо доказать справедливость утверждения для случая, когда есть степень простого числа: . Выполняя индукцию по , при , получаем малую терему Ферма. Рассматривая биномиальные коэффициенты в выражении , получаем доказательство частного случая.

В дальнейшем, используя мультипликативность функции Эйлера и тот факт, что степени различных простых чисел взаимно просты, доказывается и общий случай [12-14].
Следствие. Если и — наименьший неотрицательный вычет по модулю , то

---

.
Пример 7. Вычислить .

Решение:


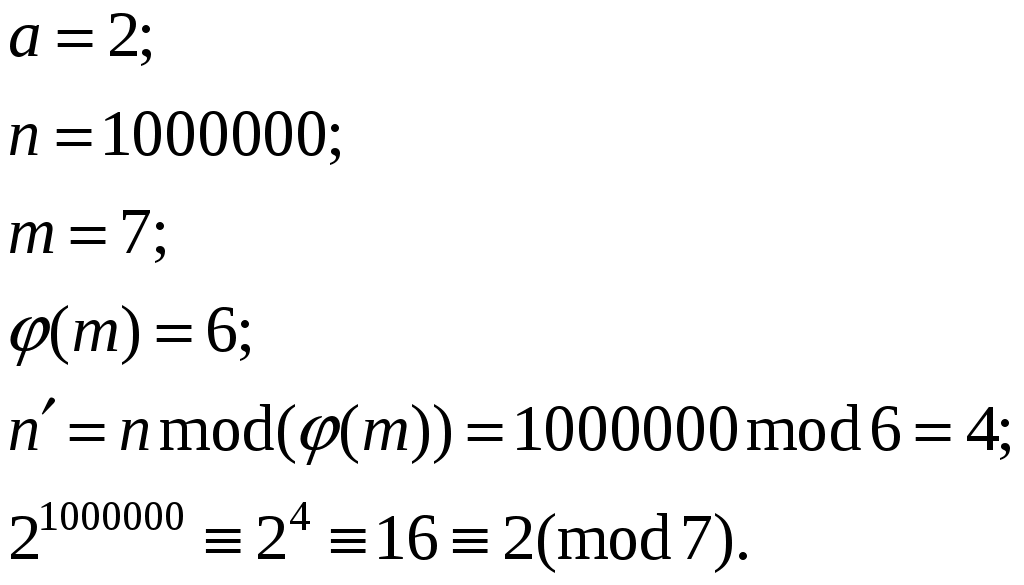
{ Расширенный алгоритм Евклида }
Упражнения для самоконтроля

1. 
   Решить систему сравнений:
   

2. 
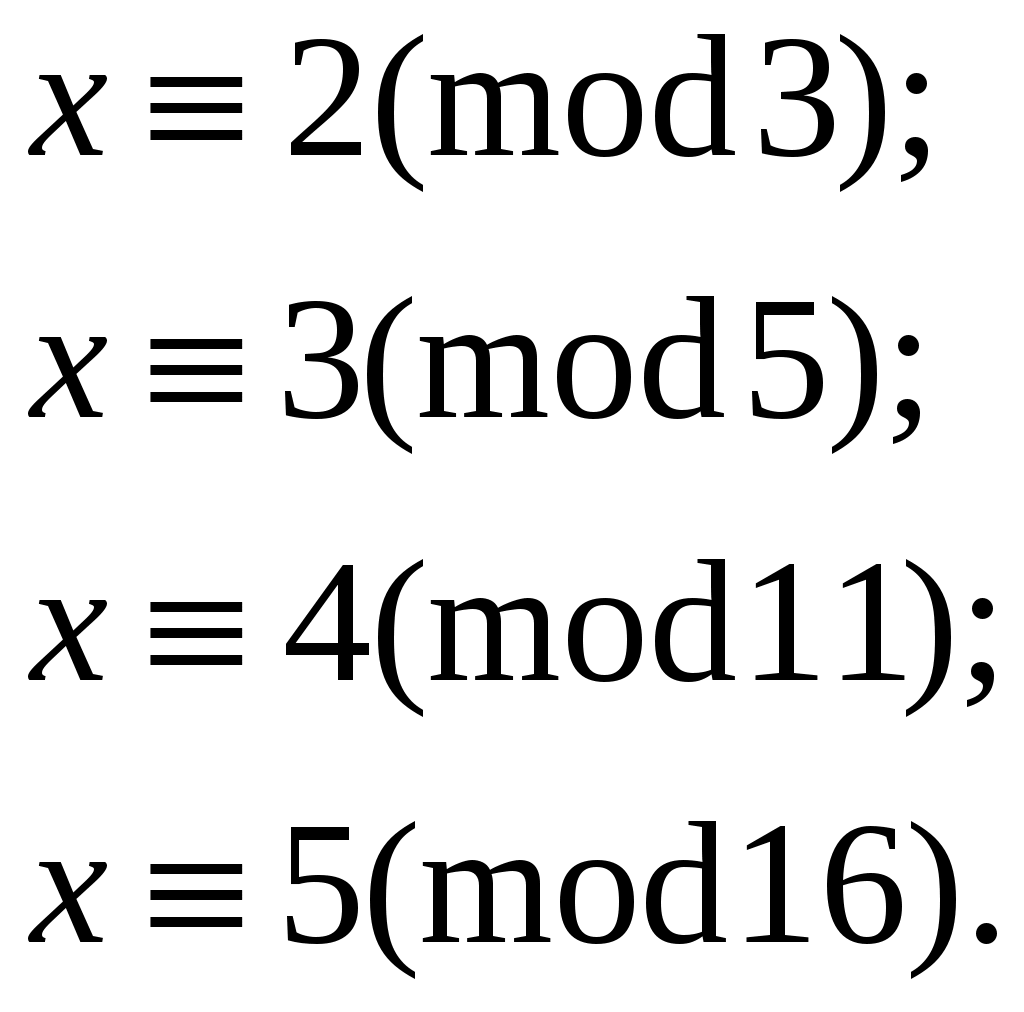
   Найти последнюю цифру в записи числа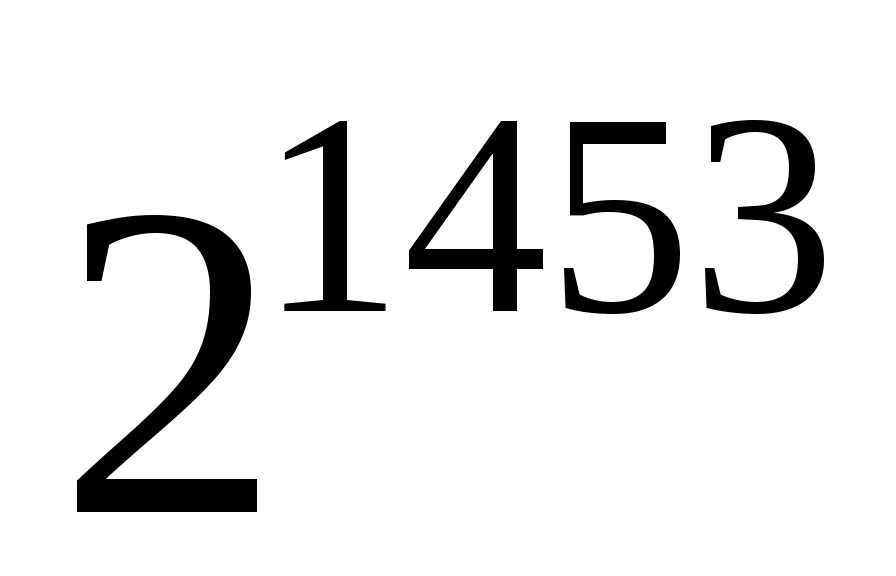 в системе счисления по основанию 11.
   
3. 
   Вычислить .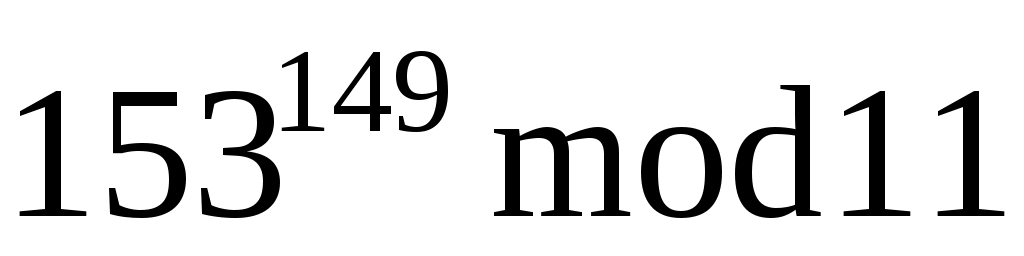
   
4. 
   Вычислить .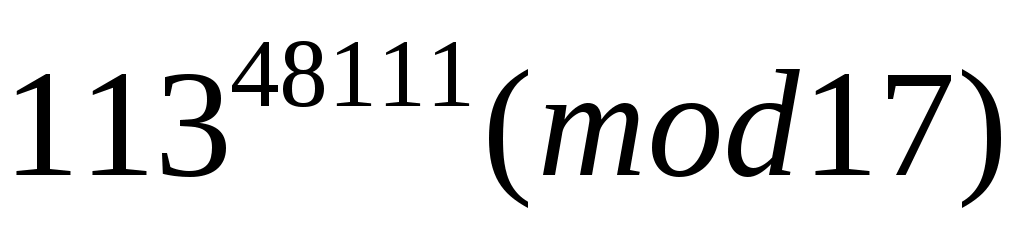
   

---