Файл: Программа работы.doc

Несложно показать [2-4], что для любого простого и некоторого

.

1.1.3 Расширенный метод Евклида

Рассмотрим теперь расширенный алгоритм Евклида, позволяющий наряду с наибольшим общим делителем чисел и находить натуральные числа и , удовлетворяющие равенству . От обычного алгоритма Евклида он отличается тем, что наряду с последовательностью остатков вычисляются ещё две вспомогательные последовательности и . Расширенный алгоритм Евклида заключается в следующем. Пусть , нам необходимо найти натуральные числа и , удовлетворяющие равенству . На первом шаге положим, что . Далее будем выполнять следующую последовательность действий, до тех пор пока :



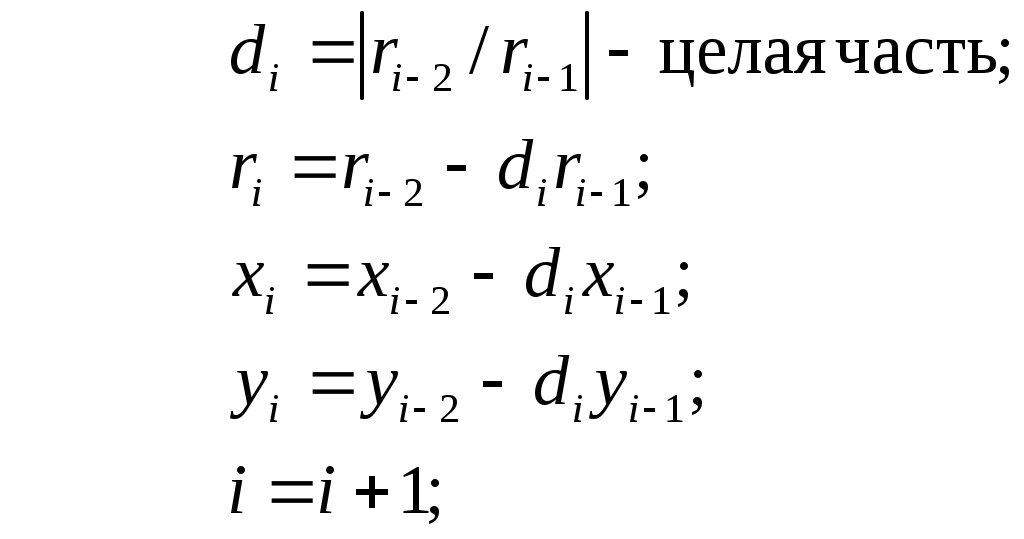
Значения и

---

, при которых , и будут искомыми в силу следующего утверждения:

Лемма. При всех , выполнимо равенство

Доказательство. Применим индукцию по . При равенство очевидно. Если равенства доказаны для всех значений индексов меньших , то для , пользуясь индуктивным предположением, получим

.

Легко видеть, что сложность данного алгоритма отличается от сложности обычного алгоритма Евклида не более, чем на константный сомножитель, и составляет , где длина записи чисел и .

Расширенный метод Евклида может применяться для нахождения корней частного случая диофантовых уравнений .

В криптографии расширенный метод очень часто применяется для нахождения обратного значения по модулю, подробнее будет рассмотрено в разделе 2.
Упражнения для самоконтроля

1. 
   Определить, сколько делителей имеет заданное число 945.
   
2. 
   Найти степени чисел 2, 3, 4, 5 точно делящие число 23455.
   
3. 
   Найти значение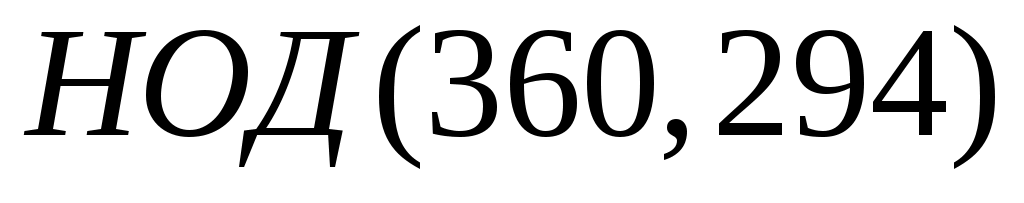 двумя способами: через разложение на простые множители и используя алгоритм Евклида.
   
4. 
   При помощи алгоритма Евклида найти наибольший общий делитель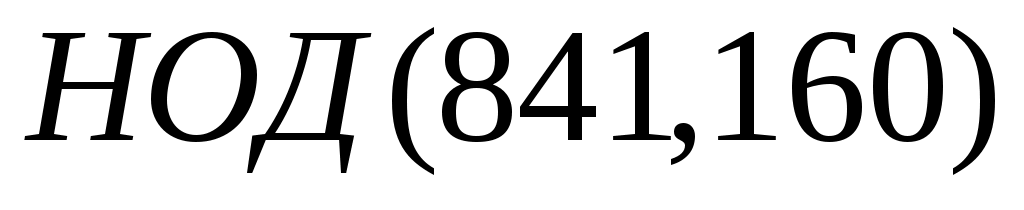 и представить его в виде линейной комбинации с целыми коэффициентами.
   
5. 
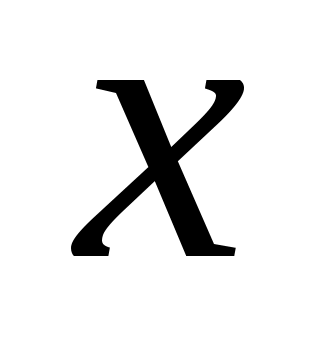   Найти и 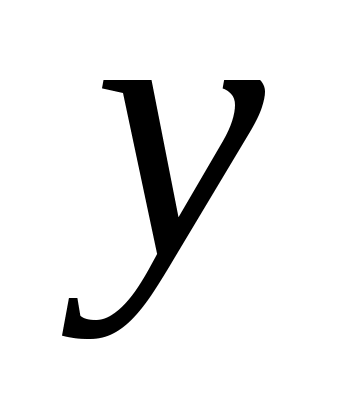из уравнения .
   

---

---

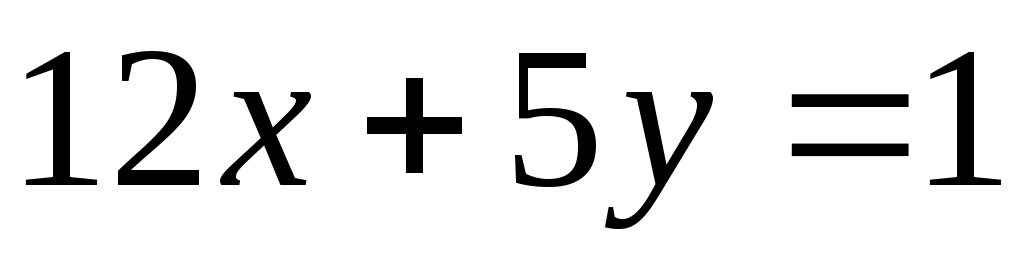1.2. СРАВНЕНИЯ

1.2.1. Отношение сравнимости

Определение 11. Для данных целых чисел , и , говорят, что сравнимо с по модулю , если разность делится на :

.

При этом число называется модулем сравнения.

Из определения 12 непосредственно следуют следующие свойства сравнений:

1. Рефлексивность:

.

2. Симметричность:

.

3. Транзитивность:

.

Таким образом, для фиксированного значения отношение сравнимости является отношением рефлексивным, симметричным и транзитивным, т.е. отношением эквивалентности.

В этих условиях каждый класс эквивалентности по этому отношению обладает в точности одним представителем в множестве чисел от

---

до [9-11]. Иными словами, любое целое число сравнимо по модулю ровно с одним числом в промежутке от до .

Множество классов эквивалентности по модулю (называемых классами вычетов) обозначается .

Несложно убедиться, что сравнения обладают следующим свойством [8].
4. Коммутативность

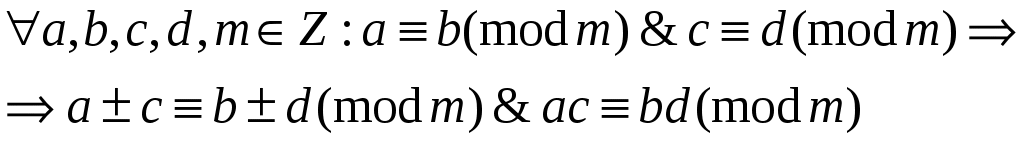Таким образом, множество является коммутативным кольцом, т.е. вычет по одному и тому же модулю можно складывать, вычитать и перемножать, и эти операции удовлетворяют обычным аксиомам ассоциативности, коммутативности, существования противоположного элемента и т.д.
Рассмотрим условия существования противоположного элемента.
Теорема 3. Для каждого целого существует единственное целое число , такое что произведение сравнимо с по модулю , тогда и только тогда, когда и − взаимно просты:

---