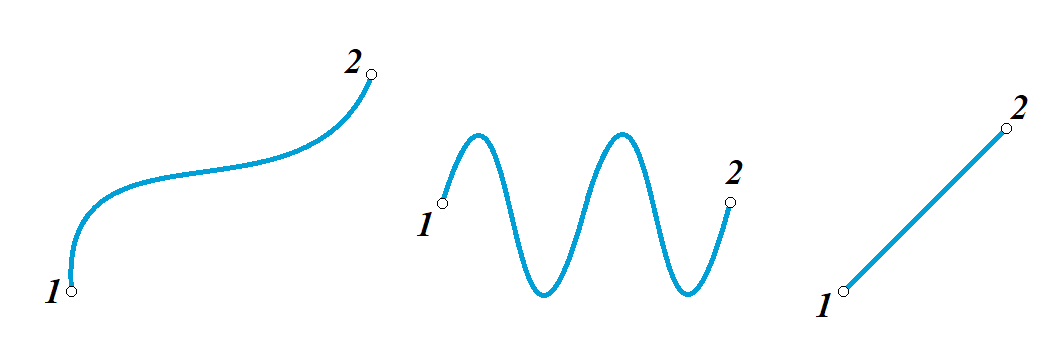
Путь, 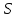– это длина всей траектории, вдоль которой происходил процесс движения предмета.

Перемещение, 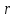– это отрезок, равный разности между конечной и начальной координатой предмета (отрезок, проведенный из начальной координаты в конечную, модуль [значение] перемещения равно длине этого отрезка).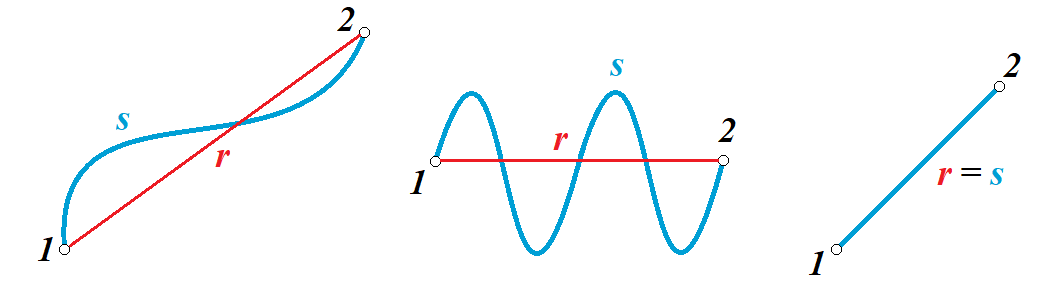



Представьте, что вы направляетесь в магазин, расположенный в 500 метрах от вас, а затем возвращаетесь обратно в исходное местоположение. Тогда ваш путь будет равен 1000 метров, а перемещение – нулю. Данный пример приведен для лучшего понимания различия в данных терминах.

Благодаря выше изложенному материалу, нам стало ясно, что для однозначного определения местоположения предмета необходимо задать его координату в некоторой системе координат. Тогда мы знаем, где оно находится (необходимо иметь ноль координат, относительно которого исчисляется координата предмета). Если предмет начинает движение, то для однозначного определения траектории движения (кривой, вдоль которой движется предмет), нам необходимо для каждой координаты знать момент времени, ей соответствующий. Тогда мы сможем построить зависимость координаты от времени. Затем, по такой зависимости мы сможем определить быстроту изменения координаты с течением времени (то есть определить скорость). Если же скорость предмета меняется по величине с течением времени, то такой предмет обладает тангенциальным ускорением (в случае, если ускорение постоянно – движение может быть либо равноускоренным, либо равнозамедленным; если же тангенциальное ускорение переменное – движение будет называться ускоренным, и наконец, если скорость предмета не меняется, то такое движение называется равномерным, а тангенциальное ускорение будет равно нулю). Однако, стоит добавить, что если вектор скорости меняет направление в процессе движение, то предмет обладает также нормальным ускорением.

Рассмотрим несколько примеров.

Пример 1. Проанализируем уравнение координаты, зависящей от времени следующим образом:

---

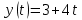
Для наглядности, построим график этой функции:

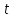	0	1
	3	7

График функции координаты от времени будет иметь вид:



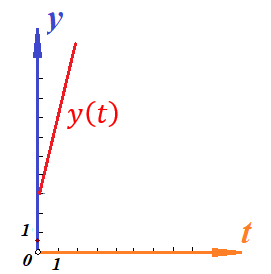
Определим величину скорости, как мы делали это выше:



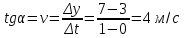
Угол наклона функции координат – постоянный, следовательно, постоянна и скорость. Тогда уравнение скорости будет иметь вид:



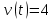
Построим график зависимости скорости от времен:



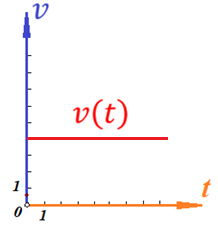
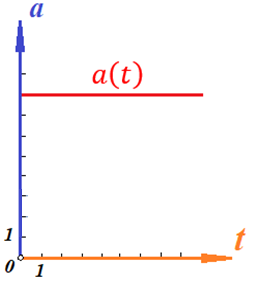
Поскольку скорость предмета не изменяется по величине, то тангенциальное ускорение равно нулю. Тогда график зависимости тангенциального ускорения от времени будет иметь вид:



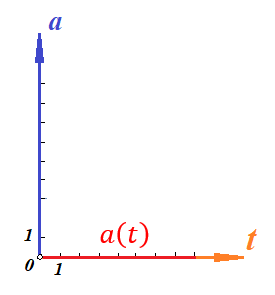
Нормальным ускорением предмет обладать не будет, поскольку движется строго по прямой.

Пример 2. Проанализируем уравнение координаты предмета, зависящее от времени следующим образом:



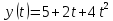
Для наглядности, построим график этой функции:

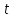	0	1	2	3	4
	5	11	25	47	77

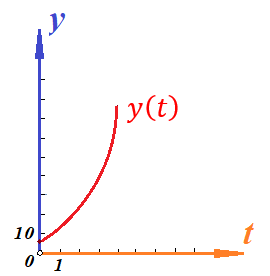
Для того, чтобы определить зависимость скорости от времени для данной зависимости координаты от времени, мы уже не можем воспользоваться определением тангенса угла наклона функции, поскольку угол все время меняется.

---

В полноценном курсе физике в таком случае применяют производную, однако, нам изучать ее необходимости нет.

Поэтому, пришло время привести уравнения, с помощью которых можно решить большинство кинематических задач. Их всего два, и применяются они только для равномерного и равноускоренного (равнозамедленного) движений!

Первое уравнение есть уравнение координаты:



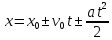
– координата предмета в момент времени ;

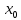– начальная координата предмета;

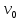– начальная скорость предмета;

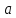– ускорение предмета (для квадратичной зависимости координаты от времени ускорение будет постоянным [это было рассмотрено выше], а для линейной зависимости координаты от времени– то есть для равномерного движения – равно нулю).

В простейшем случае – знак + соответствует равноускоренному движению, знак «-» - замедленному. Более подробно этот нюанс будет рассмотрен позже в примерах.

Второе уравнение – уравнение скорости:



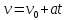
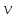– скорость предмета в момент времени .

Возвратимся к решению задачи. С помощью полученных сведений об уравнениях кинематики, «соберем» уравнение скорости:



Сопоставляя данную зависимость координаты от времени, можно понять, что:







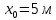
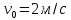
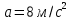
Ускорение в исходном уравнении координаты стоит с множителем ½, однако данный множитель отсутствует в заданном для анализа уравнении, следовательно, записав уравнение 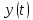в «общем виде», получим:

---

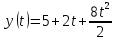
Тогда, согласно исходному уравнению скорости:



Для рассматриваемого получим: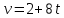



Для наглядности, построим график этой функции:

	0	1
	2	8

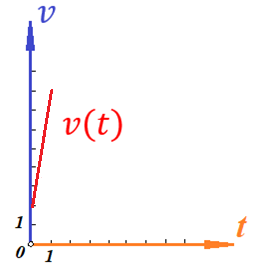
Поскольку зависимость скорости от времени – линейная, то угол наклона функции скорости всюду одинаков, т.е. ускорение предмета будет постоянным.





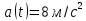
Пример 3. Дана зависимость координаты от времени 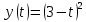. Определить путь, перемещение, среднюю скорость пути, среднюю скорость перемещения предмета, движущегося согласно этому уравнению за время от 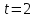до .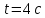

Для того, чтобы определить перемещение, необходимо знать, где предмет находился в начальный и конечный моменты времени. Подставим заданные моменты времени в уравнение и получим значения координат предмета:



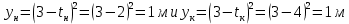
То есть, предмет вернулся в координату, с которой начал движение, из этого следует, что его перемещение равно нулю, т.е.:

---

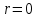
Таким образом, мы понимаем, что предмет в процессе движения останавливается в некоторой координате и затем поворачивает назад.

Как найти момент времени, когда предмет поворачивает?

Для этого необходимо получить уравнение скорости и приравнять его к нулю, поскольку именно в точке поворота скорость предмета обращается в ноль, а затем меняет свое направление.

Имеем:



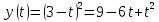
Тогда получим:



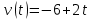
В точке поворота:



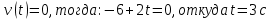
То есть, предмет поворачивает в третью секунду своего движения.

Теперь определим путь. Для этого необходимо знать, в какой координате находился предмет в момент времени 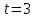с. Имеем: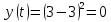



То есть, координаты предмета и соответствующие этим координатам моменты времени есть:







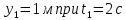
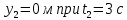
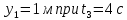
Очевидно, что путь равен 2 м.

Теперь приступим к определению средней путевой и средней скорости перемещения. По определению, средней скоростью называется весь путь, пройденный предметом, деленный на время, за который этот путь был пройден:



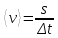
Тогда средняя путевая скорость:



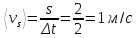
Поскольку предмет двигался

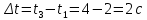
А средняя скорость перемещения:



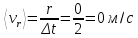
Пример 4. Рассмотрим еще одну задачу на определение перемещения и пути предмета за определенное время движения. Дана зависимость координаты от времени: 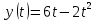. Задача стоит та же – определить перемещение и путь предмета с момента времени

---

Смотрите также файлы

• Задание Что лежит в основе действующего финансового устройства России Задание 3.docx

• Учебнопрактическое пособие по ознакомлению с окружающим миром разработано для детей дошкольного возраста. В пособии имеются подробные конспекты по ознакомлению с окружающим миром для средней группы доу. (45 лет).docx

• Задание Проведите анализ планов и организации досуговых мероприятий различной направленности в организациях дополнительного образования.docx

• 4. Начало и первый этап Английской революции 16401642гг.odt

• Отчет по производственной практике по профессиональному модулю пм. 01 Ввод и обработка цифровой информации.pptx