Файл: Кафедра математики и методики обучения математике методика обучения учащихся тождественным преобразованиям рациональных выражений.docx
Добавлен: 19.03.2024
Просмотров: 274
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Пример рациональных выражений: 8, 54 + х,
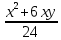 .
.Целые рациональные выражения не содержат в знаменателе дроби переменную, т. е. приведённые выше примеры отражают целые рациональные выражения.
Целыми выражениями называют такие выражения, в состав которых входят числа и переменные, операции сложения, вычитания, умножения и деления на число, не равное нулю, но не содержащие деления на переменные и извлечения корня (возведения в степень с дробным показателем, в частности).
Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.
Множество всех допустимых значениях переменных называют областью определения алгебраического выражения.
Целое выражение имеет смысл при любых значениях входящих в него переменных, так как для нахождения значения целого выражения нужно выполнить действия, которые всегда возможны [15].
Приведём примеры:
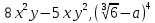
-
Дробные рациональные выражения
Выражение вида –
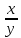 называется дробью.
называется дробью.Дробь, у которой числитель и знаменатель являются многочленами, называют рациональной дробью.
В этой части мы рассмотрим дробные выражения.
Дробные выражения отличаются от целых тем, что они содержат деление на выражение с переменными.
Примеры дробных выражений:
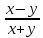 ;
; 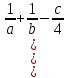 .
. Объединением множеств целых и дробных выражений является множество рациональных выражений.
Если в рациональном выражении заменить переменные числами, то получим числовое выражение. Однако эта замена возможна только тогда, когда она не приводит к делению на нуль.
Дробное выражение при некоторых значениях переменных может не иметь смысла [12].
Приведём примеры.
-
Выражение 24 +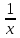 — не имеет смысла при
— не имеет смысла при  = 0. При всех остальных значениях
= 0. При всех остальных значениях  , это выражение имеет смысл.
, это выражение имеет смысл. -
Выражение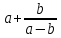 +
+  имеет смысл при тех значениях
имеет смысл при тех значениях 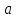 и
и 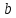 , когда
, когда 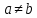 .
.
В рациональной дроби допустимыми считаются те значения переменных, при которых не обращается в нуль знаменатель дроби.
Например, выражение
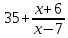 при
при  = 7 не имеет смысла, потому что числового значения этого выражения при
= 7 не имеет смысла, потому что числового значения этого выражения при  = 7 не существует. При всех других значениях a это выражение имеет смысл.
= 7 не существует. При всех других значениях a это выражение имеет смысл. В рассмотренном выше примере областью определения выражения является множество всех чисел, кроме
 = 7 .
= 7 . Подмножеством множества рациональных выражений является множество рациональных дробей. Это дроби, числителями и знаменателями которых являются многочлены. Поэтому рациональные выражения
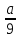 ;
;  ;
;  ;
; 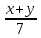 являются примерами рациональных дробей.
являются примерами рациональных дробей. Рациональная дробь может быть, как целым выражением, так и дробным. Знаменатель рациональной дроби не может быть нулевым многочленом, т. е. многочленом, тождественно равным нулю.
Рассмотрим основное свойство рациональной дроби.
Равенство 8
 − 3 + 7
− 3 + 7 + 12 = 15
+ 12 = 15 + 9 является тождеством, так как оно выполняется при любых значениях
+ 9 является тождеством, так как оно выполняется при любых значениях 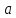 .
. Равенство
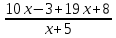 =
=  также естественно считать тождеством, однако, при
также естественно считать тождеством, однако, при  = −5 рациональные дроби, которые входят в данное равенство, не имеют числового значения.
= −5 рациональные дроби, которые входят в данное равенство, не имеют числового значения.Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получим дробь тождественно равную данной.
Данное свойство является основным для рациональной дроби, его запись ведётся таким образом:
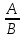
=

Где А, В, С – многочлены, при этом многочлены В и С ненулевые.
Согласно этому свойству выражение
 можно заменить на тождественно равную дробь
можно заменить на тождественно равную дробь 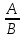 . Такое тождественное преобразование называют сокращением дроби на множитель C.
. Такое тождественное преобразование называют сокращением дроби на множитель C.Из основного свойства дроби следует, что
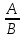 =
= 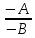 и
и 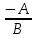 =
= 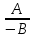 .
.Каждую из дробей
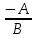 и
и 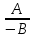 можно записать в виде выражения
можно записать в виде выражения 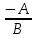 , то есть
, то есть 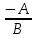 =
= 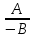 =
= 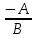 .
.- 1 2 3 4 5 6
мЕТОДИКА ОБУЧЕНИЯ УЧАЩИХСЯ ТОЖДЕСТВЕННЫМ ПРЕОБРАЗОВАНИЯМ РАЦИОНАЛЬНЫХ ВЫРАЖЕНИЙ
-
Различные трактовки понятия тождества. Виды тождественных преобразований
Тождественные преобразования предполагают собой работу, которая проводится с числовыми и буквенными выражениями, а также с выражениями, содержащими переменные. Все эти преобразования производятся для того, чтобы привести исходное выражение к такому виду, который будет удобным для решения задачи. Основные виды тождественных преобразований мы рассмотрим в этой главе.
Впервые учащиеся встречаются с понятием тождественных преобразований на уроках алгебры в 7 классе. Впервые вводится понятие тождественно равных выражений.
Тождественное преобразование выражения – это действия, выполняемые с целью замены исходного выражения на выражение, которое будет тождественно равным исходному выражению [16].
Посмотрим на наглядном примере:
Используем для замены выражения
 тождественно равное ему выражение
тождественно равное ему выражение 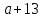 и проведём тождественное преобразование выражения
и проведём тождественное преобразование выражения  .
.Рассмотрим форму записи выражений при проведении тождественных преобразований.
Обыденная запись исходного и полученного в ходе преобразования выражения в виде равенства. Запись
 =
= 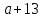 означает, что выражение
означает, что выражение было приведено к виду
было приведено к виду 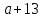 .
. Последовательное выполнение действий приводит нас к цепочке равенств, которая состоит из нескольких расположенных по порядку тождественных преобразований.
Запись
 =
= 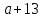 = 13 +
= 13 + 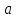
Мы наблюдаем последовательное проведение двух преобразований: в первую очередь выражение
 привели к виду
привели к виду 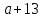 , а затем – к виду 13 +
, а затем – к виду 13 + 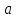 .
.Ряд выражений, которые мы начинаем изучать в 8 классе, имеют смысл не при всех значениях переменных. Проведение тождественных преобразований в этих случаях требует от нас внимания к области допустимых значений переменных (ОДЗ). Выполнение тождественных преобразований может оставлять ОДЗ постоянной или же сужать ее.
Сужение либо расширение области допустимых значений переменных во время выполнения тождественных преобразований имеет общее значение при решении задач, так как может воздействовать на точность проведения вычислений и привести к возникновению ошибок.
Выделим виды тождественных преобразований, с которыми учащимся приходится встречаться чаще всего, в группу основных тождественных преобразований. Также помимо основных тождественных преобразований существует ряд преобразований, которые относятся к выражениям конкретного вида. Для дробей – это приемы сокращения и приведения к новому знаменателю. Для выражений с корнями и степенями - это все действия, выполненные на базе свойств корней и степеней. Для логарифмических выражений действия, проводимые на основе свойств логарифмов. Для тригонометрических выражений все действия, в которых использованы тригонометрические формулы [3].
Рассмотрим основные тождественные преобразования.
-
Перестановка местами слагаемых, множителей.
В первую очередь рассмотрим перестановку местами слагаемых. С этим тождественным преобразованием учащиеся встречаются чаще всего. Основное правило: в любой сумме перестановка слагаемых местами не отражается на результате. Данное правило сформировано на переместительном и сочетательном законах сложения. Эти свойства дают возможность нам переставлять слагаемые местами и получать при этом выражения, тождественно равные исходным. Именно поэтому перестановка слагаемых местами в сумме является тождественным преобразованием.
В качестве слагаемых в сумме могут выступать не только числа, но и выражения. Их точно так же, как и числа, можно переставлять местами, не влияя на конечный результат вычислений.


