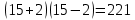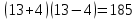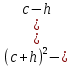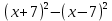Файл: Кафедра математики и методики обучения математике методика обучения учащихся тождественным преобразованиям рациональных выражений.docx

Цикл упражнений описан объединенными в последовательность упражнениями нескольких аспектов изучения и приемов распределения материала.

Цикл упражнений связан с изучением одного тождества, вокруг которого группируются другие тождества, находящиеся с ним в естественной связи. В состав цикла вместе с исполнительными заданиями входят и те, которые требуют распознавания применимости рассматриваемого тождества. Изучаемое тождество применяется для проведения вычислений на различных числовых областях. Учитывается специфика тождества; в частности, организуются связанные с ним обороты речи.

Задания в каждом цикле разбиты на две группы. К первой группе относятся те задания, выполняемые при первоначальном знакомстве с тождеством, которые служат учебным материалом для нескольких последующих уроков, объединенных одной темой.

Вторая группа упражнений связывает изучаемое тождество с различными приложениями. Эта группа не образует композиционного единства – упражнения здесь разбросаны по различным темам.

Описанная структура цикла входит в этап по формированию навыков использования конкретных видов преобразований. На заключительном этапе – этапе синтеза циклы видоизменяются. В первую очередь происходит объединение обоих групп заданий, которые образуют «развернутый» цикл, причем из первой группы исключаются наиболее простые по формулировкам или по сложности выполнения задания. Оставшиеся типы заданий усложняются. Затем происходит слияние циклов, относящихся к различным тождествам, в силу чего повышается роль действий по распознаванию применимости того или иного тождества [2].

Особенности циклов заданий, связанных с тождествами для элементарных функций, обоснованы тем, что соответствующие тождества изучаются в связи с изучением функционального материала, а также они появляются позже тождеств первой группы и изучаются с применением уже сформированных навыков проведения тождественных преобразований.

Любая новая элементарная функция резко расширяет область чисел, обозначенных и названных индивидуально. Поэтому в первую группу заданий циклов должны войти задания на установление связи этих новых числовых областей с исходной областью рациональных чисел.

Большая часть, в которой используются тождественные преобразования, связанные с элементарными функциями, приходится на решение иррациональных и трансцендентных уравнений. В циклы,

относящиеся к усвоению тождеств, входят только наиболее простые уравнения, в данном случае целесообразно проводить работу по усвоению приема решения таких уравнений: сведение его путем замены неизвестного к алгебраическому уравнению.

Немалая часть тождеств, изучаемых в курсах алгебры и начал анализа, доказывается в них, или поясняется. Эта сторона изучения тождеств имеет большое значение для обоих курсов, так как доказательные рассуждения в них с наибольшей четкостью и строгостью проводятся именно по отношению к тождествам. Вне этого материала доказательства обычно менее полны, они не всегда выделяются из состава применяемых средств обоснования.

В качестве основы для построения доказательства тождеств, используются свойства арифметических операций.

Воспитательное воздействие вычислений и тождественных преобразований нацелено на развитие логического мышления, если от учащихся будут систематически требоваться обоснования вычислений и тождественных преобразований, на развитие функционального мышления, что достигается различными путями. Значение вычислений и тождественных преобразований играет огромную роль в развитии воли, памяти, сообразительности, самоконтроля, творческой инициативы учащихся.

Запросы бытовой, производственной вычислительной практики требуют формирования у учащихся прочных, автоматизированных навыков рациональных вычислений и тождественных преобразований. Эти навыки вырабатываются в ходе любой вычислительной работы, тем не менее, необходимы особые тренировочные упражнения в быстрых вычислениях и преобразованиях [7].

Для того, чтобы доказать тождественность двух выражений, практически использовать понятие тождественных выражений невозможно. Учащимся необходимо понимать, что сущность тождественных преобразований состоит в применении к выражению определений и свойств тех действий, которые прописаны в выражении, или в прибавлении к нему выражения, тождественно равного нулю, или в умножении его на выражение, тождественно равное единице. В последствии усвоения данных положений, учащиеся достаточно часто не могут понять

, почему указанные преобразования позволяют утверждать, что исходное выражение и полученное являются тождественными, то есть принимают одинаковые значения при любых системах значений переменных. Необходимо, чтобы учащиеся понимали, что такие выводы тождественных преобразований являются следствиями определений и свойств соответствующих действий.

Аппарат тождественных преобразований, накопленный в предшествующие годы, расширяется [3].

Для более подробного анализа этого вопроса проанализируем наиболее востребованные учебники алгебры за 7 класс: авторов Г.В. Дорофеева и А.Г. Мерзляка.

В учебнике А.Г. Мерзляка первыми вводятся понятия алгебраических выражений, их классификация и отмечается, что в 7 классе учащиеся будут работать только с целыми выражениями. Одна из глав посвящена работе по упрощению выражений, знакомству с формулами и приёмами по преобразованию выражений, а также умению классифицировать алгебраические выражения.

В учебнике Г.В. Дорофеева к изучению выражений немного другой подход, перед ними стоит ещё две большие темы: дроби и проценты, прямая и обратная пропорциональность. Авторы этого учебника нацелены на рассуждения детей, т.е. развитию самостоятельности, например, одно из первых заданий это рассуждение о приёме, который нам необходимо применить, чтобы упростить выражение.

1 2 3 4 5 6

Типичные ошибки учащихся при работе с тождественными преобразованиями и рекомендации по их устранению

Раздел «Тождественные преобразования» занимает основное место в школьном курсе математики. Изучение тождественных преобразований

имеет самостоятельное значение, т.к. связан со следующими вопросами:
1. обобщение операций над числами, проведение вычислений «в общем виде», обучение применению алгебраической символики;
2. классификация и определение алгебраических выражений, преобразование выражений к стандартному виду;
3. рационализация выражений.
тождественные преобразования играют роль вспомогательного «инструмента» при решении уравнений и неравенств, при исследовании функций и ряде других тем школьного курса математики.
тождественные преобразования имеют значимое воспитательное значение, т.к. они способствуют развитию у учащихся операционного мышления, воспитанию таких качеств личности, как целеустремленность в поиске решения, сообразительность, аккуратность, честность, справедливость.

Самая типичная ошибка учащихся состоит в том, что они при решении уравнений и неравенств без дополнительных пояснений используют преобразования, которые нарушают равносильность, приводящую к потере или появлению корней. Значимая группа ошибок заключается в том, что учащиеся не уделяют должного внимания нахождению области определения выражений, хотя конкретно она в ряде случаев есть ключ к решению.

Разнообразие тождественных преобразований усложняет понимание цели, которая является конечной при работе с выражениями. Неточное понимание целевого преобразования отрицательно отражается на осознании предназначения и служит источником множественных ошибок. Этот факт указывает на то, что педагогу необходимо включать разъяснение конкретных целей при выполнении всех тождественных преобразований, что является составной частью методики обучения.

Для управления этим процессом преподаватель обязан уметь давать чёткие характеристики сущности допущенных учащимися ошибок. Наличие точности помогает учащимся найти подходящие действия для дальнейшей работы по осуществлению тождественных преобразований выражений [6].

Типичные ошибки учащихся при работе с тождественными преобразованиями:

Смешивают правила умножения степеней с правилом возведения в степень ( ).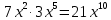
Распространяют по неверной аналогии правила умножения степеней с одним основанием на случай умножения степеней с разными основаниями ( ).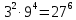
Складывают показатели степеней при сложении степеней – смешивают с правилом умножения степеней ( ).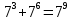
Неправильно применяют формулы (по неверной аналогии: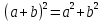 или 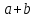lg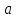 ( )= lg +lg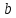 , или ).
Сокращают в алгебраической дроби по неверной аналогии не множители, а слагаемые ( = ).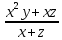
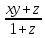Изменяют знак не у всех членов вычитаемого, когда вычитается многочлен и, тем более дробь.
Не учитывают знак подкоренного выражения при использовании свойства арифметического корня и получают под корнем отрицательное число.

Одним из типов ошибок является неправильное применение формул, составим ряд упражнений для того, чтобы в дальнейшем была возможность исключить эти ошибки.