Файл: Кафедра математики и методики обучения математике методика обучения учащихся тождественным преобразованиям рациональных выражений.docx

Замеченные недостатки первого определения не найдены во втором.

Приведём пояснительные примеры:

1. 
   lga + lgb = lg (ab)
   
2. 
   - =0
   

Этому определению удовлетворяют приведённые примеры, в отличие от первого определения, но существует ряд недостатков.

Главной ценностью тождеств является возможность заменять одно выражение другим, при условии того, что они тождественны, а по второму определению вытекает, что равенства 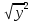= 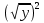и 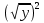=у – тождества, а вот равенство 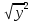= у не будет являться тождеством.

Используя многие неравенства, которые являются тождествами, по второму определению, можно привести решение уравнения к неравносильному решению.

3. 
   Равенство, верное при любых значениях переменной (пар значений переменных, троек значений переменных и т. д.), принадлежащих данному множеству, называется тождеством на этом множестве.
   

Замена одно выражение другим, тождественно равным ему на данном множестве, называют тождественным преобразованием этого выражения на указанном множестве.

Это определение является наиболее точным и не имеет недостатков, можно прийти к выводу, что при решении заданий имеет место обращения именно к этому определению.

Каждая область знаний, в которой используются математические данные, испытывает время от времени потребность в упрощении методов решений заданий, и использует замену одного выражения другим как вынужденную меру для упрощения, т.е. используется метод тождественных преобразований [3].

Начальные знания о тождественных преобразованиях выражений учащиеся получают в начальной школе, а углубленное и систематизированное изучение этого вопроса начинается в 7 классе основной школы в программе изучения курса алгебры.

В 7 классе учащиеся получают полноценное представление о целых рациональных выражениях (одночленах и многочленах). В 8 классе учащиеся изучают дробные выражения (дробные рациональные выражения, арифметические квадратные корни). В 9 и 10 классах учащиеся получают представление об иррациональных выражениях (степени с

---

рациональными показателями, корни n-ной степени). 10 класс знакомит детей с тригонометрическими выражениями, а 11 с логарифмическими.

Заменяя одно выражение на более удобное или более простое, мы находим решение задачи, то есть требуется провести тождественные преобразования выражений и упростить решение.

2. 1   2   3   4   5   6

---

Выражения и их виды

В течение всего курса математики учащиеся многократно встречаются с выражениями и учатся работать с различными их видами. Выражения, которые содержат операции сложения, вычитания, умножения, деления, извлечением квадратного корня, возведение в степень, возведения в степень с дробными показателями, знаками логарифма, знаками косинуса.

Алгебраические выражения включают в себя только те выражения, которые содержат такие действия над переменными, как сложение, вычитание, умножение, деление, извлечение корня, возведение в степень с рациональным показателем.

Алгебраические выражения включают в себя два класса:

1. 
   рациональные, включают в себя только те выражения, в которых выполняются действия сложения, вычитания, умножения, деления, возведения в целую степень;
   
2. 
   иррациональные, включают в себя только те выражения, в которых выполняются действия по извлечению корня, возведению в степень с дробным показателем.
   

Также рациональные выражения можно разбить на два класса:

1. 
   множество целых выражений, которые включают только те выражения, в которых не содержится деление на выражение с переменными;
   
2. 
   множество дробных выражений, которые включают только те выражения, в которых содержится деление на выражение с переменными в степень с отрицательными показателями.
   

В ходе обучения школьной программы также рассматриваются неалгебраические выражения, в которых содержатся переменные под знаками lg, sin, cos, tg, со знаком модуля, с операциями возведения в степень с иррациональными показателями.

Необходимо отметить, что выражения lg 2, sin 1 даже при наличии знаков логарифма и синуса являются алгебраическими, потому что под ними находятся не переменные, а числа.

Основная программа формирования умений и навыков при выполнении тождественных преобразований выражений приходится на курс алгебры, начиная с 7 класса основной школы. Это зависит от увеличения чисел и расширения знаний о совершаемых преобразованиях, с усложнением действий по обоснованию и выяснению критерий их применения, с выделением и исследованием обобщенных понятий тождества, равносильного преобразования,

---

тождественного преобразования, логического следования [1].

Этапы освоения применения преобразований формул и буквенно-числовых выражений.

1. 
   Начала алгебры. Этап характерен использованием нерасчлененной системы преобразований; она представлена правилами выполнения действий над одной или обеими частями формулы.
   

Рассмотрим на примере.

Решить уравнение: а) 7х − 3х =4

Упростим уравнение, воспользовавшись распределительным законом

7х − 3х = (7 − 3)х.

Основанное на этом a тождестве тождественное преобразование переводит данное уравнение в равносильное ему уравнение 4х = 4

Главная мысль решения лежит в упрощении данных формул с использованием нескольких правил.

На данном этапе продолжается формирование навыков применения конкретных видов преобразований. Система правил и способов проведения преобразований имеет очень широкую область приложений, то есть исследуется на протяжении всего курса математики и используется на этапе начал алгебры. Впрочем, данная система нуждается в дополнительных преобразованиях, которые предусматривают особенности структуры преобразуемых выражений. С введения формул сокращенного умножения наступает освоение соответствующих видов преобразований. Далее рассматриваются преобразования, которые связанны с операцией возведения в степень, а также с различными классами элементарных функций – степенных, показательных, тригонометрических, логарифмических. Каждый из этих типов преобразований должен пройти этап изучения, на котором концентрируется внимание на освоении их отличительных особенностей.

По мере накопления материала возникает возможность на базе выделения общих особенностей рассматриваемых преобразований ввести понятия тождественного равносильного преобразований.

Преобразования разделяют на два класса: тождественные преобразования как преобразования выражений и равносильные преобразования как преобразования формул. В случае, если появляется потребность упростить одну часть формулы, то в ней выделяется выражение, которое и служит аргументом для применяемого тождественного преобразования. Соответствующий предикат при этом считается постоянным [8].

2. 
   Организация целостной системы преобразований (синтез).
   

---

Основной целью данного этапа, считается составление гибкого и мощного аппарата, который будет пригоден для применения в решении различных учебных заданий. Второй этап исследования преобразований разворачивается на протяжении всего курса алгебры неполной средней школы. Переход к третьему этапу происходит при итоговом повторении курса в процессе осмысления уже усвоенного по частям материала, по отдельным типам преобразований.

3. 
   Целостная система преобразований в курсе алгебры и начал анализа, не прекращает постепенное улучшение, когда основные черты уже сформированы. К уже изученным видам преобразований прибавляются новые, относящиеся к тригонометрическим функциям, дополняющие её структуру. Обязательно упоминание о специфическом виде преобразования выражений, которые основываются на правилах дифференцирования и интегрирования; выражений, содержащих предельные переходы, и преобразования.
   

Основным отличием между алгебраическими и аналитическими выражениями можно назвать различие в характере множества, которые проходят переменные в тождествах. В алгебраических тождествах переменные пробегают числовые области, а в аналитических тождествах этими множествами являются определенные множества функций. Наиболее чётко это прослеживается на простейшем примере формулы, выражающей правило дифференцирования суммы: 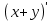= ; где x и y – переменные, которые пробегают множество дифференцируемых функций с общей областью определения. Не обращая внимания на то, что отмеченное различие не фиксируется в обучении в курсе алгебры и начала анализа, практика демонстрирует, что рассматриваемые преобразования усваиваются довольно уверенно; этому способствует их внешнее сходство с преобразованиями алгебраического типа [8].

3. 
   Целые рациональные выражения
   

Рациональным выражением является выражение, в котором, относительно входящих в него переменных и чисел, не выполняется никаких других операций помимо операций сложения, вычитания, умножения, деления и возведения в целую степень.

Рациональные выражения – это целые и дробные выражения.

---