Файл: Федеральное агенство по образованию рф гоу впо бурятский государственный университет.doc
Добавлен: 27.04.2024
Просмотров: 65
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
На основе спектров поглощения были построены кривые зависимости оптической плотности от рН при различных длинах волн (рис.2), выбранных по методу Адамовича [29].
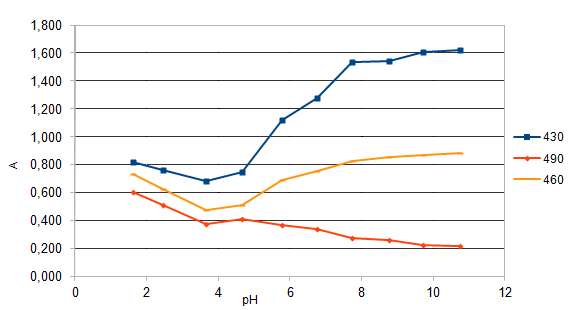
Рис.2. Зависимость оптической плотности ПАР от рН
при различных длинах волн
(СПАР = 5*10-5 моль/ дм3, l=10мм)
Исходя из этих кривых были рассчитаны константы диссоциации реагента по методу Комаря [29].
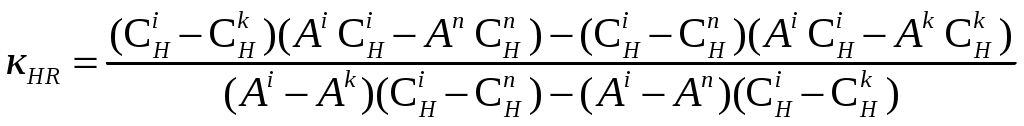
Где i,n,k – номера опытов;
СН — равновесные концентрации ионов водорода;
Аi,Аn,Аk —соответствующие им оптические плотности.
Результаты приведены в таблице 5. Константы диссоциации соответствуют следующим равновесным (учитывая что в сильнокислой области реагент находится в протонированной форме H4R2+):
H4R2+↔ H++H3R+ K4=[H3R+][H+]/[ H4R2+]
H3R+↔ H++H2R K5=[H2R][H+]/[ H3R+]
H2R↔ H++HR- K6=[HR-][H+]/[ H2R]
HR-↔ H++R2- K7=[R2-][H+]/[ HR-]
Таблица 5
Константы диссоциации ПАР
| | К1 | К2 | К3 | К4 |
| 1 | 3,60*10-3 | 1,13*10-6 | 3,20*10-7 | 6,90*10-10 |
| 2 | 2,80*10-3 | 3,48*10-6 | 5,30*10-7 | 7,10*10-10 |
| 3 | 2,60*10-3 | 1,29*10-6 | 4,70*10-7 | 8,40*10-10 |
| | 3,00*10-3 | 1,97*10-6 | 4,40*10-7 | 7,47*10-10 |
Так как одной из задач было исследование механизма комплексообразования железа с ПАР, необходимо было выяснить формы существования реагента в определенных областях рН. Для
этого с использованием полученных констант, было рассчитано процентное содержание форм реагента при различных рН среды.
В
растворе ПАР существует в виде всех возможных форм, тогда общая аналитическая концентрация равна:
Р
 асчет равновесной концентрации каждой из форм осуществлялся по формулам:
асчет равновесной концентрации каждой из форм осуществлялся по формулам:где СR=5∙10-4М
Данный расчет позволил рассчитать доли каждой формы:
α=Сравн./Сан.∙100%,
где Сравн.- равновесная концентрация определяемой формы;
Сан.-общая аналитическая концентрация реагента
Процентное содержание форм ПАР в зависимости от рН представлены в табл. 6, а их графическая интерпретация на рис. 3.
Таблица 6
Процентное содержание форм реагента при различных рН
| рН α,% | α, % | Σ,% | ||||
| [H4R2+] | [H3R+] | [H2R] | [HR-] | [R2-] | | |
| 1,62 | 99,89 | 0,11 | | | | 100 |
| 2,45 | 98,90 | 1,10 | | | | 100 |
| 3,65 | 90,03 | 9,97 | | | | 100 |
| 4,65 | 47,43 | 52,54 | | | | 99,97 |
| 5,79 | 7,55 | 91,72 | 0,72 | | | 99,99 |
| 6,75 | 0,83 | 92,48 | 6,66 | | | 99,97 |
| 7,72 | | 58,86 | 39,54 | 1,55 | | 99,95 |
| 8,79 | | 8,90 | 64,04 | 26,90 | 0,16 | 100,00 |
| 9,71 | | 0,30 | 19,79 | 75,82 | 4,08 | 99,99 |
| 10,74 | | | 1,52 | 62,44 | 36,03 | 99,99 |
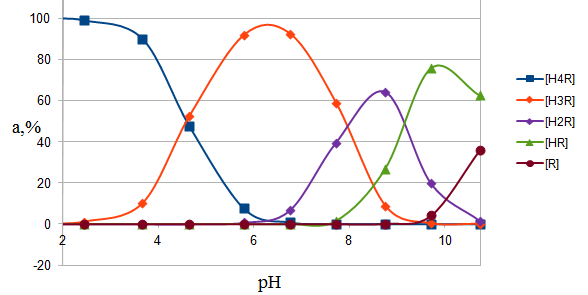
Рис. 3. Распределение форм ПАР в зависимости от рН
2.2. Исследование реакции комплексообразования железа с ПАР
Анализ кривых светопоглощения растворов комплексов железа с ПАР, снятых в широком интервале рН позволил сделать вывод о том, что в системе образуется одно комплексное соединение.
Максимум полосы поглощения данного комплекса находится при длине волны 540 нм.
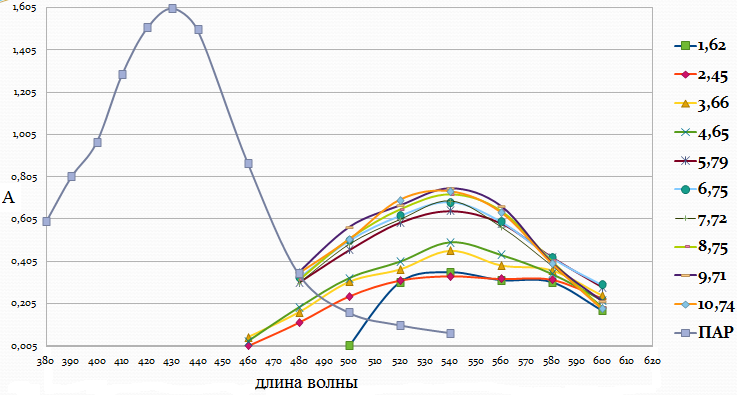
Рис. 4. Спектры поглощения комплекса Fe : ПАР в зависимости от рН раствора (CFe=1*10-5 моль/ дм3, СПАР = 5*10-5 моль/ дм3, l=10мм).
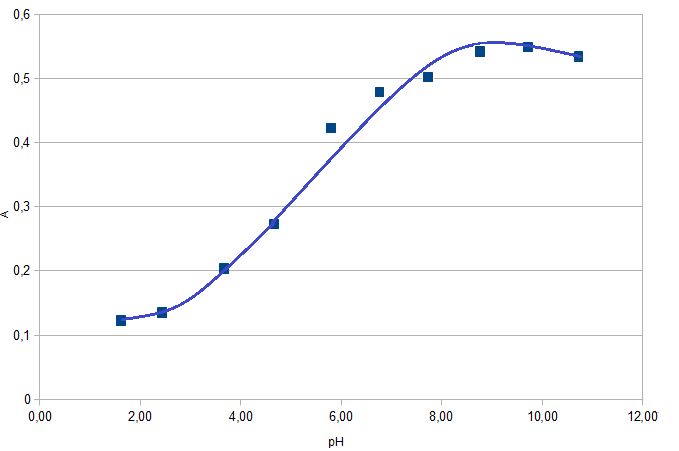
Рис. 5. Зависимость оптической плотности комплекса
Fe с ПАР от рН при 540 нм.
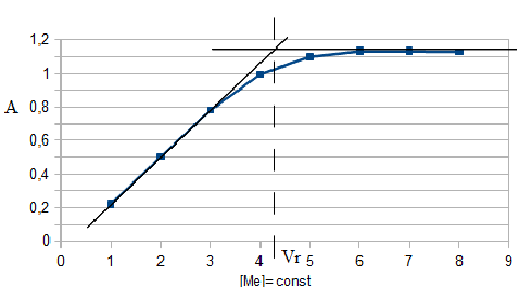
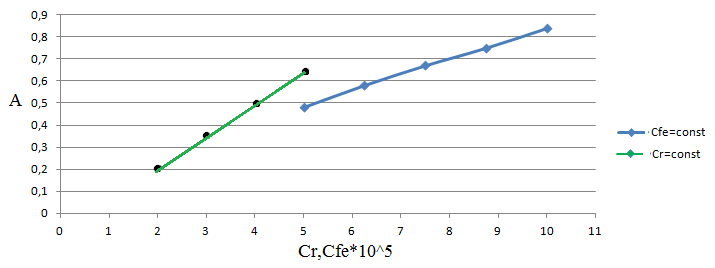
В условиях максимального светопоглощения был определен состав комплекса. Существует много способов определения состава комплексных соединений. Наиболее простым из них является метод изомолярных серий или метод Остромысленского-Жоба. Для определения состава комплекса этим методом были измерены оптические плотности с различным соотношением Fe : ПАР при постоянной концентрации железа и ПАР (рис. 6).
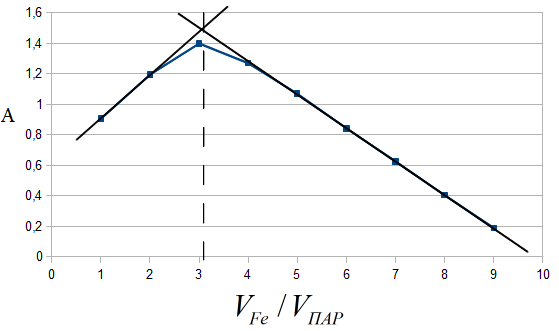
Рис. 6. Метод изомолярных серий
( CFe=СПАР = 1*10-4 моль/ дм3, l=10мм, λ=540 нм)
Как видно из рисунка, соотношение Fe : ПАР=1:2. Однако методом изомолярных серий можно определить только простейшую — эмпирическую формулу соединения. Более информативным является метод насыщения (рис.7). Из рисунка видно, что насыщение и по реагенту, и по металлу указывает на образование комплекса состава Ме:R= 1:2.
А
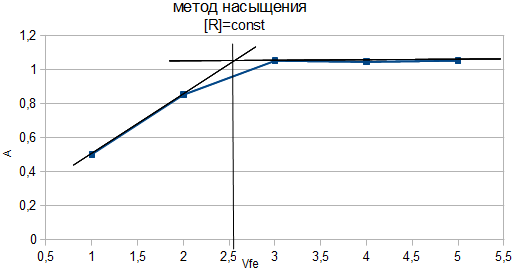
 )
)Б)
Рис. 7. Определение состава комплекса методом насыщения
СFe=CR=1·10-4-исходные, рН=9,0, λ=590нм, Vоб=10см3,
а) СR=const=5·10-5моль/ дм3 б) СFe=const=2·10-5моль/ дм3
Экспериментальные данные, полученные при
определении состава комплексов методом насыщения, позволили применить расчетные методы: метод прямой линии Асмуса, метод сдвига равновесия и метод отношения наклонов (Гарвея- Меннинга) [29,30]. Данные этих методов приведены на рис. 8-10.
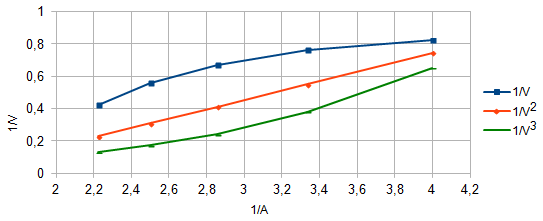
Рис. 8. Метод прямой линии Асмуса
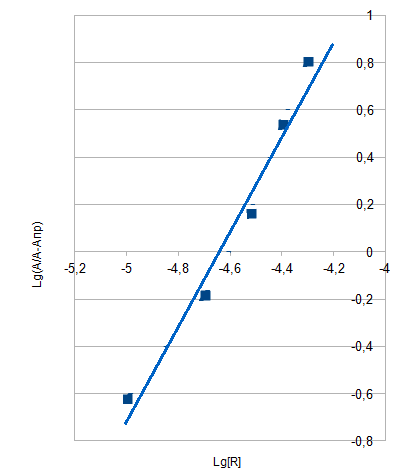
Р
 ис 9. Метод сдвига равновесия
ис 9. Метод сдвига равновесияРис.10. Метод отношения наклонов (Гарвея-Меннинга)
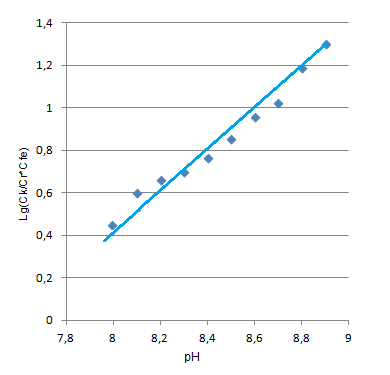
Из сопоставления кривых (рис.8) следует, что только n=2 удовлетворяет требованию прямолинейности функции Асмуса. Прямолинейная зависимость при n=2указывает на образование комплексного соединения состава 1:2.
В методе сдвига равновесия (рис. 9) тангенс угла наклона прямой к оси абсцисс имеет значение, близкое к 2, что соответствует образованию комплекса состава 1:2.
Метод Гарвея-Меннинга также соответствует соотношению компонентов в комплексе Fe-ПАР 1:2. Таким образом, различными методами показано, что соотношение компонентов в комплексе равно 1:2.
Для установления вида образующегося комплекса и определения его константы устойчивости изучали зависимость оптической плотности от рН раствора.
Общую схему комплексообразования ионов Fe с ПАР можно представить следующим образом:
F
Константа равновесия этой реакции равна
где СFe , CL - равновесные концентрации железа и ПАР,
Ск- концентрация комплекса,
СН+- концентрация ионов водорода.
Логарифмируя выражение (2):
получаем уравнение прямой в координатах
Графическое решение уравнения (4)дает возможность определить число протонов (n), участвующих в реакции комплексообразования.
Р
 авновесные концентрации металла и комплекса находили из зависимости оптической плотности от рН раствора (рис. 5) и рассчитывали по формулам:
авновесные концентрации металла и комплекса находили из зависимости оптической плотности от рН раствора (рис. 5) и рассчитывали по формулам:где Ах и А0- оптическая плотность при полном и неполном связывании металла в комплекс,
Сfe3+ и С0Fe3+- равновесная (при данном рН) и исходная концентрация Fe,
СПАР и С0ПАР- равновесная (при данном рН) и исходная концентрация ПАР.
Данные для определения числа протонов приведены в таблице 7. Графическая интерпретация представлена на рис. 11.
Таблица 7
Определение числа протонов
(С0Fe=2*10-4M, C0ПАР=5*10-4М, А0=0,565)
| рН | 8,0 | 8,1 | 8,2 | 8,3 | 8,4 | 8,5 | 8,6 | 8,7 | 8,8 | 8,9 |
| Ах | 0,530 | 0,532 | 0,536 | 0,539 | 0,542 | 0,546 | 0,549 | 0,552 | 0,556 | 0,558 |
| Ск*105 | 0,938 | 0,942 | 0,949 | 0,954 | 0,959 | 0,966 | 0,972 | 0,977 | 0,984 | 0,988 |
| СFe*105 | 0,066 | 0,054 | 0,048 | 0,036 | 0,031 | 0,027 | 0,020 | 0,018 | 0,014 | 0,009 |
| CПАР*105 | 4,066 | 4,054 | 4,048 | 4,038 | 4,031 | 4,027 | 4,020 | 4,018 | 4,014 | 4,009 |
| СFeCПАР*1010 | 0,270 | 0,220 | 0,200 | 0,104 | 0,120 | 0,110 | 0,080 | 0,070 | 0,060 | 0,040 |
| lg(Ск/СFeCПАР) | 0,540 | 0,640 | 0,690 | 0,830 | 0,900 | 0,960 | 1,090 | 1,140 | 1,240 | 1,440 |