ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 35
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ОГЛАВЛЕНИЕ.
ВВЕДЕНИЕ. 3
ОСНОВНАЯ ЧАСТЬ. 4
I. Квадратичные формы. 4
1.Определения. Примеры. 4
2. Приведение квадратичной формы к каноническому виду. 5
3.Положительно определённые квадратичные формы. 9
4. Квадратичные формы в евклидовом пространстве. 10
II. Квадрики. 13
1. Определения. Примеры. 13
2. Приведение уравнения квадрики к нормальному виду. 14
3. Центр квадрики. 16
4. Аффинная классификация квадрик. 17
5. Квадрики в Евклидовом пространстве. 19
ЗАКЛЮЧЕНИЕ. 22
ЛИТЕРАТУРА. 23
ВВЕДЕНИЕ.
Теория евклидовых пространств зиждется на положительно определенной квадратичном форме, с помощью которой они и задаются. Но в математических, так же как и в механических и физических джунглях, мы встречаемся со многими другими квадратичными формами. Как сказал Дьедонне, нет ни одной математической теории, в которой не участвовала бы какая-нибудь билинейная форма. Упомянем здесь хотя бы следующие примеры:
гильбертовы пространства и соболевские пространства в анализе; квадратичная или альтернированная форма, определяющая u-произведение на когомологиях средней размерности компактного многообразия; в теории чисел: разложение чисел в суммы квадратов; в дифференциальной геометрии: риманова геометрия или геометрия лоренцевых многообразий, используемых в теории отно сительности;
в механике: форма Лиувилля и вся симплектическая геометрия, а также теория торсоров.
В данной работе мы затронем несколько вопросов теории квадратичных форм и квадрик, имея в виду прежде всего геометрические приложения: определения и приведение к каноническому и нормальному виду квадратичных форм и квадрик, классификация квадрик в двумерном и трёхмерном аффинном и евклидовом пространствах и др.
ОСНОВНАЯ ЧАСТЬ.
I. Квадратичные формы.
1.Определения. Примеры.
Рассматриваем квадратичные формы только над полем действительных чисел R.
Определение. Квадратичной формой f(x1,…,xn)
над R от неизвестных x1, ..., xn называется однородный многочлен
степени 2, где
Таким образом, каждый член квадратичной формы содержит или квадрат одной из переменных, или произведение двух разных переменных.
Переменные
Пример 1.
Пример 2.
Матрица
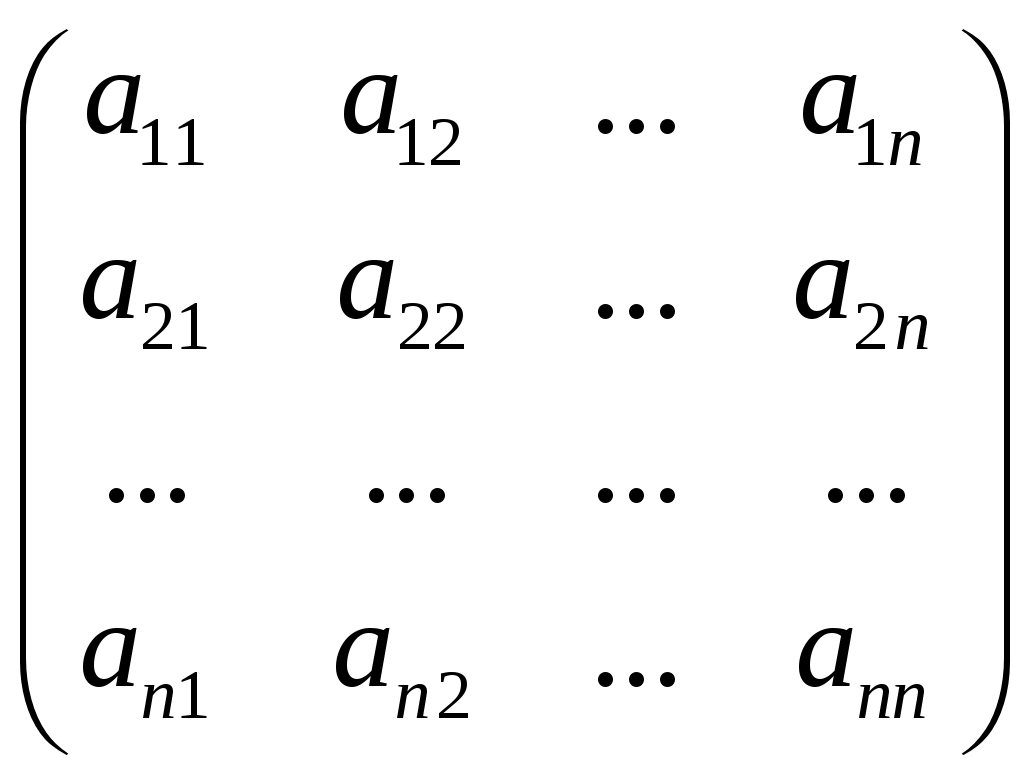
называется матрицей квадратичной формы (1). Так как
, то эта матрица симметрическая: её элементы симметричные относительно главной диагонали равны между собой.
Линейным преобразованием переменных называется такой переход от системы n переменных
или,
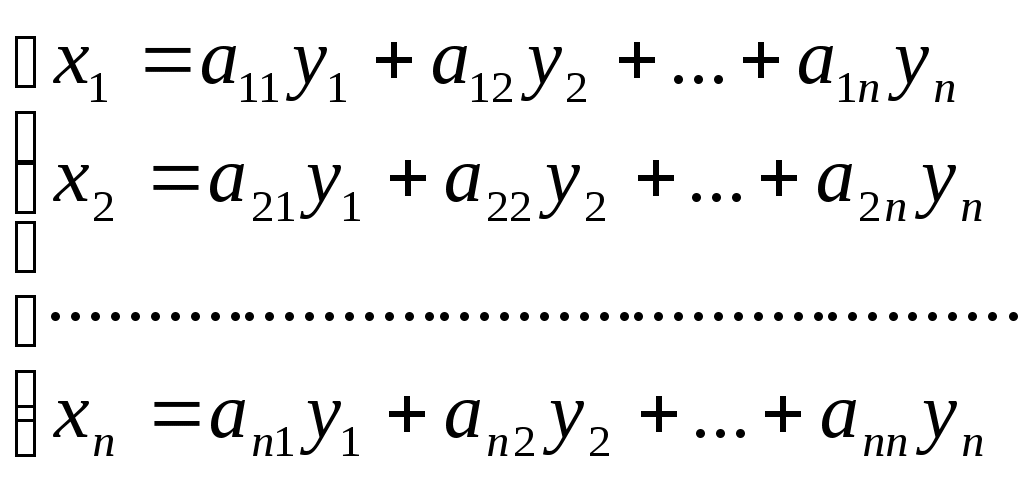 (2)
(2)где коэффициенты
Если переменные
В дальнейшем мы будем рассматривать квадратичные формы и линейные преобразования только с действительными коэффициентами. Будем считать, что и переменные принимают лишь действительные значения.
Если в квадратичной форме (1) переменные подвергнуть линейному преобразованию (2), то получится квадратичная форма от переменных
Любую квадратичную форму 2 можно привести к виду, содержащему только квадраты новых переменных
Такой вид квадратичной формы называется каноническим; матрица формы в этом случае является диагональной
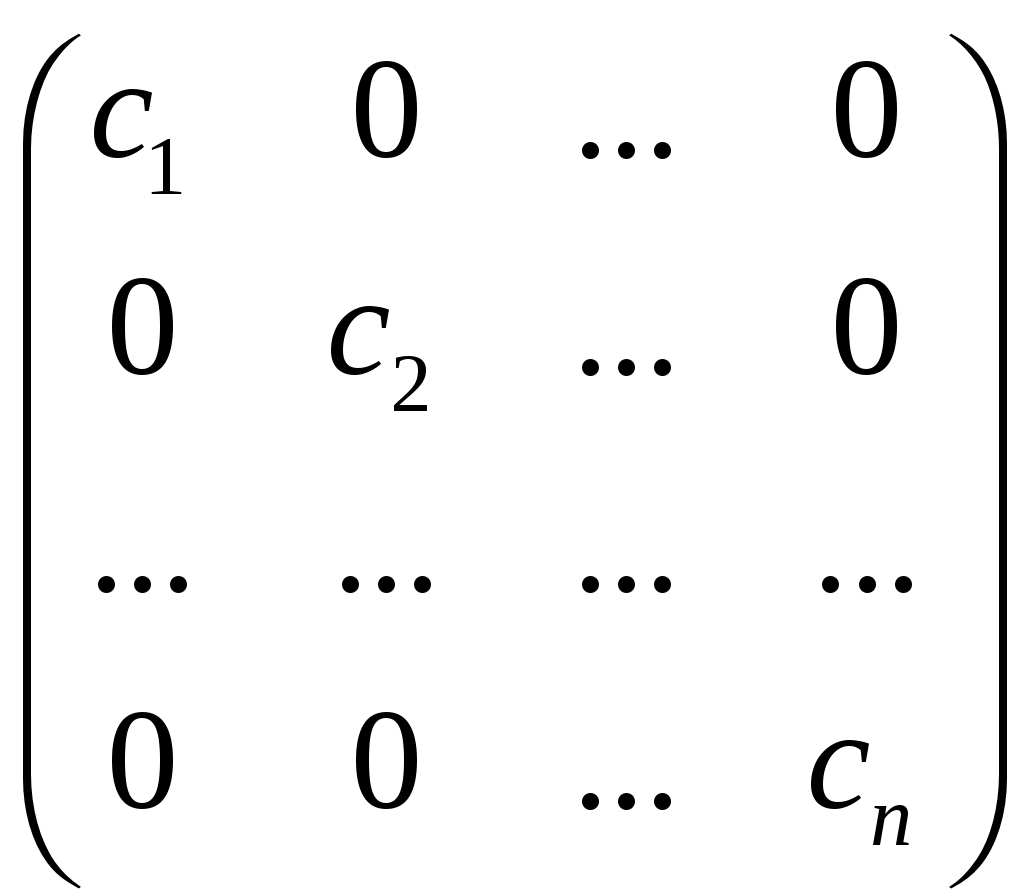
Если, в частности, коэффициенты
равны
Пример 3. Известно, что уравнение центральной кривой 2-го порядка
с помощью перехода к новой системе координат по формулам
можно привести к виду
Квадратичная форма
2. Приведение квадратичной формы к каноническому виду.
Лемма 1. Если квадратичная форма
не содержит квадратов переменных, то с помощью линейного преобразования ее можно привести в форму, содержащую квадрат хотя бы оной переменной.
Доказательство. По условию квадратичная форма содержит только члены с произведениями переменных. Пусть при каких-нибудь различных значениях
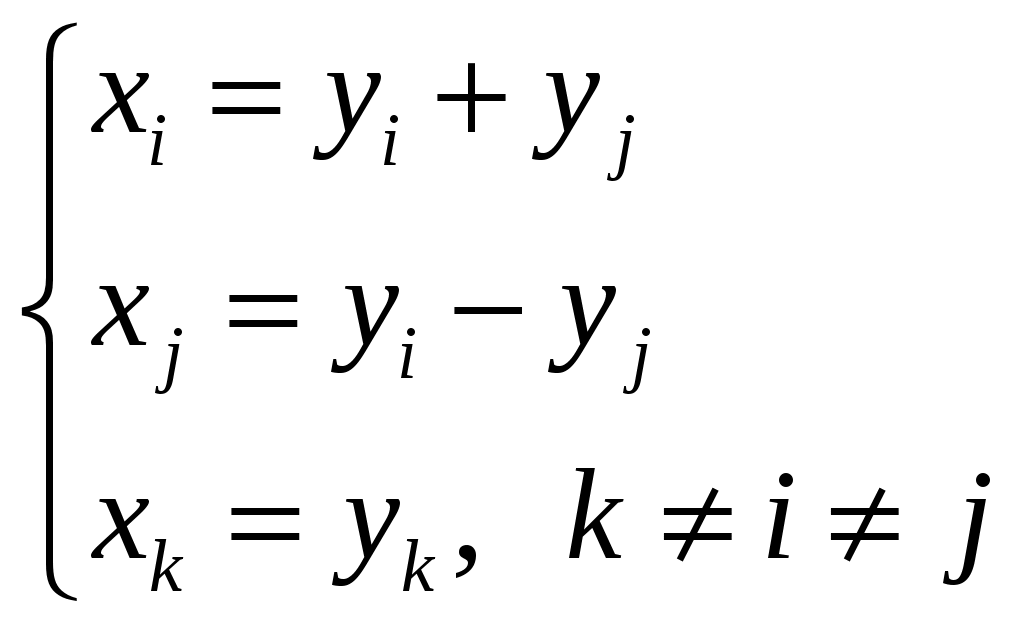
(его определитель не равен 0), то в квадратичной форме появятся даже два члена с квадратами переменных
Эти слагаемые не могут исчезнуть после приведения подобных членов, т.к. любое из остальных слагаемых содержит хотя бы одну переменную, отличную от yiиyj.
Лемма 2. Если квадратичная форма (3) содержит член с квадратом переменной, например член
где g – квадратичная форма, не содержащая переменной yi.
Доказательство. Выделим в квадратичной форме (3) сумму членов, содержащих переменную xi:
где через g1 обозначена сумма всех остальных членов (не содержащих переменную xi). Введем также обозначение
Квадрат многочлена равен сумме квадратов всех его членов, сложенной с удвоенными произведениями каждого члена на каждый из последующих. Следовательно, если в выражении для yi2 выделить сумму членов, содержащих переменную xi, то эта сумма будет содержать квадрат члена aiixi и удвоенное произведение этого члена aiixi на остальные члены многочлена
где g2 – сумма членов, не содержащих переменную xi.
Разделим обе части выражения (6) на aii и вычтем полученное равенство из выражения (5). После приведения подобных членов будем иметь
Выражение в правой части не содержит переменной xi и является квадратичной формой от переменных x1, x2,…,xi-1,xi+1,…,xn. Обозначим его через g, а коэффициент
Если произвести линейное преобразование
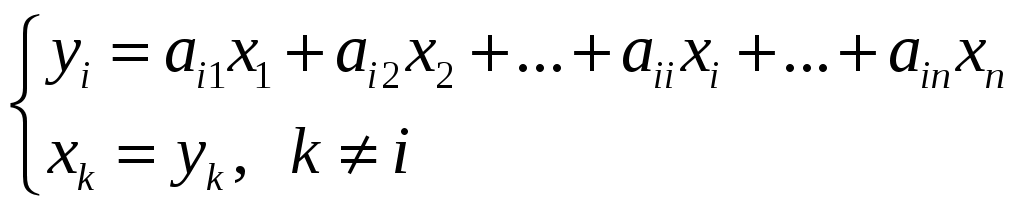 (определитель которого не равен 0), то g будет квадратичной формой от переменных
(определитель которого не равен 0), то g будет квадратичной формой от переменных Теорема. Всякая квадратичная форма может быть приведена к каноническому виду с помощью линейного преобразования переменных.

