ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 38
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
и  при
при 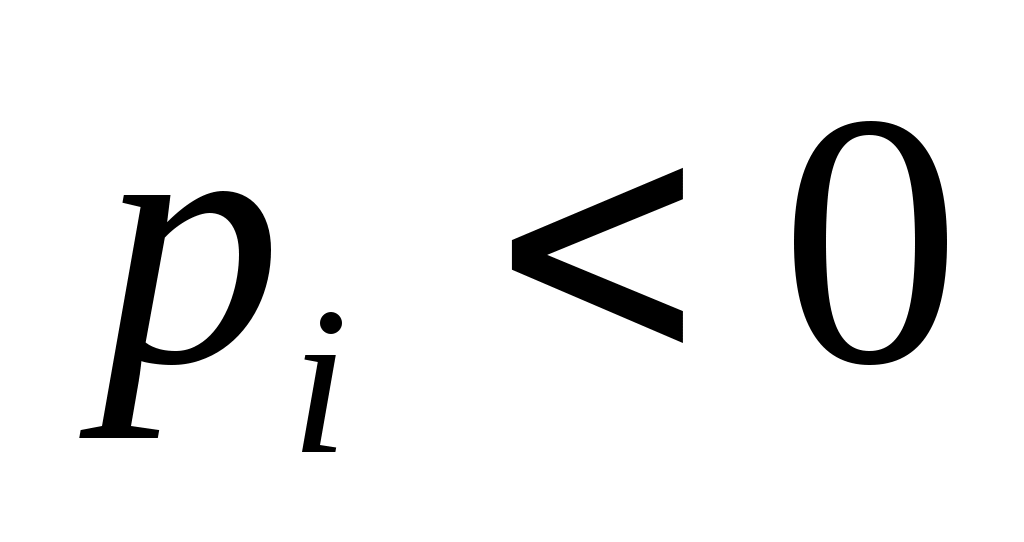 ;
;
3) пусть теперь m<n и хотя бы один из коэффициентов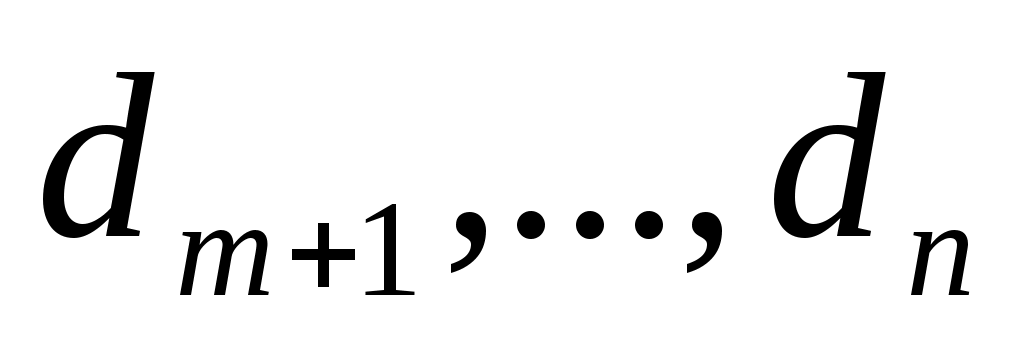 отличен от нуля, например,
отличен от нуля, например, 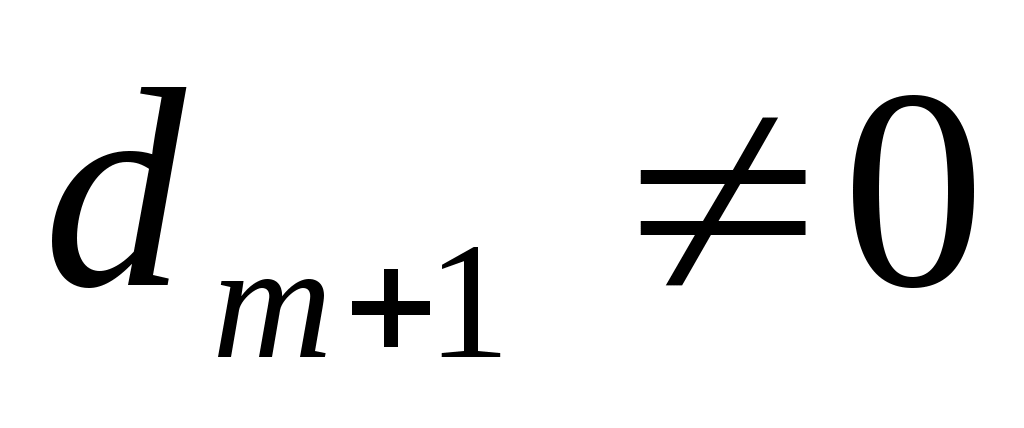 . Выполнив преобразование координат по формулам
. Выполнив преобразование координат по формулам
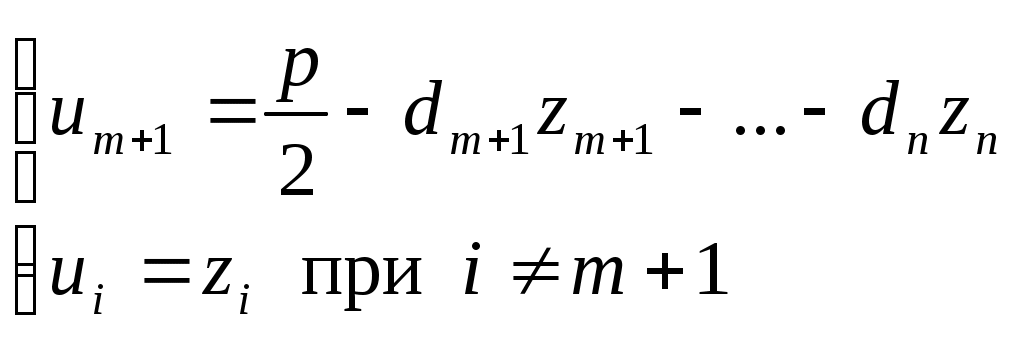
приведем уравнение (24) к виду
 .
.
После преобразования координат по формулам
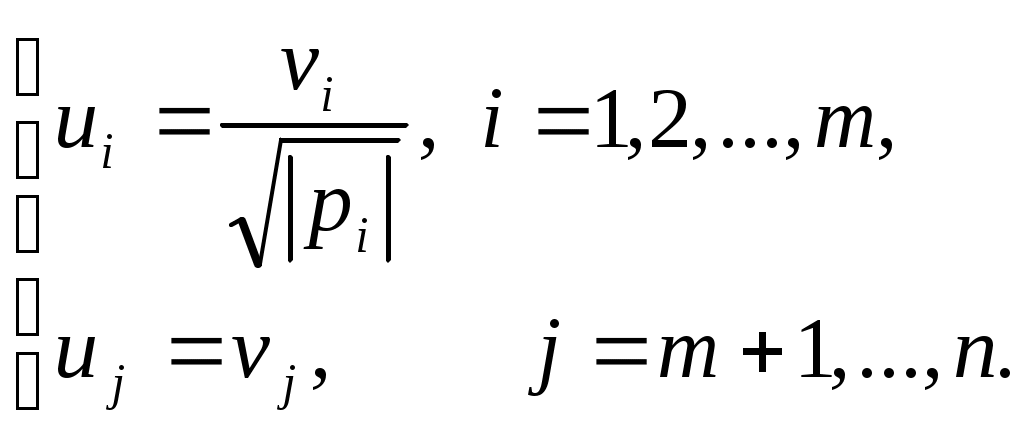
получим уравнение

где при
при  и
и  при
при 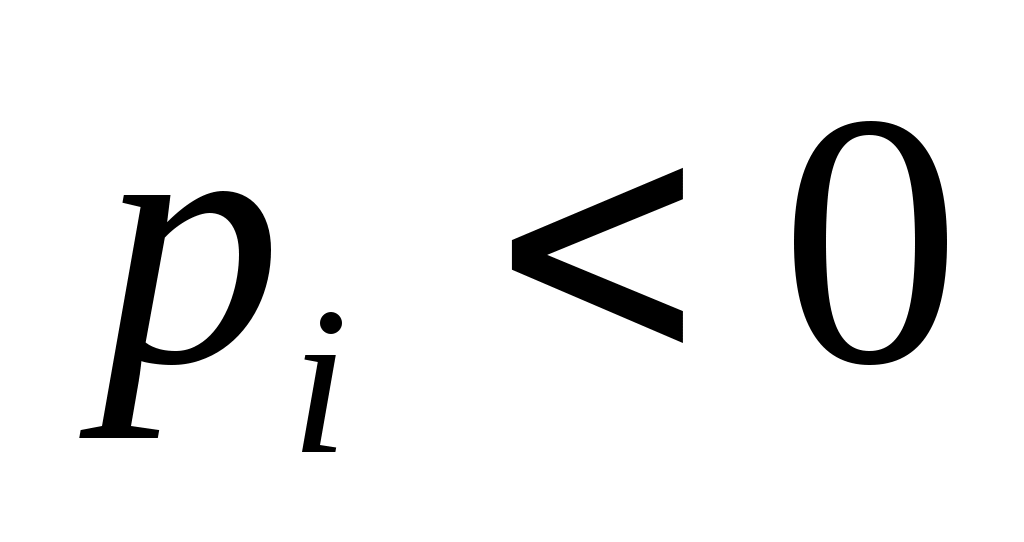 .
.
Теорема доказана полностью.
Уравнения (21), (22), (23) называются нормальными видами уравнения квадрики.
Определение. Точка S называется центром симметрии или просто центром квадрики, если точка, симметричная любой точке квадрики относительно S, также принадлежит квадрике.
Теорема. Если уравнение квадрики имеет вид (21) или (22), то точка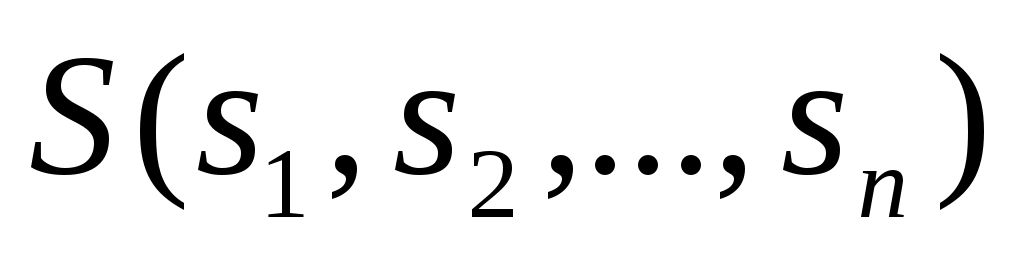 , для которой
, для которой 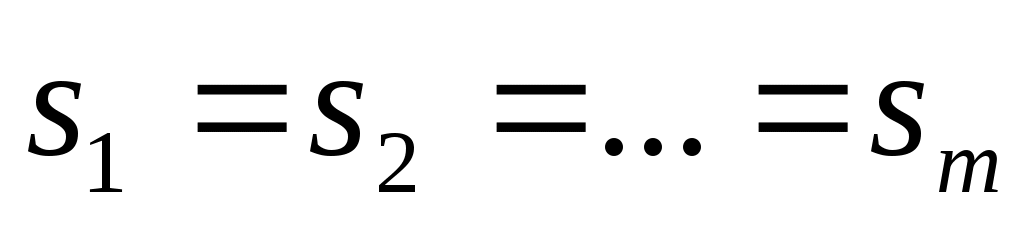 , является центром квадрики.
, является центром квадрики.
Доказательство. Если точки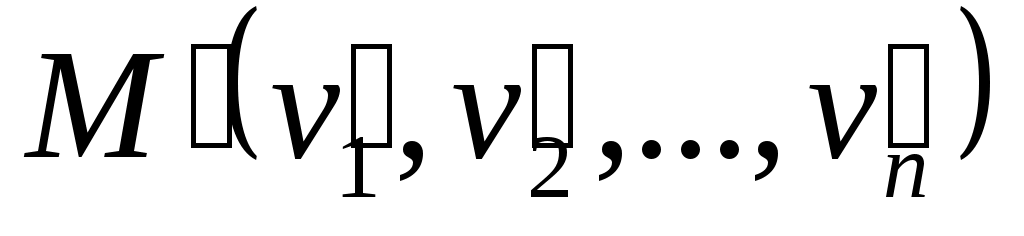 и
и 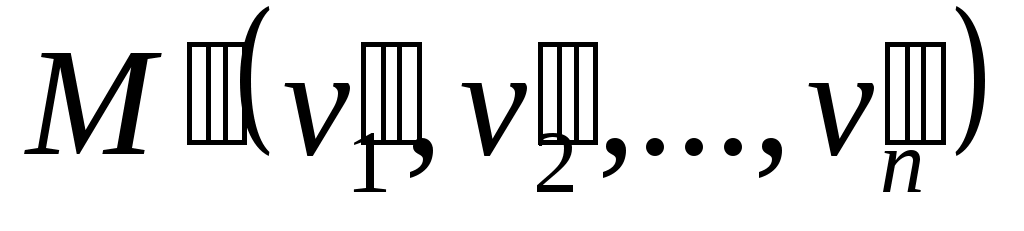 симметричны относительно точки S, то
симметричны относительно точки S, то
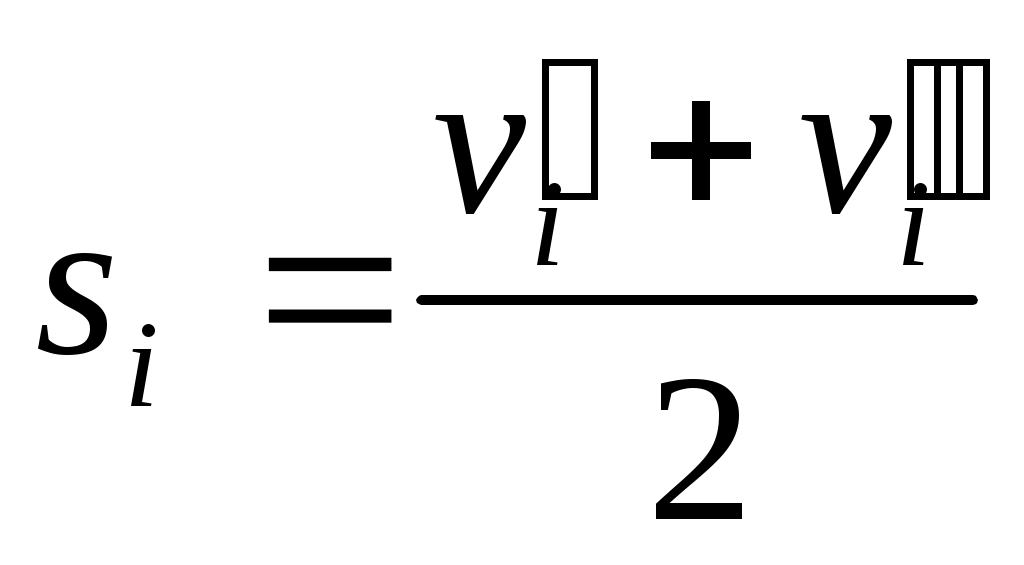 ,
,
откуда
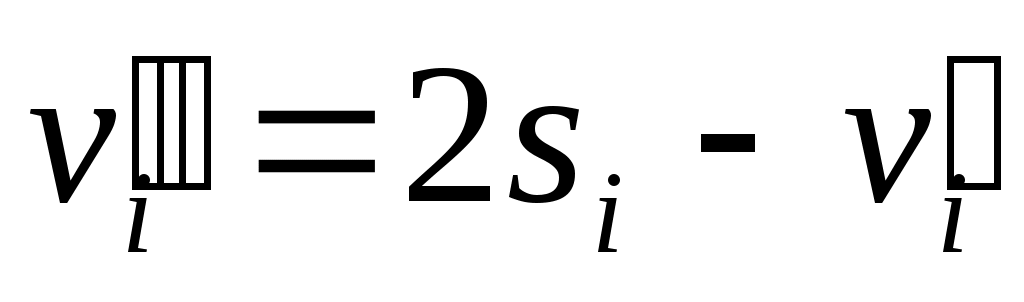
Т.к. s1= s2=…= sm=0, то

Уравнения (21) и (22) содержат координаты точки только во второй степени; следовательно, если координаты точки M' удовлетворяют какому-либо из этих уравнений, то этому же уравнению удовлетворяют координаты точки M''. Т.к. точка M'' симметрична точке M' относительно S, то S – центр квадрики.
Из теоремы следует, что все точки (nm)-мерной плоскости, имеющей уравнения
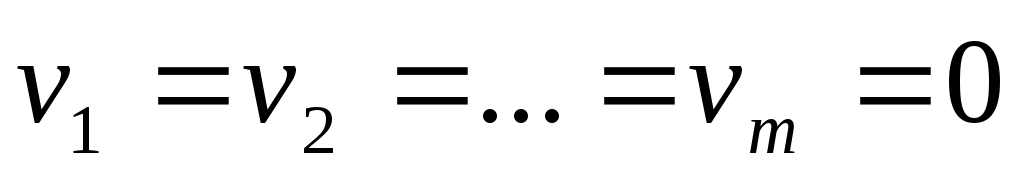 (25)
(25)
являются центрами квадрики (21) и (22); можно доказать, что других центров квадрика не имеет.
В частности, при m=n эта плоскость является нуль-мерной: уравнениям (15) удовлетворяют координаты единственной точки – начала координат. В этом случае квадрика имеет единственный центр.
Можно доказать, что квадрика (23) не имеет ни одного центра.
Т.к. уравнение квадрики всегда может быть приведено к виду (21), (22) или (23), то для любой квадрики имеет место один и только один из следующих трех случаев:
1) квадрика не имеет центра;
2) квадрика имеет единственный центр (тогда она называется центральной);
3) квадрика имеет бесконечное множество центров, являющееся некоторой плоскостью.
1. Эллипсоиды и гиперболоиды. При m=n уравнение (21) имеет вид
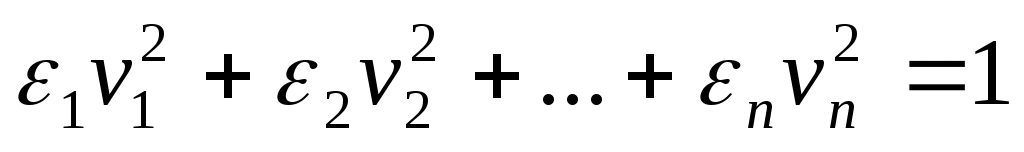 (26)
(26)
где равны +1 или 1.
равны +1 или 1.
В зависимости от знаков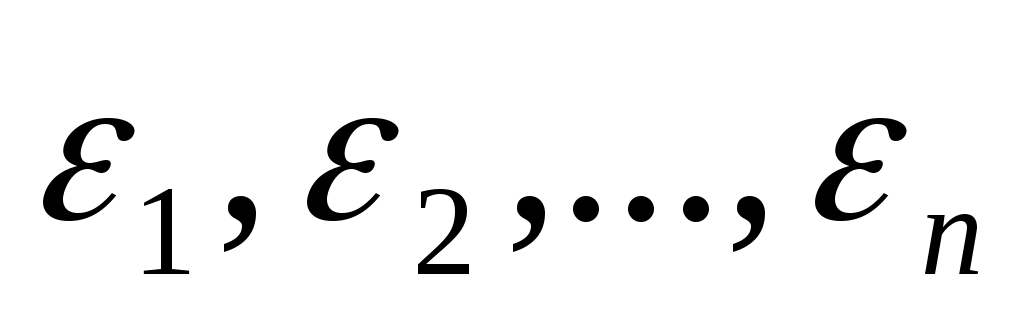 получаем квадрики различных видов:
получаем квадрики различных видов:
1) при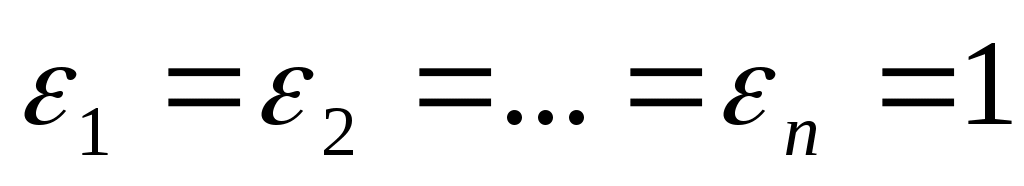 квадрика называется эллипсоидом и имеет уравнение
квадрика называется эллипсоидом и имеет уравнение
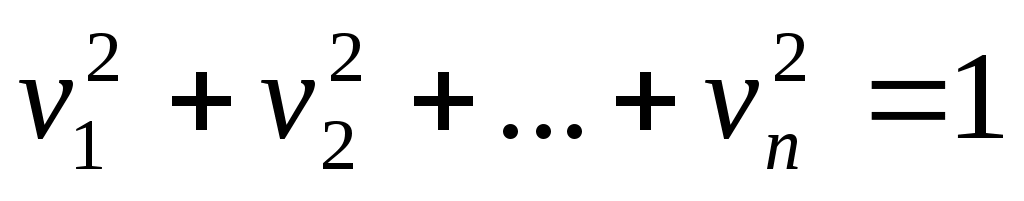
Внешне это уравнение напоминает уравнение сферы евклидова пространства в прямоугольной декартовой системе координат, однако следует помнить, что мы пользуемся единой системой координат, а понятие сферы в аффинной геометрии отсутствует.
2) при уравнение (26) принимает вид
уравнение (26) принимает вид
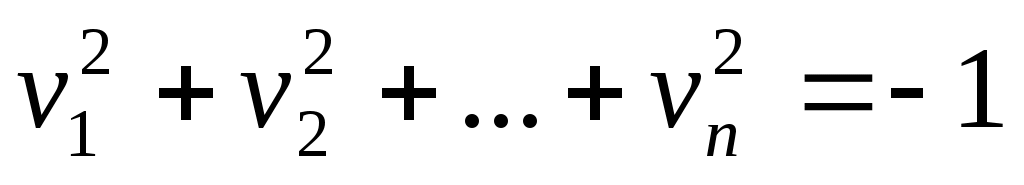
Т.к. мы рассматриваем действительное аффинное пространство
, то точек с координатами, удовлетворяющими этому уравнению, не существует. Однако по аналогии с предыдущим случаем это уравнение называют уравнением мнимого эллипсоида.
3) если не все одинаковы, то квадрика называется гиперболоидом.
не все одинаковы, то квадрика называется гиперболоидом.
Таким образом, эллипсоид и гиперболоид являются центральными квадриками.
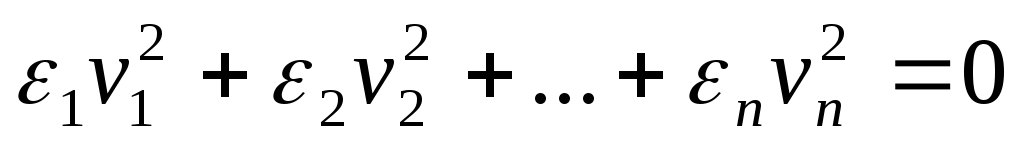 (27)
(27)
где равны +1 или 1.
равны +1 или 1.
1) Если знаки не все одинаковы, то квадрика называется конусом. Конус – центральная квадрика, центр конуса называется его вершиной. Центром конуса (27) является начало координат.
не все одинаковы, то квадрика называется конусом. Конус – центральная квадрика, центр конуса называется его вершиной. Центром конуса (27) является начало координат.
Если координаты точки А(а1, а2,…,аn), отличной от вершины конуса, удовлетворяют уравнению (27), то этому уравнению удовлетворяют и координаты любой точки вида (tа1, tа2,…,tаn). Множество всех таких точек является прямой, проходящей через А и вершину конуса – начало координат. Эта прямая целиком принадлежит конусу и называется его прямолинейной образующей.
2) Если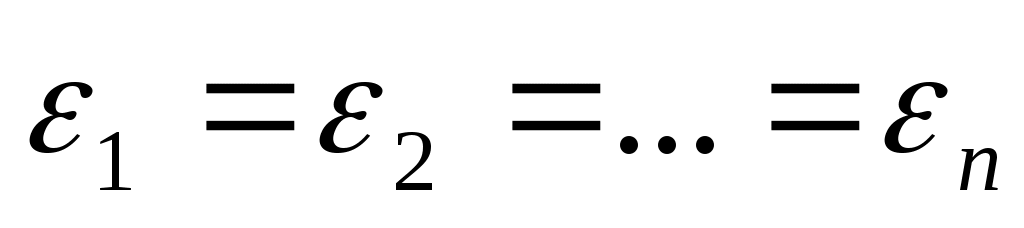 , то квадрика (27) состоит из единственной точки (начала координат) и называется мнимым конусом с вершиной в этой точке.
, то квадрика (27) состоит из единственной точки (начала координат) и называется мнимым конусом с вершиной в этой точке.
3. Параболоиды. При m=n1 уравнение (23) принимает вид
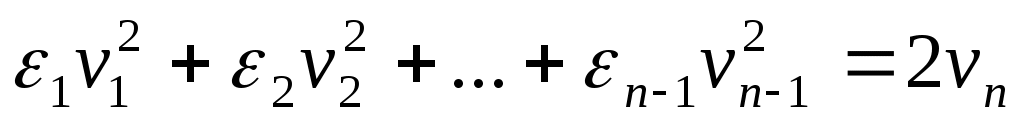 (28)
(28)
где равны +1 или 1.
равны +1 или 1.
Квадрика в этом случае называется параболоидом. Параболоид не имеет центра.
4. Цилиндрические квадрики. Если в уравнениях (21) и (22) m<n, а в уравнении (23) m<n1, то, полагая в (21) и (22) m=r, а в (23) m=r1, получим соответственно
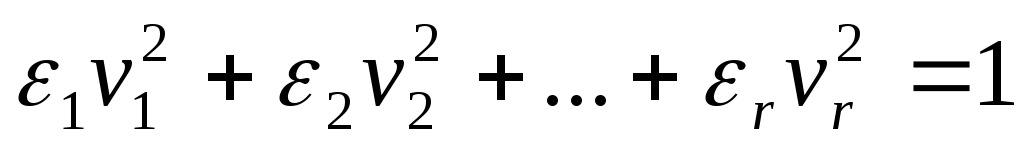 , (29)
, (29)
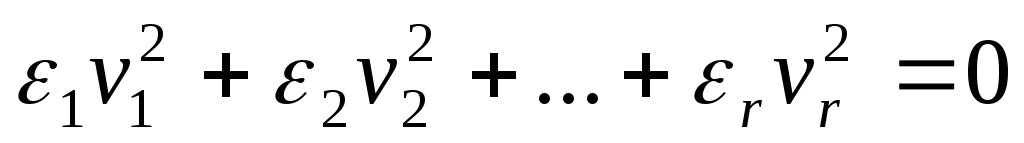 , (30)
, (30)
 , (31)
, (31)
где r<n и
равны +1 или 1.
Квадрика, для которой (29), (30) или (31) является нормальным уравнением, называется цилиндрической.
Можно показать, что цилиндрическая квадрика состоит из параллельных друг другу (nr)-мерных плоскостей (образующих), пересекающих некоторую квадрику (направляющую), лежащую в r-мерной плоскости. Квадрики (29) и (30) имеют в общем случае бесконечное множество центров, являющееся (nr)-мерной плоскостью. Квадрика (31) центров не имеет.
Аффинная классификация квадрик в пространстве А2. Уравнение любой квадрики может быть приведено к одному из следующих нормальных видов:
а) неконические центральные кривые:
1)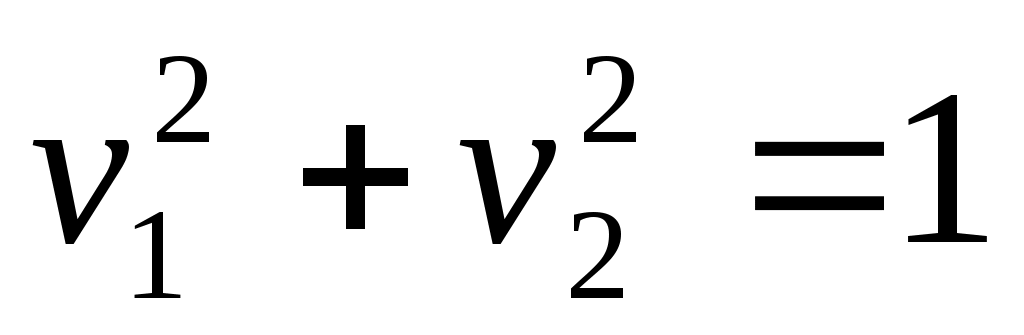 эллипс;
эллипс;
2)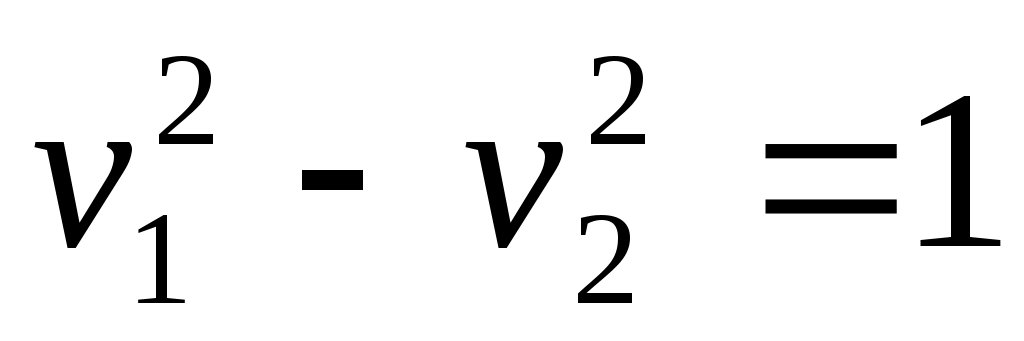 гипербола;
гипербола;
3)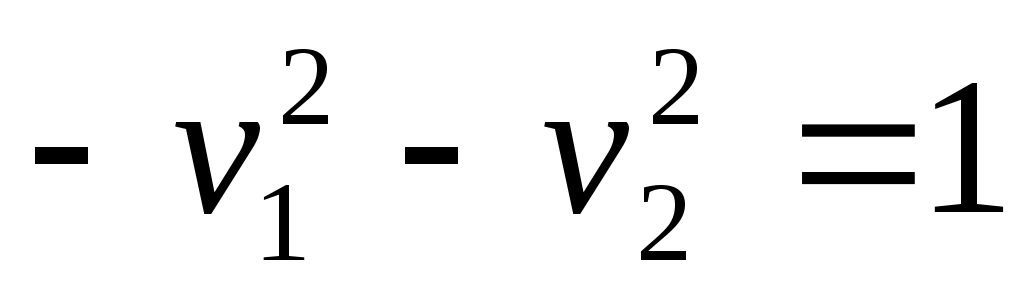 мнимый эллипс;
мнимый эллипс;
б) конические центральные кривые:
4)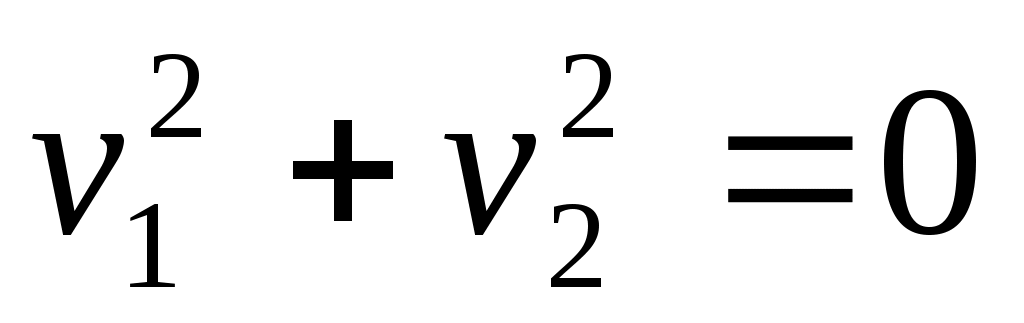 пара пересекающихся мнимых прямых;
пара пересекающихся мнимых прямых;
5)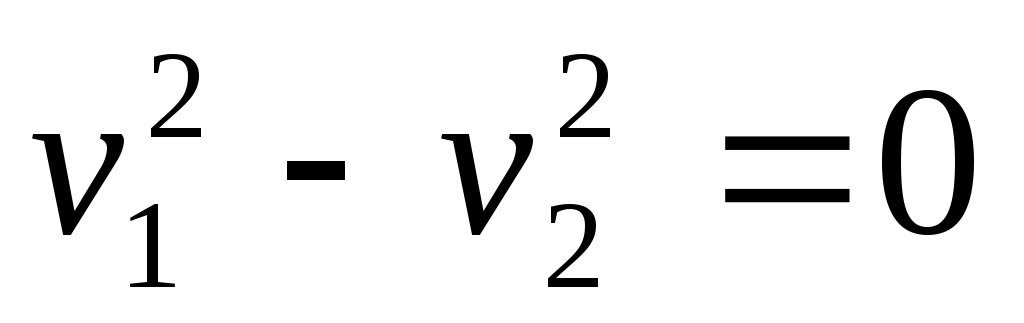 пара пересекающихся действительных прямых;
пара пересекающихся действительных прямых;
в) нецентральные нецилиндрические кривые:
6)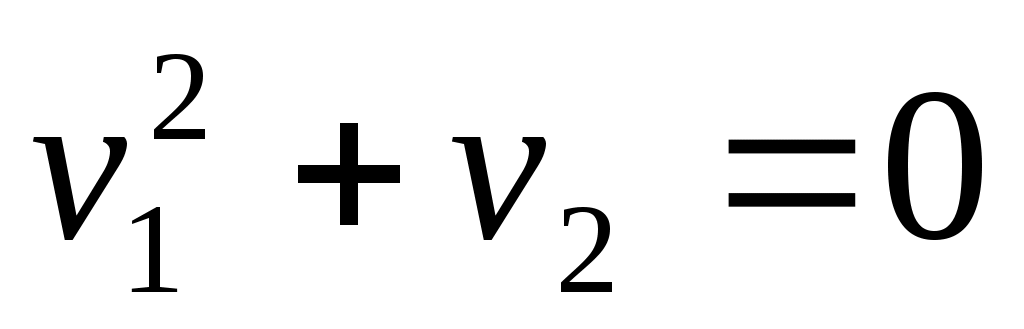 парабола;
парабола;
г) цилиндрические кривые, имеющие центры:
7)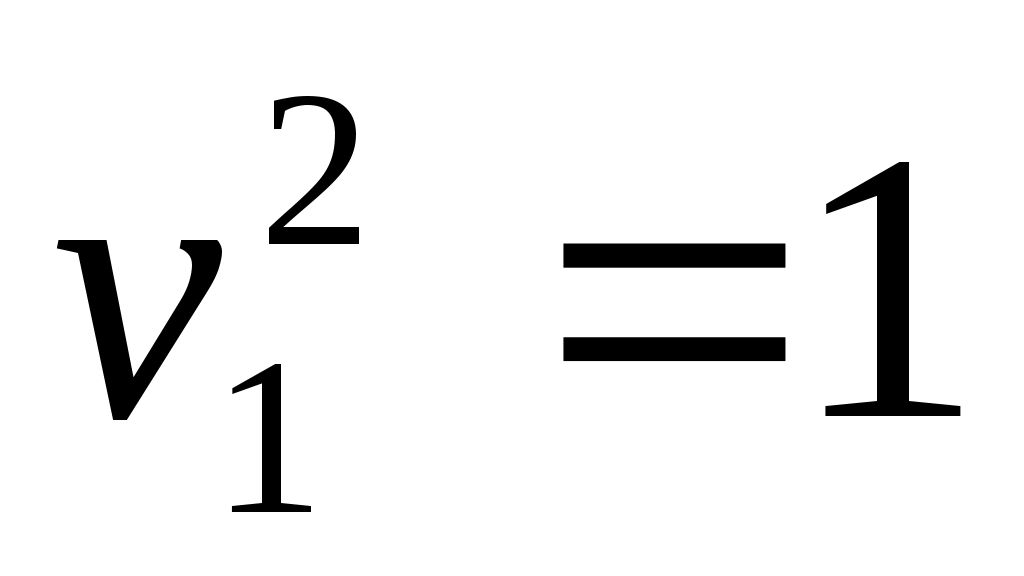 пара параллельных прямых;
пара параллельных прямых;
8)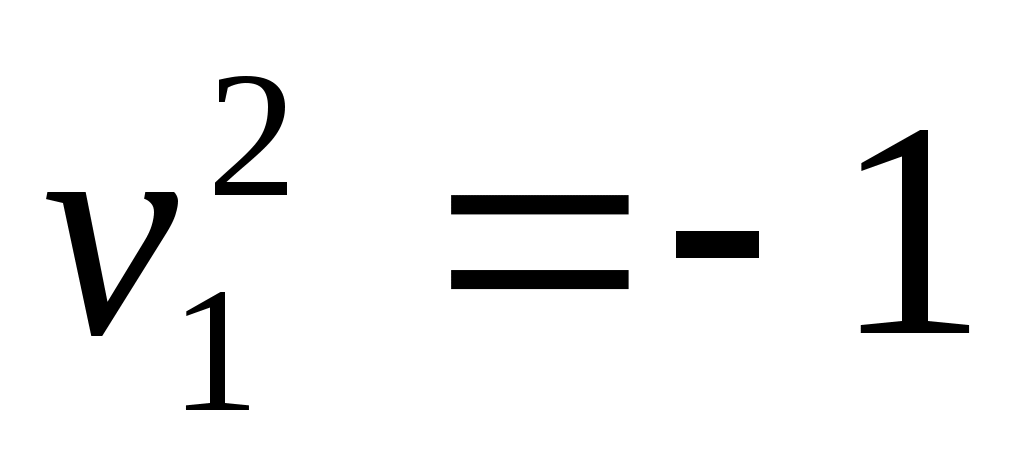 пара мнимых параллельных прямых;
пара мнимых параллельных прямых;
9)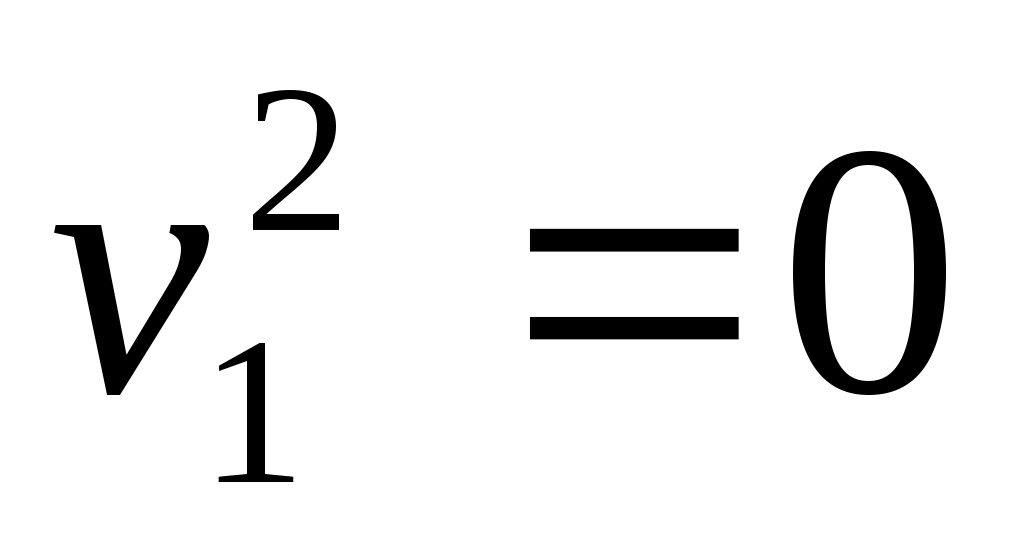 пара слившихся прямых.
пара слившихся прямых.
Любые две квадрики, принадлежащие к одному и тому же классу, аффинно эквивалентны. Это связано с тем, что формулы перехода от одной аффинной системы координат к другой и формулы аффинных преобразований с алгебраической точки зрения имеют один и тот же вид.
Заметим, что квадрики с различными нормальными уравнениями могут оказаться одинаковыми точечными множествами. Так, например, мнимый эллипс и пара мнимых параллельных прямых – пустое точечное множество. Поэтому квадрики, принадлежащие различным классам, иногда могут оказаться аффинно эквивалентными; с геометрической точки зрения эти классы тогда не различаются между собой.
Упрощение уравнения квадрики производится вначале по тому же плану, что и в п. II.2, с той лишь разницей, что квадратичная форма, содержащаяся в левой части уравнения (20), приводится к каноническому виду с помощью ортогонального преобразования (а не произвольного линейного, как раньше). С геометрической точки зрения это означает переход к новой прямоугольной декартовой системе координат, получаемой из исходной прямоугольной декартовой системы координат с помощью вращения вокруг начала координат. Подвергая затем полученную систему координат параллельному переносу, приведем уравнение квадрики к
 , (32)
, (32)
где mn и коэффициенты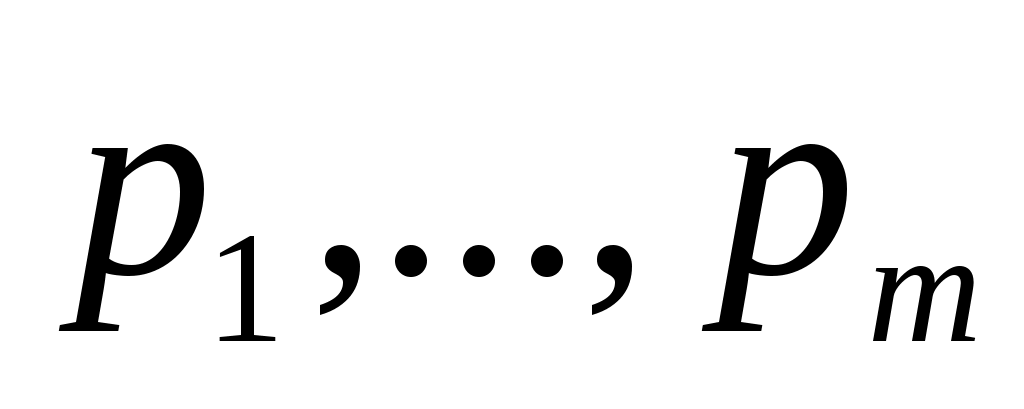 не равны нулю.
не равны нулю.
При дальнейшем упрощении уравнения квадрики обычно уже не удается добиться того, чтобы все коэффициенты при квадратах координат были равны +1 или 1. Это связано с тем, что при помощи ортогонального преобразования квадратичная форма не всегда приводится к нормальному виду. Поэтому в пространстве Еn уравнение квадрики в общем случае уже не удается привести к такому же простому виду, как в пространстве Аn.
Так как конгруэнтные фигуры являются также и аффинно эквивалентными, то аффинная классификация квадрик, установленная в п. II.4, остается в силе и для пространства Еn. Однако не всякие аффинно эквивалентные фигуры конгруэнтны; поэтому каждый из классов аффинной классификации может быть разбит на бесконечное множество классов так, что любые две квадрики из одного класса конгруэнтны, а любые две квадрики из разных классов не конгруэнтны. В связи с этим появляется возможность выделения новых видов квадрик, не рассматривавшихся в Аn.
6. Классификация квадрик в трёхмерном евклидовом пространстве.
Классификация квадрик в пространстве Е2 совпадает с приведённой ранее классификацией в пространстве А2
3) пусть теперь m<n и хотя бы один из коэффициентов
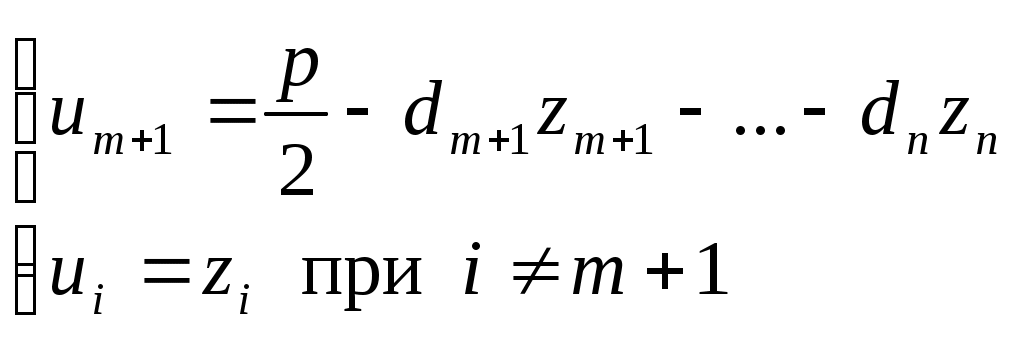
приведем уравнение (24) к виду
После преобразования координат по формулам
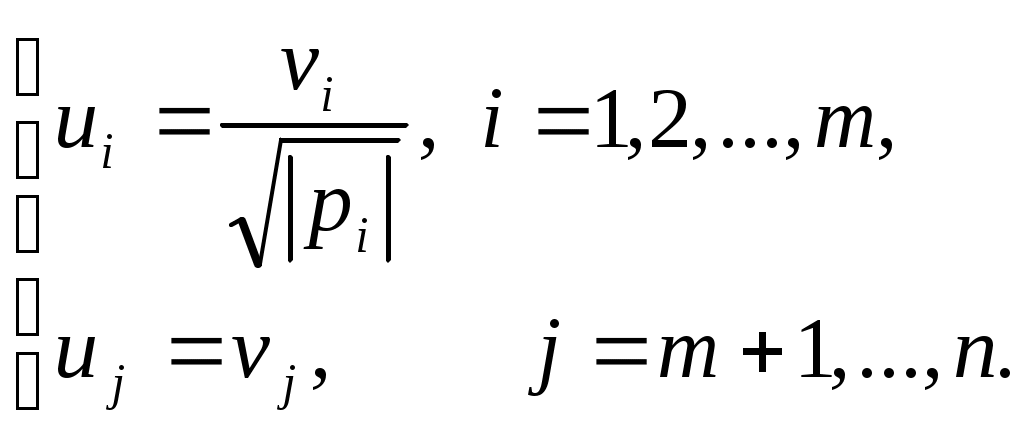
получим уравнение
где
Теорема доказана полностью.
Уравнения (21), (22), (23) называются нормальными видами уравнения квадрики.
3. Центр квадрики.
Определение. Точка S называется центром симметрии или просто центром квадрики, если точка, симметричная любой точке квадрики относительно S, также принадлежит квадрике.
Теорема. Если уравнение квадрики имеет вид (21) или (22), то точка
Доказательство. Если точки
откуда
Т.к. s1= s2=…= sm=0, то
Уравнения (21) и (22) содержат координаты точки только во второй степени; следовательно, если координаты точки M' удовлетворяют какому-либо из этих уравнений, то этому же уравнению удовлетворяют координаты точки M''. Т.к. точка M'' симметрична точке M' относительно S, то S – центр квадрики.
Из теоремы следует, что все точки (nm)-мерной плоскости, имеющей уравнения
являются центрами квадрики (21) и (22); можно доказать, что других центров квадрика не имеет.
В частности, при m=n эта плоскость является нуль-мерной: уравнениям (15) удовлетворяют координаты единственной точки – начала координат. В этом случае квадрика имеет единственный центр.
Можно доказать, что квадрика (23) не имеет ни одного центра.
Т.к. уравнение квадрики всегда может быть приведено к виду (21), (22) или (23), то для любой квадрики имеет место один и только один из следующих трех случаев:
1) квадрика не имеет центра;
2) квадрика имеет единственный центр (тогда она называется центральной);
3) квадрика имеет бесконечное множество центров, являющееся некоторой плоскостью.
4. Аффинная классификация квадрик.
1. Эллипсоиды и гиперболоиды. При m=n уравнение (21) имеет вид
где
В зависимости от знаков
1) при
Внешне это уравнение напоминает уравнение сферы евклидова пространства в прямоугольной декартовой системе координат, однако следует помнить, что мы пользуемся единой системой координат, а понятие сферы в аффинной геометрии отсутствует.
2) при
Т.к. мы рассматриваем действительное аффинное пространство
, то точек с координатами, удовлетворяющими этому уравнению, не существует. Однако по аналогии с предыдущим случаем это уравнение называют уравнением мнимого эллипсоида.
3) если
Таким образом, эллипсоид и гиперболоид являются центральными квадриками.
-
Конусы. При m=n уравнение (22) имеет вид
где
1) Если знаки
Если координаты точки А(а1, а2,…,аn), отличной от вершины конуса, удовлетворяют уравнению (27), то этому уравнению удовлетворяют и координаты любой точки вида (tа1, tа2,…,tаn). Множество всех таких точек является прямой, проходящей через А и вершину конуса – начало координат. Эта прямая целиком принадлежит конусу и называется его прямолинейной образующей.
2) Если
3. Параболоиды. При m=n1 уравнение (23) принимает вид
где
Квадрика в этом случае называется параболоидом. Параболоид не имеет центра.
4. Цилиндрические квадрики. Если в уравнениях (21) и (22) m<n, а в уравнении (23) m<n1, то, полагая в (21) и (22) m=r, а в (23) m=r1, получим соответственно
где r<n и
равны +1 или 1.
Квадрика, для которой (29), (30) или (31) является нормальным уравнением, называется цилиндрической.
Можно показать, что цилиндрическая квадрика состоит из параллельных друг другу (nr)-мерных плоскостей (образующих), пересекающих некоторую квадрику (направляющую), лежащую в r-мерной плоскости. Квадрики (29) и (30) имеют в общем случае бесконечное множество центров, являющееся (nr)-мерной плоскостью. Квадрика (31) центров не имеет.
Аффинная классификация квадрик в пространстве А2. Уравнение любой квадрики может быть приведено к одному из следующих нормальных видов:
а) неконические центральные кривые:
1)
2)
3)
б) конические центральные кривые:
4)
5)
в) нецентральные нецилиндрические кривые:
6)
г) цилиндрические кривые, имеющие центры:
7)
8)
9)
Любые две квадрики, принадлежащие к одному и тому же классу, аффинно эквивалентны. Это связано с тем, что формулы перехода от одной аффинной системы координат к другой и формулы аффинных преобразований с алгебраической точки зрения имеют один и тот же вид.
Заметим, что квадрики с различными нормальными уравнениями могут оказаться одинаковыми точечными множествами. Так, например, мнимый эллипс и пара мнимых параллельных прямых – пустое точечное множество. Поэтому квадрики, принадлежащие различным классам, иногда могут оказаться аффинно эквивалентными; с геометрической точки зрения эти классы тогда не различаются между собой.
5. Квадрики в Евклидовом пространстве.
Упрощение уравнения квадрики производится вначале по тому же плану, что и в п. II.2, с той лишь разницей, что квадратичная форма, содержащаяся в левой части уравнения (20), приводится к каноническому виду с помощью ортогонального преобразования (а не произвольного линейного, как раньше). С геометрической точки зрения это означает переход к новой прямоугольной декартовой системе координат, получаемой из исходной прямоугольной декартовой системы координат с помощью вращения вокруг начала координат. Подвергая затем полученную систему координат параллельному переносу, приведем уравнение квадрики к
где mn и коэффициенты
При дальнейшем упрощении уравнения квадрики обычно уже не удается добиться того, чтобы все коэффициенты при квадратах координат были равны +1 или 1. Это связано с тем, что при помощи ортогонального преобразования квадратичная форма не всегда приводится к нормальному виду. Поэтому в пространстве Еn уравнение квадрики в общем случае уже не удается привести к такому же простому виду, как в пространстве Аn.
Так как конгруэнтные фигуры являются также и аффинно эквивалентными, то аффинная классификация квадрик, установленная в п. II.4, остается в силе и для пространства Еn. Однако не всякие аффинно эквивалентные фигуры конгруэнтны; поэтому каждый из классов аффинной классификации может быть разбит на бесконечное множество классов так, что любые две квадрики из одного класса конгруэнтны, а любые две квадрики из разных классов не конгруэнтны. В связи с этим появляется возможность выделения новых видов квадрик, не рассматривавшихся в Аn.
6. Классификация квадрик в трёхмерном евклидовом пространстве.
Классификация квадрик в пространстве Е2 совпадает с приведённой ранее классификацией в пространстве А2

