ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 39
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Чтобы дать полную классификацию квадрик при п = 3, рассмотрим все частные случаи, которые могут представиться при упрощении уравнения (32).
Случай 1.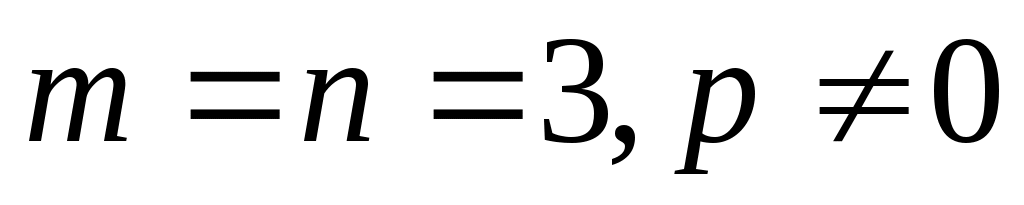 . Уравнение (32) принимает вид
. Уравнение (32) принимает вид
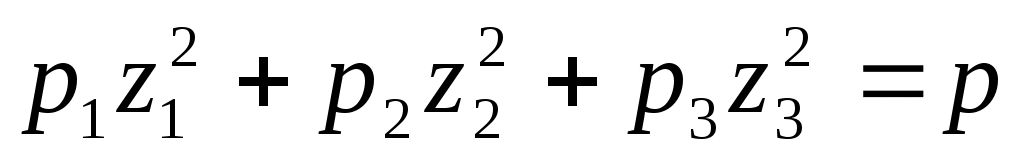 или
или 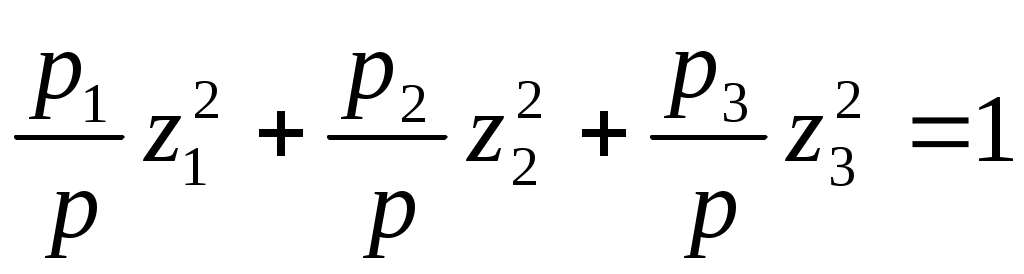 .
.
В зависимости от знаков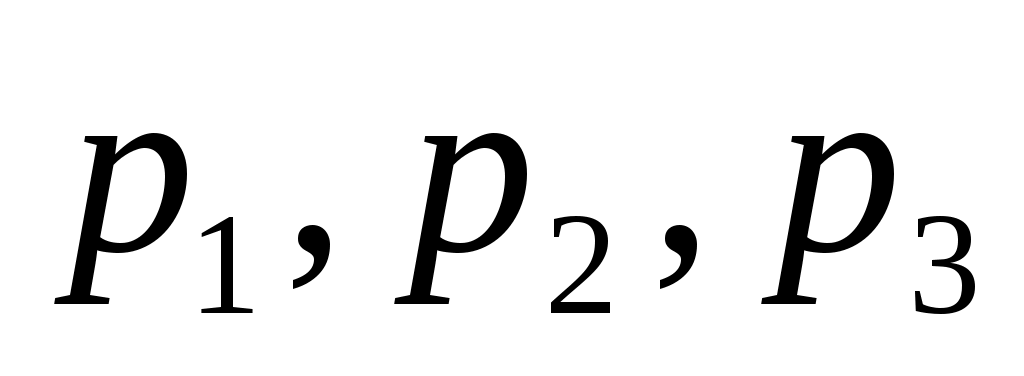 и p это уравнение можно записать в различных видах:
и p это уравнение можно записать в различных видах:
1)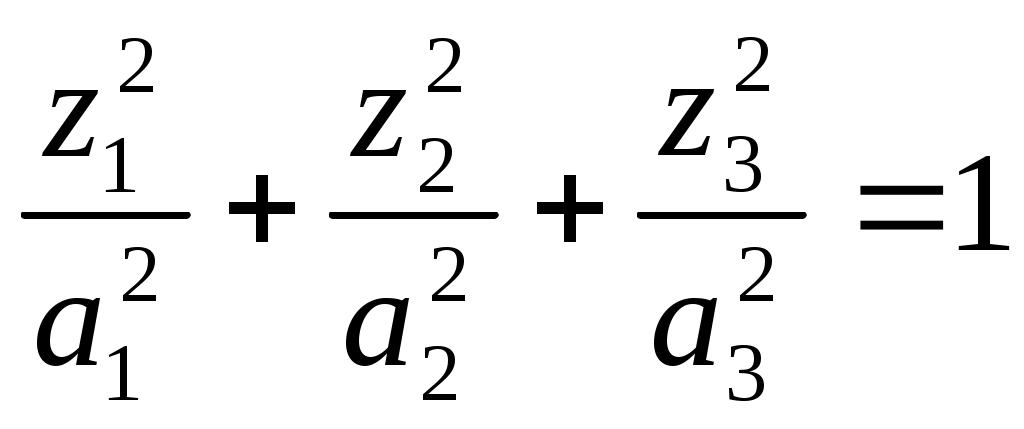 эллипсоид;
эллипсоид;
2)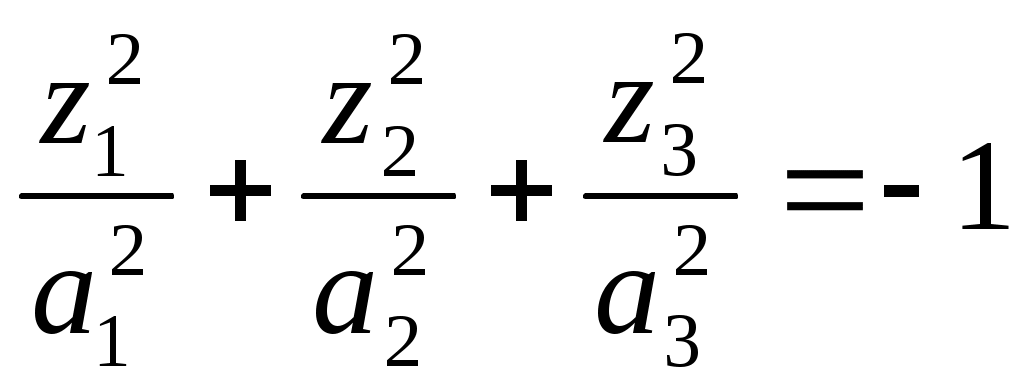 мнимый эллипсоид;
мнимый эллипсоид;
3)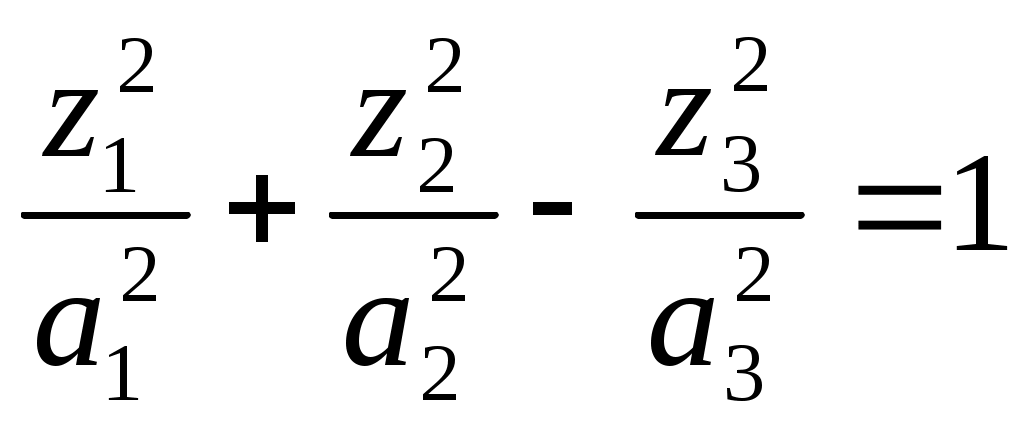 однополостный гиперболоид;
однополостный гиперболоид;
4)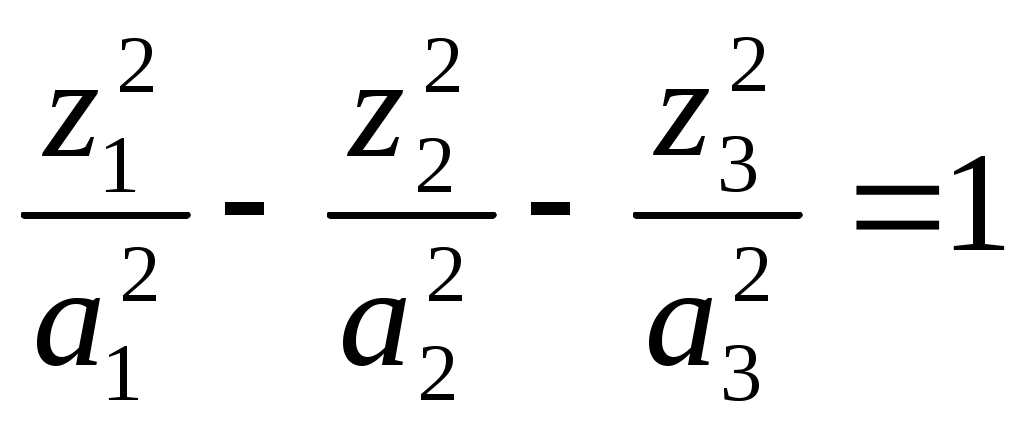 двуполостный гиперболоид.
двуполостный гиперболоид.
Все эллипсоиды аффинно эквивалентны и, следовательно, с точки зрения аффинной геометрии не отличаются друг от друга по своим свойствам. Однако не всякие два эллипсоида конгруэнтны и даже подобны; в связи с этим в евклидовой геометрии появляется возможность классификации эллипсоидов.
Если а1, а2, а3 различны, то эллипсоид называется трехосным. Если равны какие-нибудь два из чисел
а1, а2, а3, то эллипсоид называется эллипсоидом вращения. Если а1 = а2 = а3, то эллипсоид является сферой. Эта классификация инвариантна относительно движений; например, любое движение может отобразить сферу также только на сферу. Поэтому указанные виды эллипсоидов являются объектами, изучаемыми в евклидовой геометрии.
Аналогичные замечания можно сделать и относительно других видов квадрик(например, можно выделить гиперболоиды вращения, конус вращения и т. п.).
Случай 2.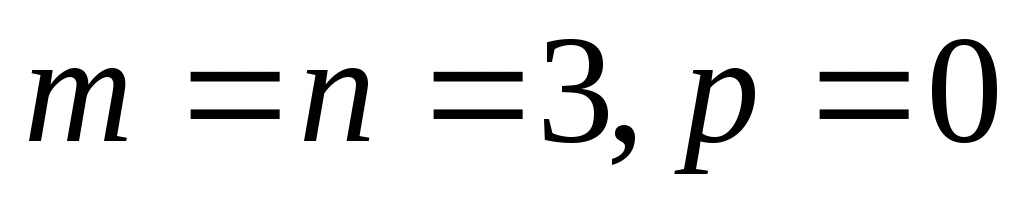 . Уравнение (32) принимает вид
. Уравнение (32) принимает вид
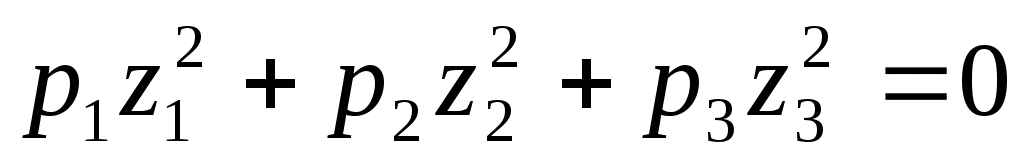 . Получаем случаи:
. Получаем случаи:
5)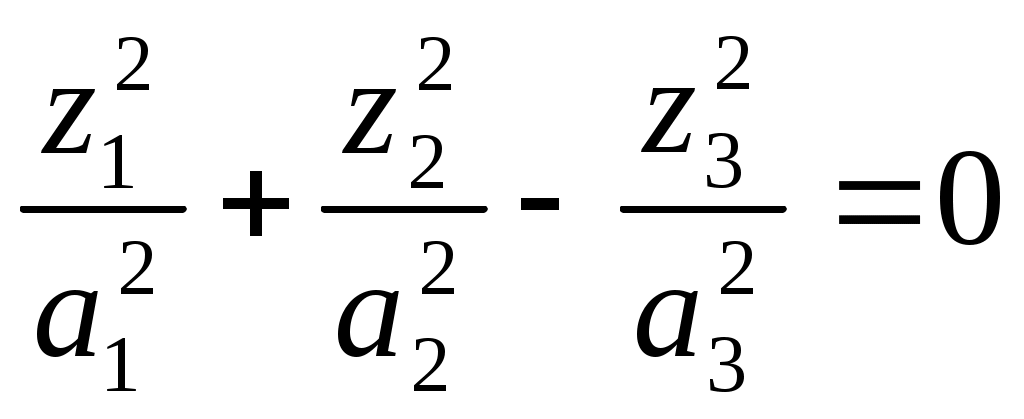 конус (при
конус (при 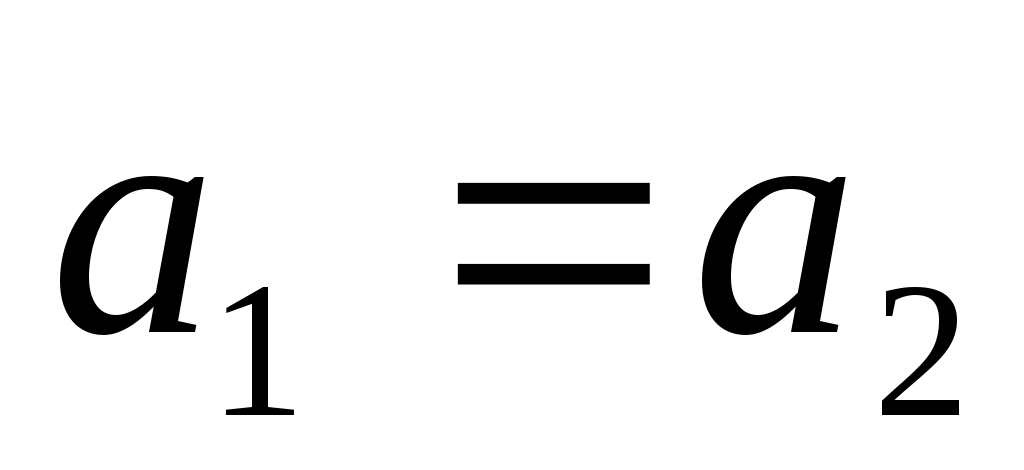 конус вращения);
конус вращения);
6)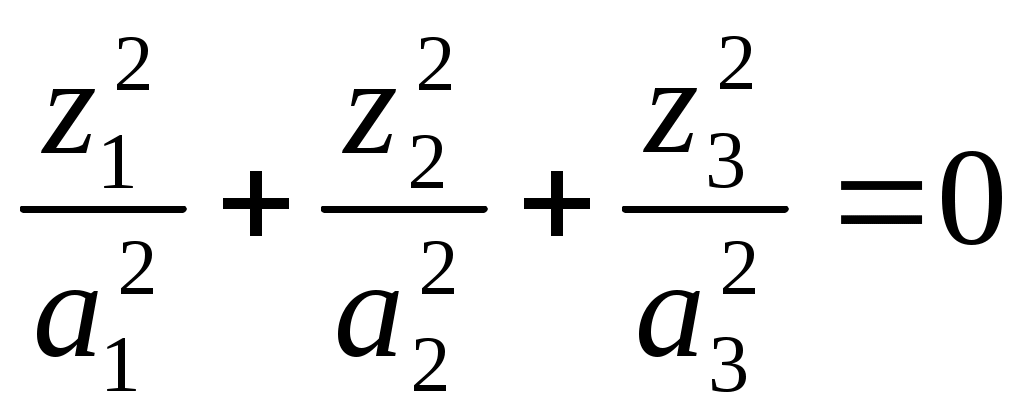 мнимый конус с вершиной в действительной точке;
мнимый конус с вершиной в действительной точке;
Случай 3.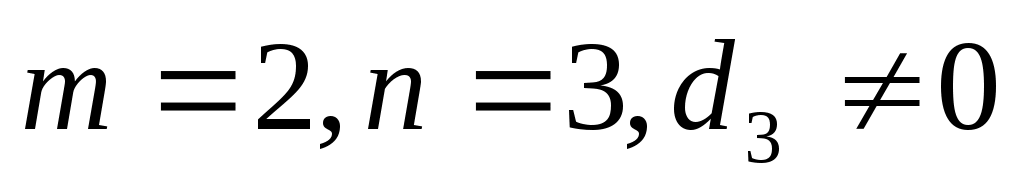 . Уравнение (32) принимает вид
. Уравнение (32) принимает вид
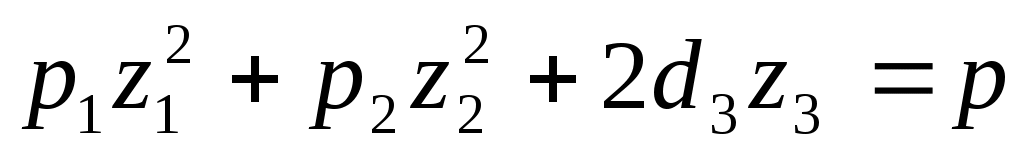 .
.
С помощью параллельного переноса координат по формулам
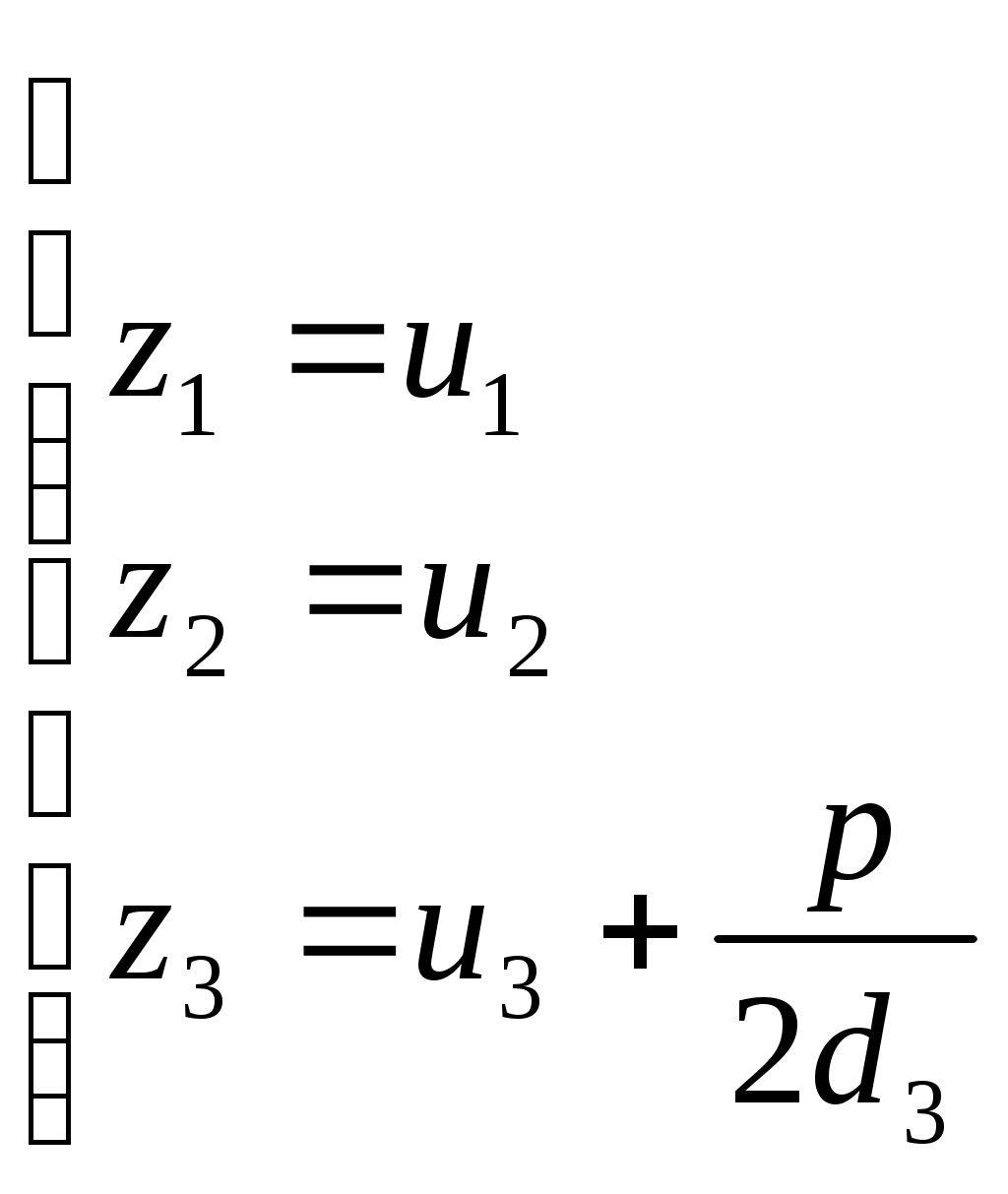
можно освободиться от свободного члена. Получим частные случаи:
7)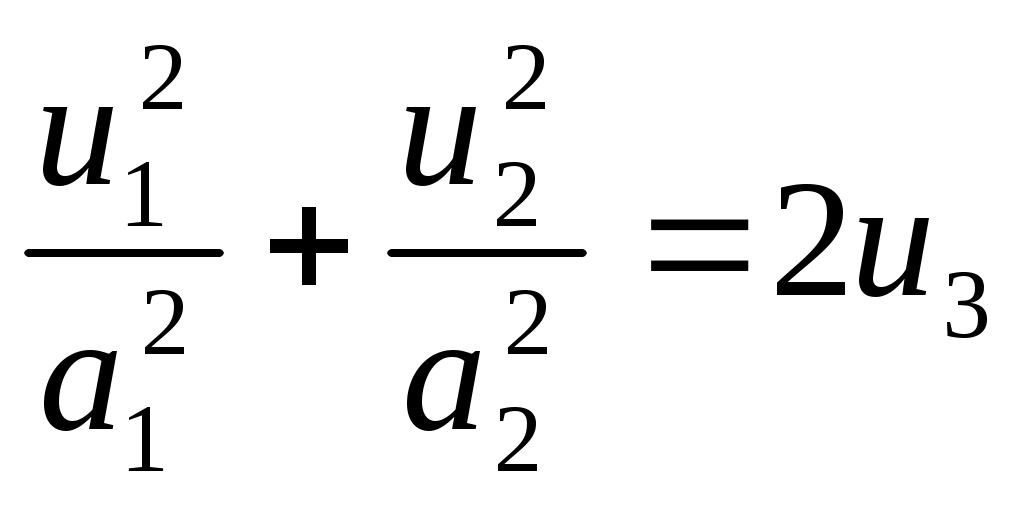
эллиптический параболоид (при параболоид вращения);
параболоид вращения);
8)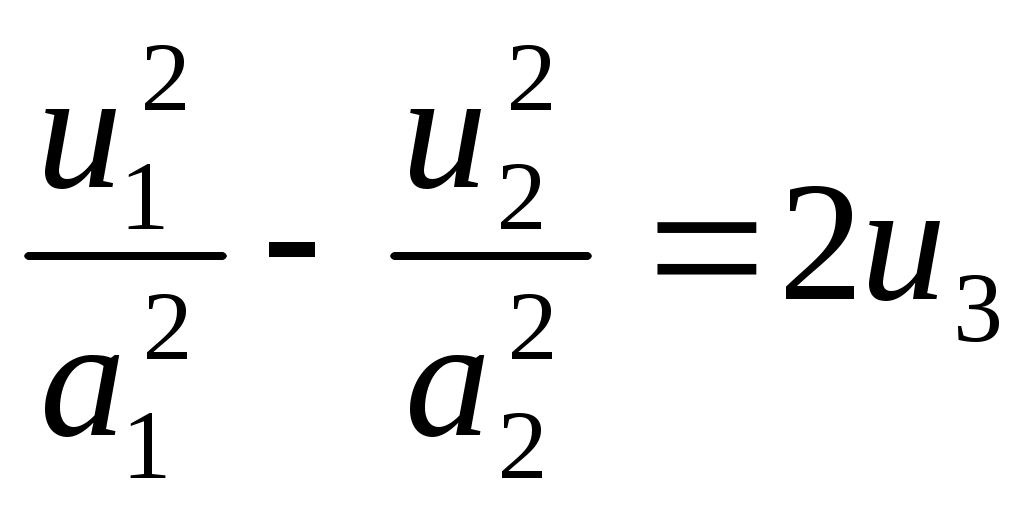 гиперболический параболоид.
гиперболический параболоид.
Случай 4. Цилиндрические квадрики.
1.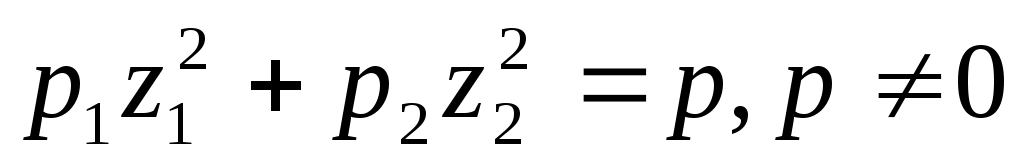 .
.
9)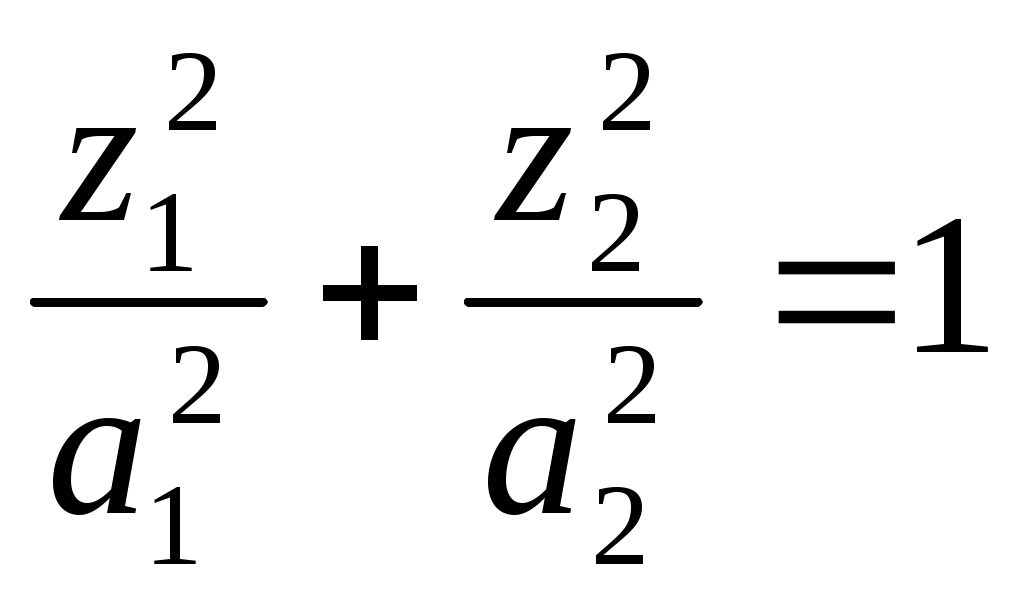 эллиптический цилиндр (при
эллиптический цилиндр (при  цилиндр вращения);
цилиндр вращения);
10)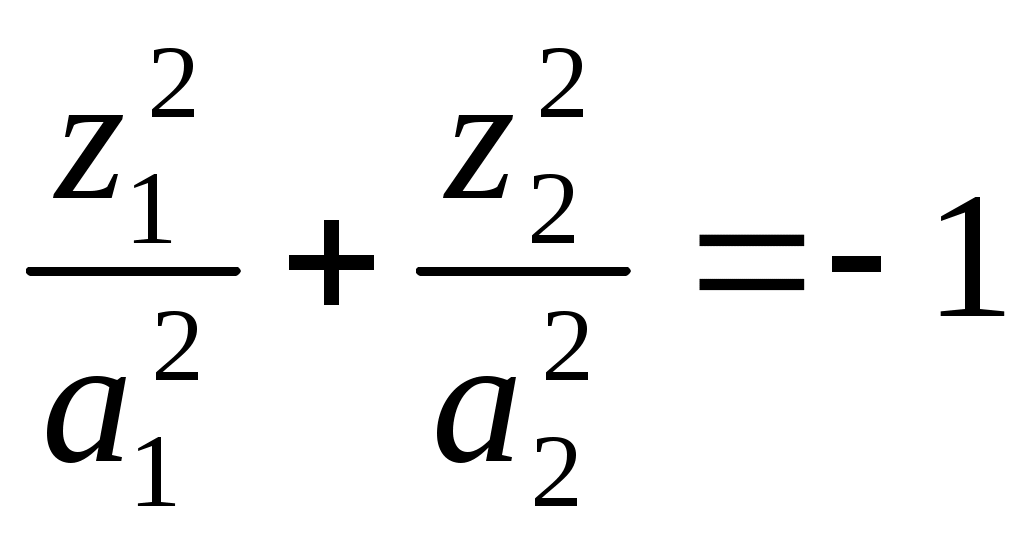 мнимый эллиптический цилиндр;
мнимый эллиптический цилиндр;
11)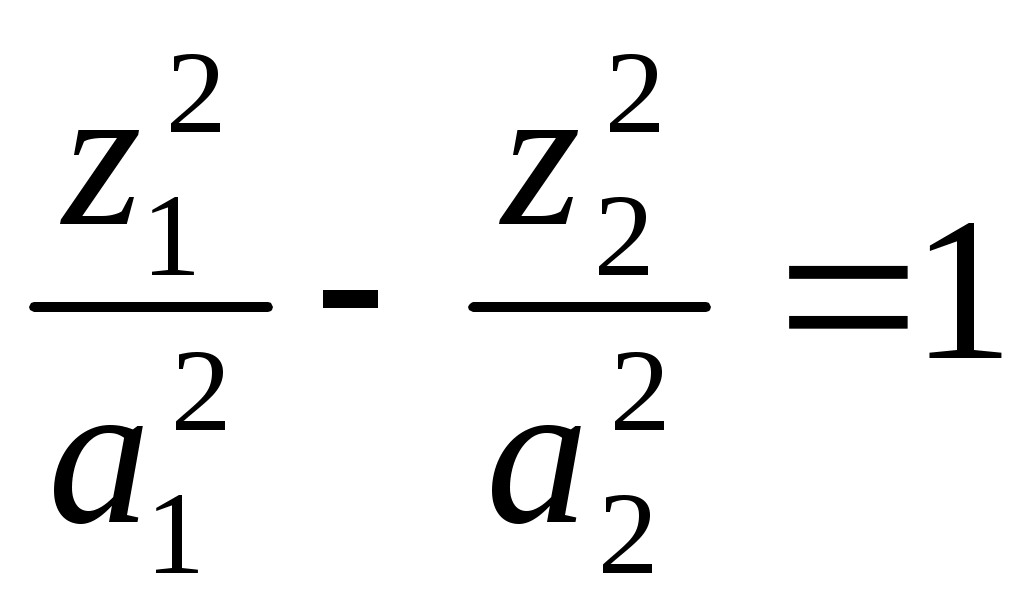 гиперболический цилиндр.
гиперболический цилиндр.
2.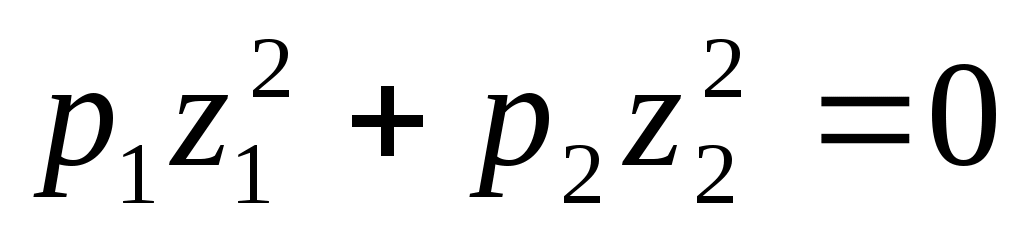 .
.
12)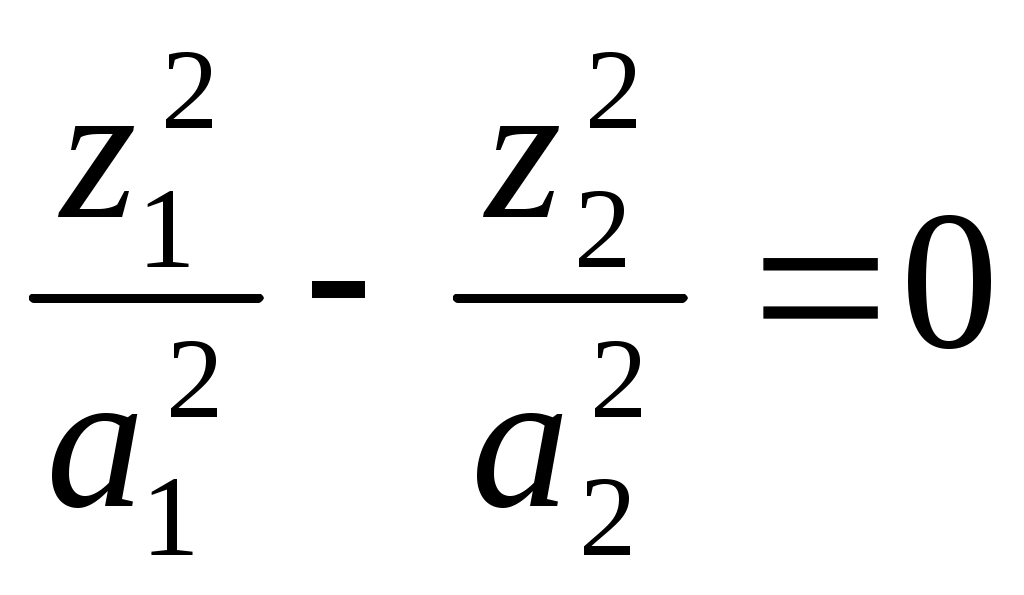 пара пересекающихся плоскостей;
пара пересекающихся плоскостей;
13)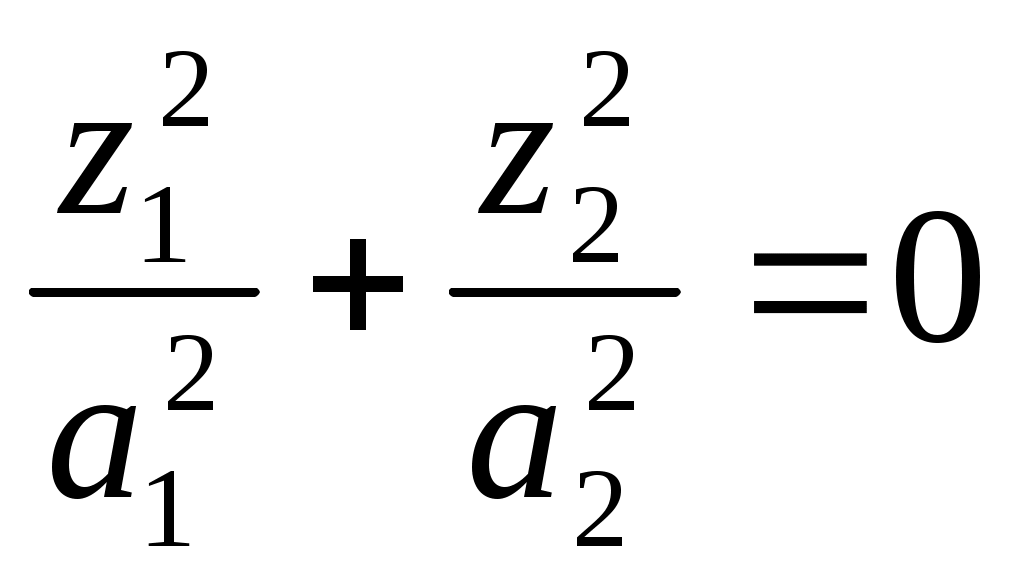 пара мнимых плоскостей, пересекающихся по действительной прямой
пара мнимых плоскостей, пересекающихся по действительной прямой
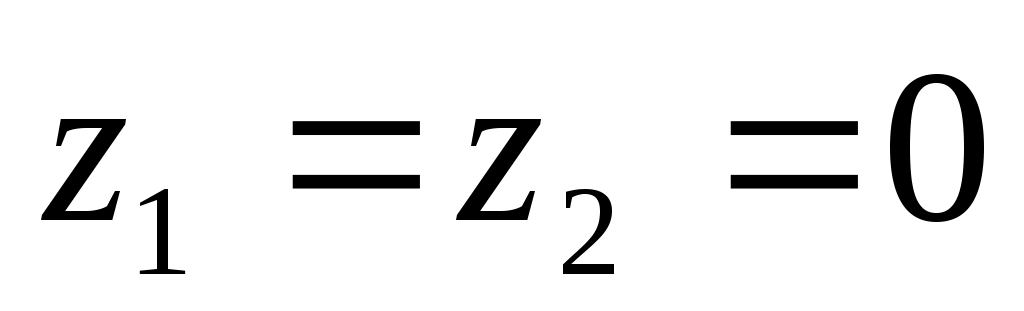 .
.
3.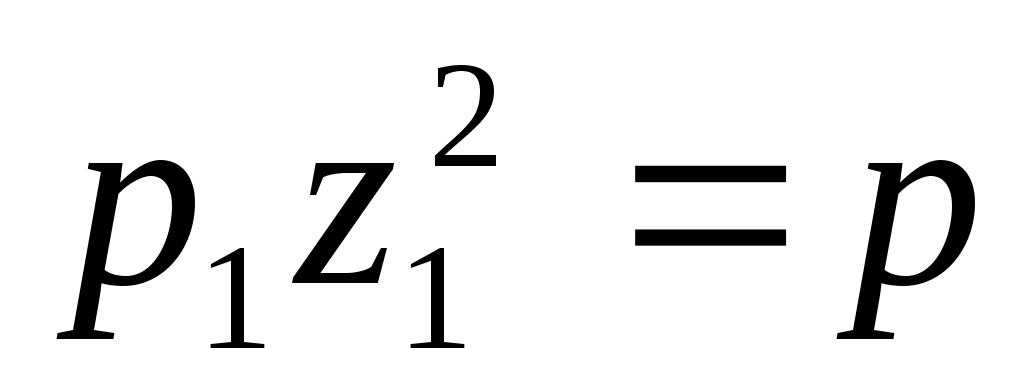 .
.
14)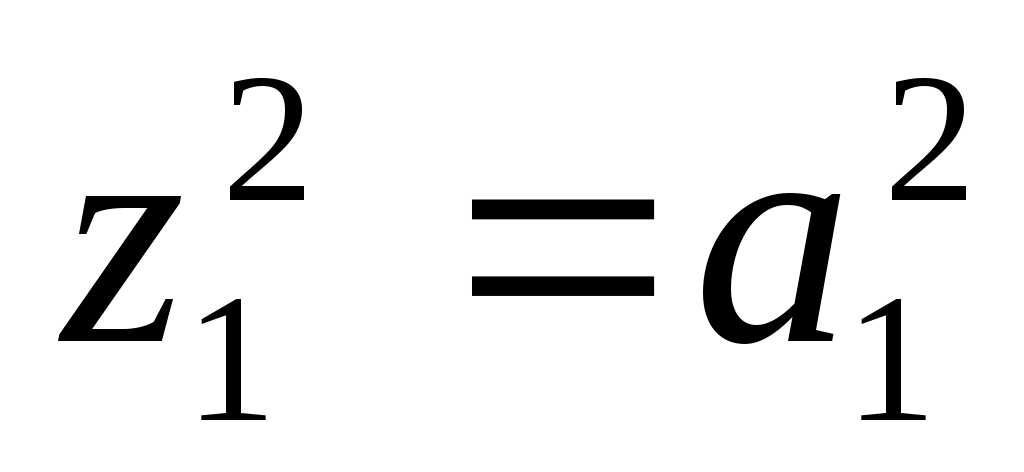 пара различных параллельных плоскостей;
пара различных параллельных плоскостей;
15)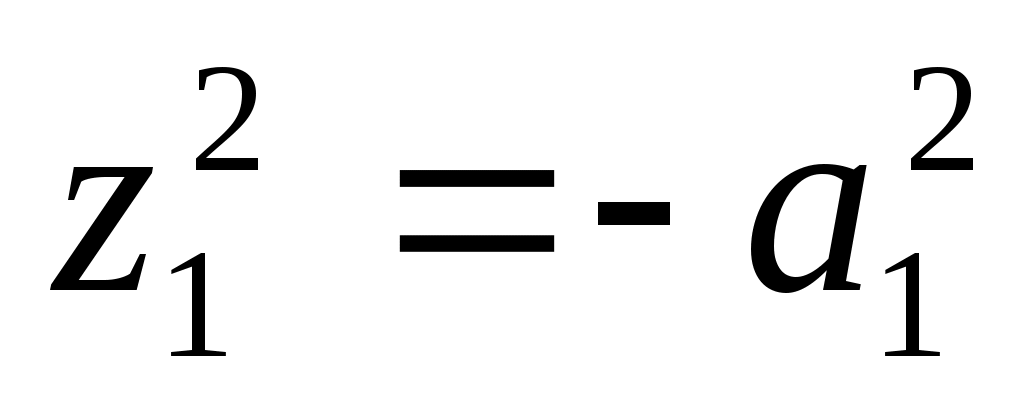 пара мнимых параллельных плоскостей;
пара мнимых параллельных плоскостей;
16)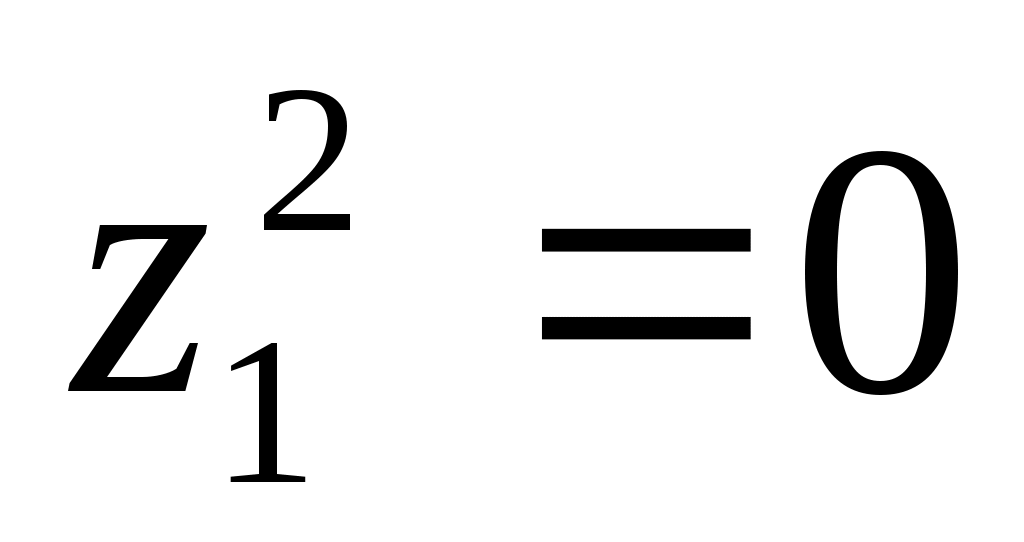 пара совпавших плоскостей.
пара совпавших плоскостей.
4.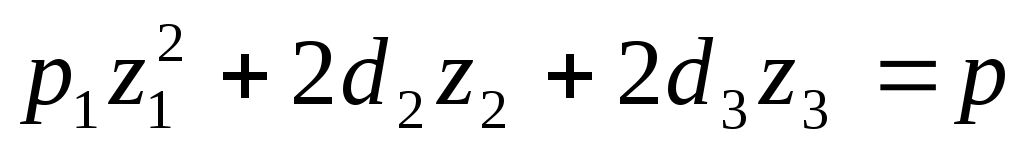 , где
, где 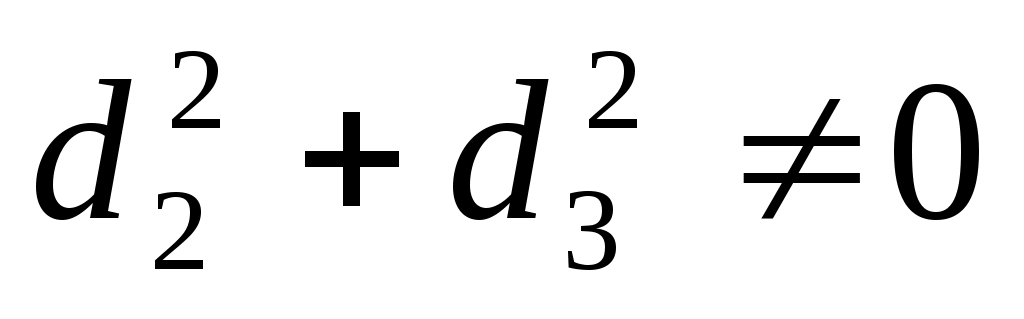 .
.
Разделив обе части этого уравнения на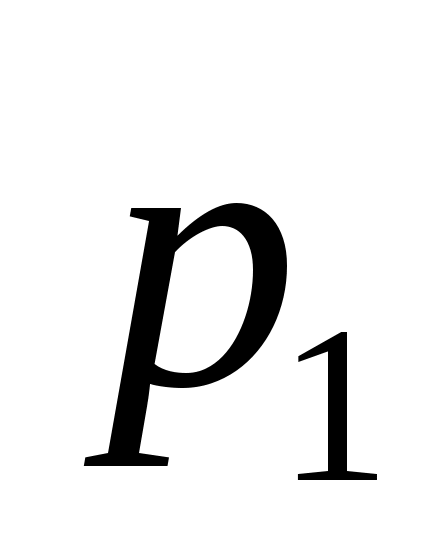 и освободившись, как в случае 3, от свободного члена, приходим к уравнению вида
и освободившись, как в случае 3, от свободного члена, приходим к уравнению вида
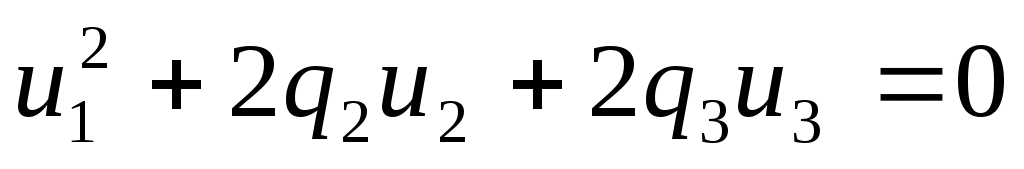 .
.
С помощью ортогонального преобразования
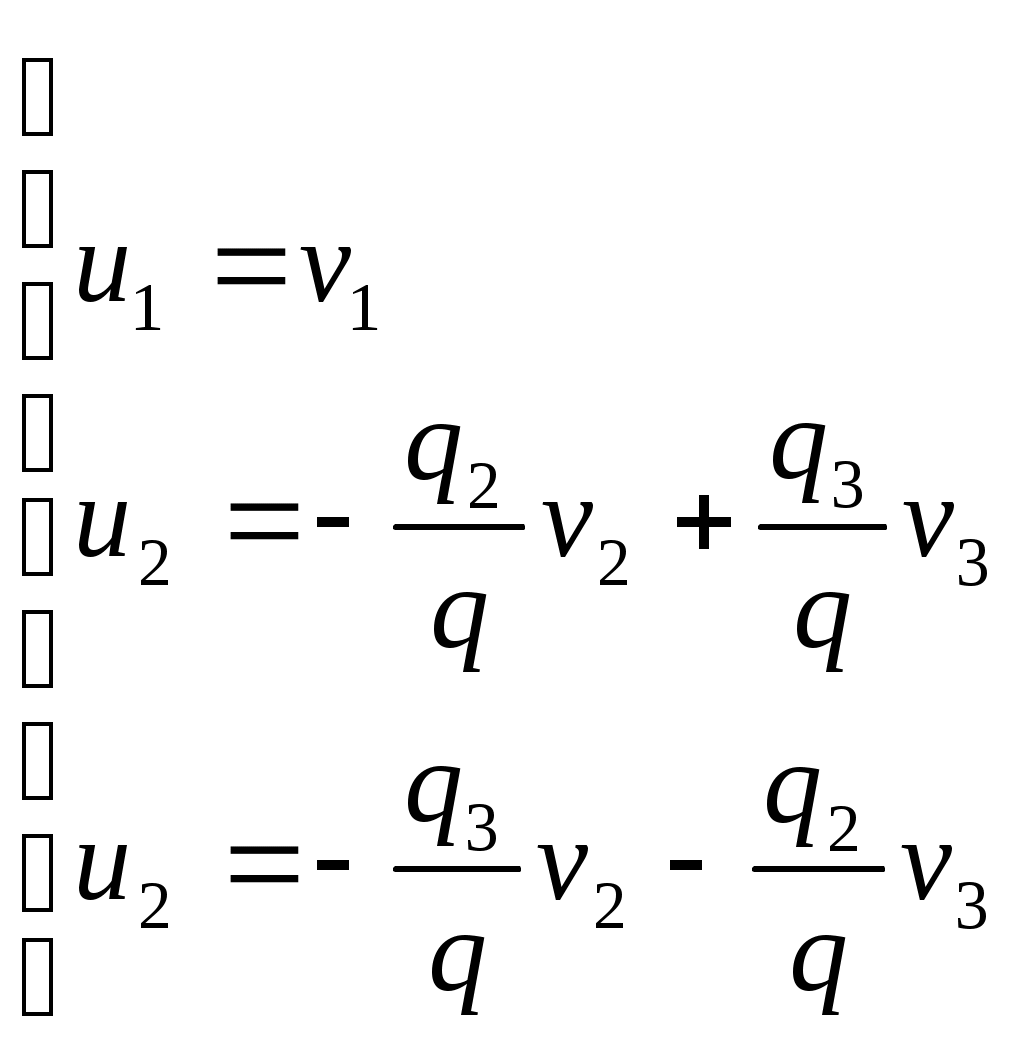
где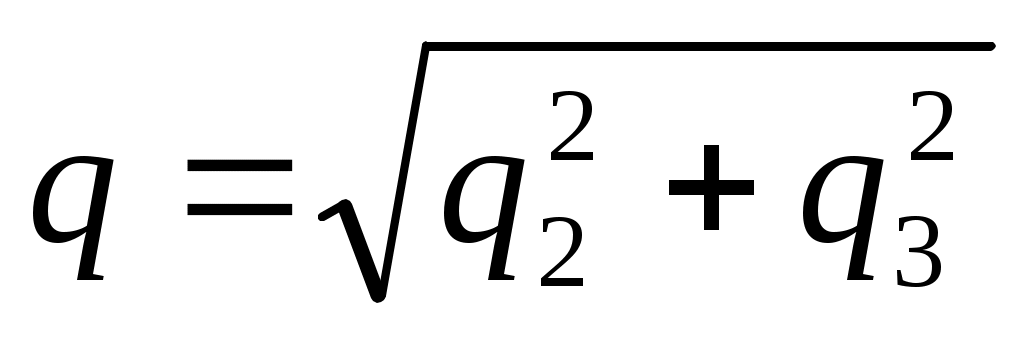 , переходим к новой прямоугольной декартовой системе координат, относительно которой квадрика параболический цилиндр будет иметь уравнение
, переходим к новой прямоугольной декартовой системе координат, относительно которой квадрика параболический цилиндр будет иметь уравнение
17)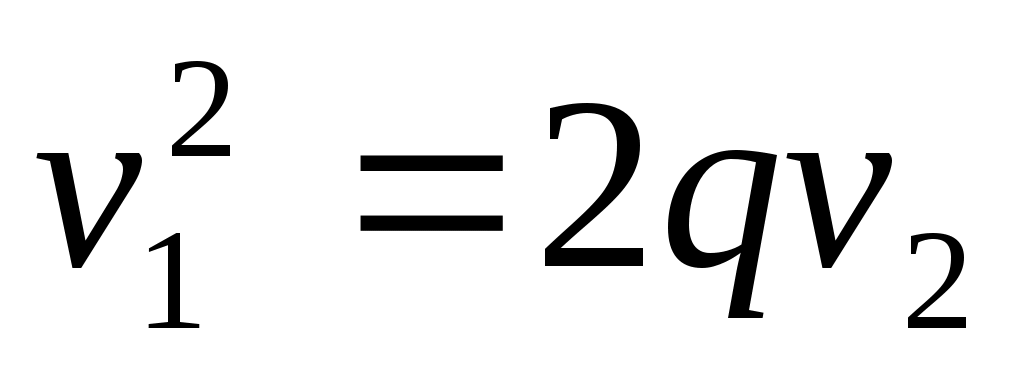 .
.
Те виды, к которым было приведено уравнение квадрики во всех рассмотренных выше случаях, называются
каноническимивидами уравнения квадрики.
Имеет место теорема о классификации квадрик в Е3: Существует семнадцать и только семнадцать поверхностей второго порядка (рассмотренных выше).
Теории симметричных и квадратичных форм векторных пространств и квадрик (или геометрических образов второго порядка) проективных пространств над полем развивались взаимосвязано и достаточно хорошо разработаны. Изучение произвольных рефлексивных форм над полем сведено к изучению невырожденных рефлексивных форм, а последние классифицированы вместе с симметричными и кососимметричными формами. Наряду с развитием этой теории, в исследованиях проективных пространств возрастал интерес к переходу от полей к более общим кольцам коэффициентов.
Естественно, что квадрики исследуются взаимосвязано с квадратичными формами и их матрицами.
В данной работе были рассмотрены квадратичные формы, их основные представления – нормальный и канонический вид. Доказана возможность приведения квадратичной формы к основным видам и указаны способы преобразования квадратичных форм.
Также рассмотрено понятие квадрики, центра квадрики и приведение уравнения квадрики к нормальному виду. В работу приведена классификация квадрики, в частности классификация в двумерном аффинном и трёхмерном евклидовом пространствах.
Объекты, которые мы рассмотрели, в частности аффинные квадрики, очень важны с практической точки зрения, ибо это самые простые, после прямых и плоскостей, поверхности и кривые в трёхмерном пространстве и на плоскости, которые встречаются всюду – в математике и механике, физике и астрономии. Верхушка Эйфелевой башни и верхние этажи Монпарнасской башни в ветреную погоду описывают эллипсы, у которых максимальная ось должна быть разумной величины, чтобы это не казалось опасным. А при помощи парабол проще всего выполнить сопряжение двух прямых. Поэтому теория квадратичных форм и квадрик всегда будет актуальна.
1. Атанасян Л.С., «Геометрия», часть 1. М.:»ПРОСВЕЩЕНИЕ», 1973 г.;
2. М.Берже, «Геометрия», том 2. М.: «Мир», 1984;
3. Ефимов Н.В., Розендорн Э.Р., «Линейная алгебра и многомерная геометрия». – М. 1970 г.;
4. Парнасский И.В., Парнасская О.Е., «Многомерные пространства. Квадратичные формы и квадрики». – М.: «ПРОСВЕЩЕНИЕ», 1978 г..
Чтобы дать полную классификацию квадрик при п = 3, рассмотрим все частные случаи, которые могут представиться при упрощении уравнения (32).
Случай 1.
В зависимости от знаков
1)
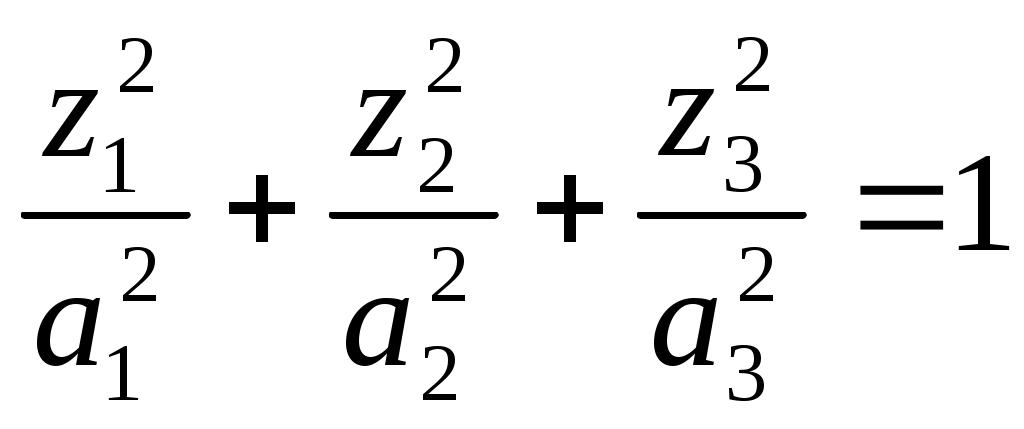 эллипсоид;
эллипсоид;2)
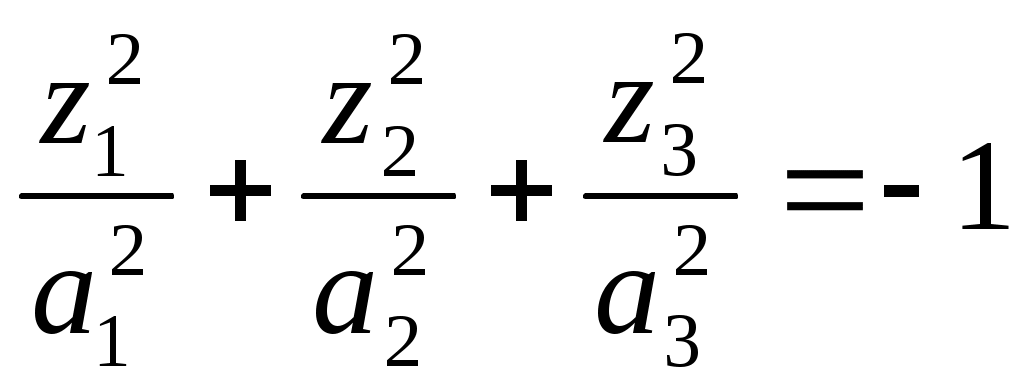 мнимый эллипсоид;
мнимый эллипсоид;3)
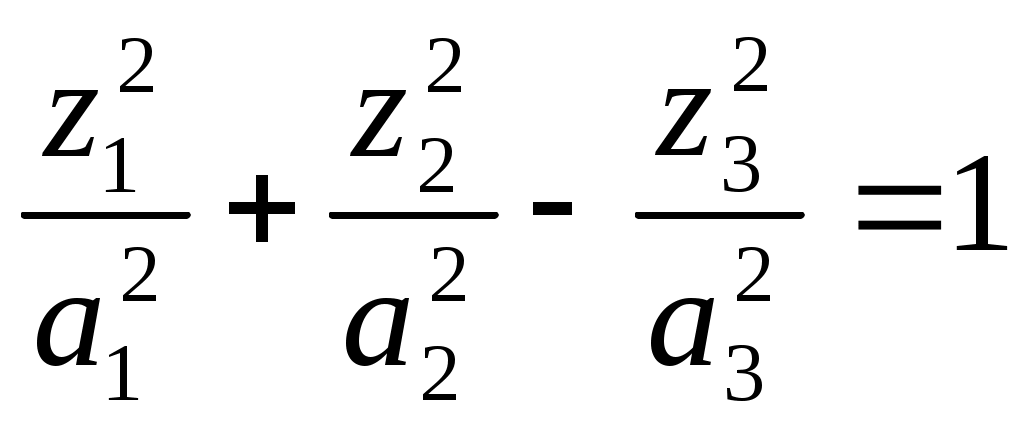 однополостный гиперболоид;
однополостный гиперболоид;4)
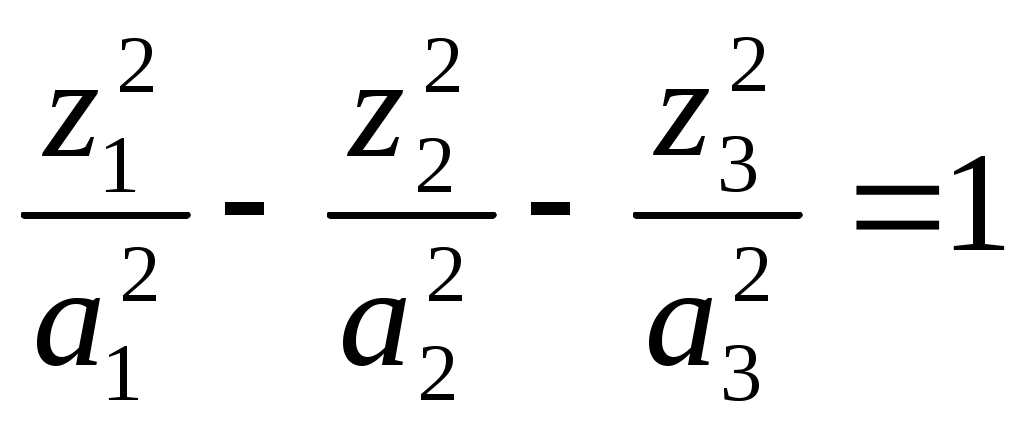 двуполостный гиперболоид.
двуполостный гиперболоид.Все эллипсоиды аффинно эквивалентны и, следовательно, с точки зрения аффинной геометрии не отличаются друг от друга по своим свойствам. Однако не всякие два эллипсоида конгруэнтны и даже подобны; в связи с этим в евклидовой геометрии появляется возможность классификации эллипсоидов.
Если а1, а2, а3 различны, то эллипсоид называется трехосным. Если равны какие-нибудь два из чисел
а1, а2, а3, то эллипсоид называется эллипсоидом вращения. Если а1 = а2 = а3, то эллипсоид является сферой. Эта классификация инвариантна относительно движений; например, любое движение может отобразить сферу также только на сферу. Поэтому указанные виды эллипсоидов являются объектами, изучаемыми в евклидовой геометрии.
Аналогичные замечания можно сделать и относительно других видов квадрик(например, можно выделить гиперболоиды вращения, конус вращения и т. п.).
Случай 2.
5)
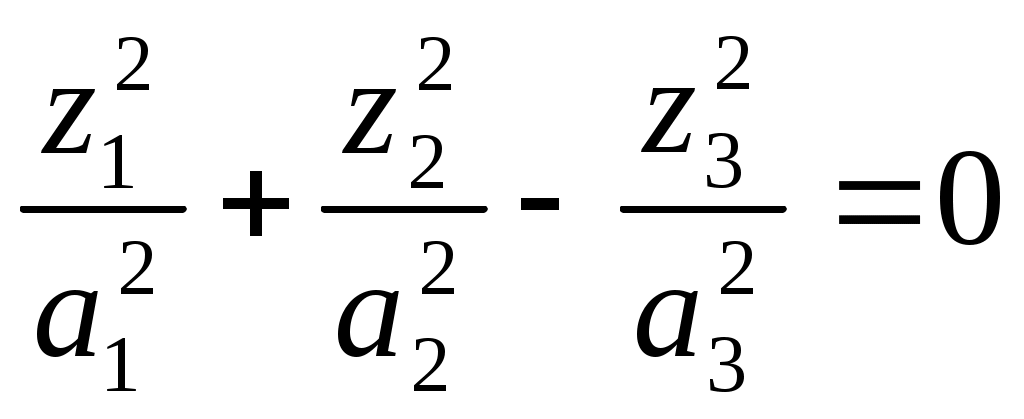 конус (при
конус (при 6)
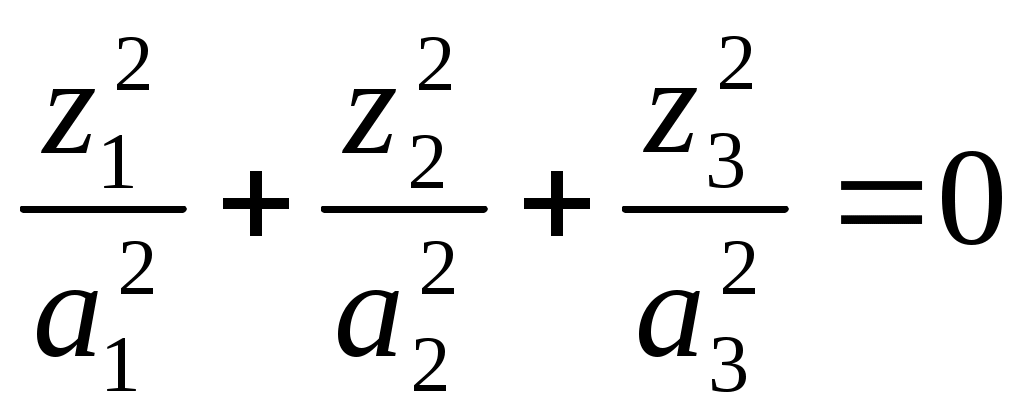 мнимый конус с вершиной в действительной точке;
мнимый конус с вершиной в действительной точке;Случай 3.
С помощью параллельного переноса координат по формулам
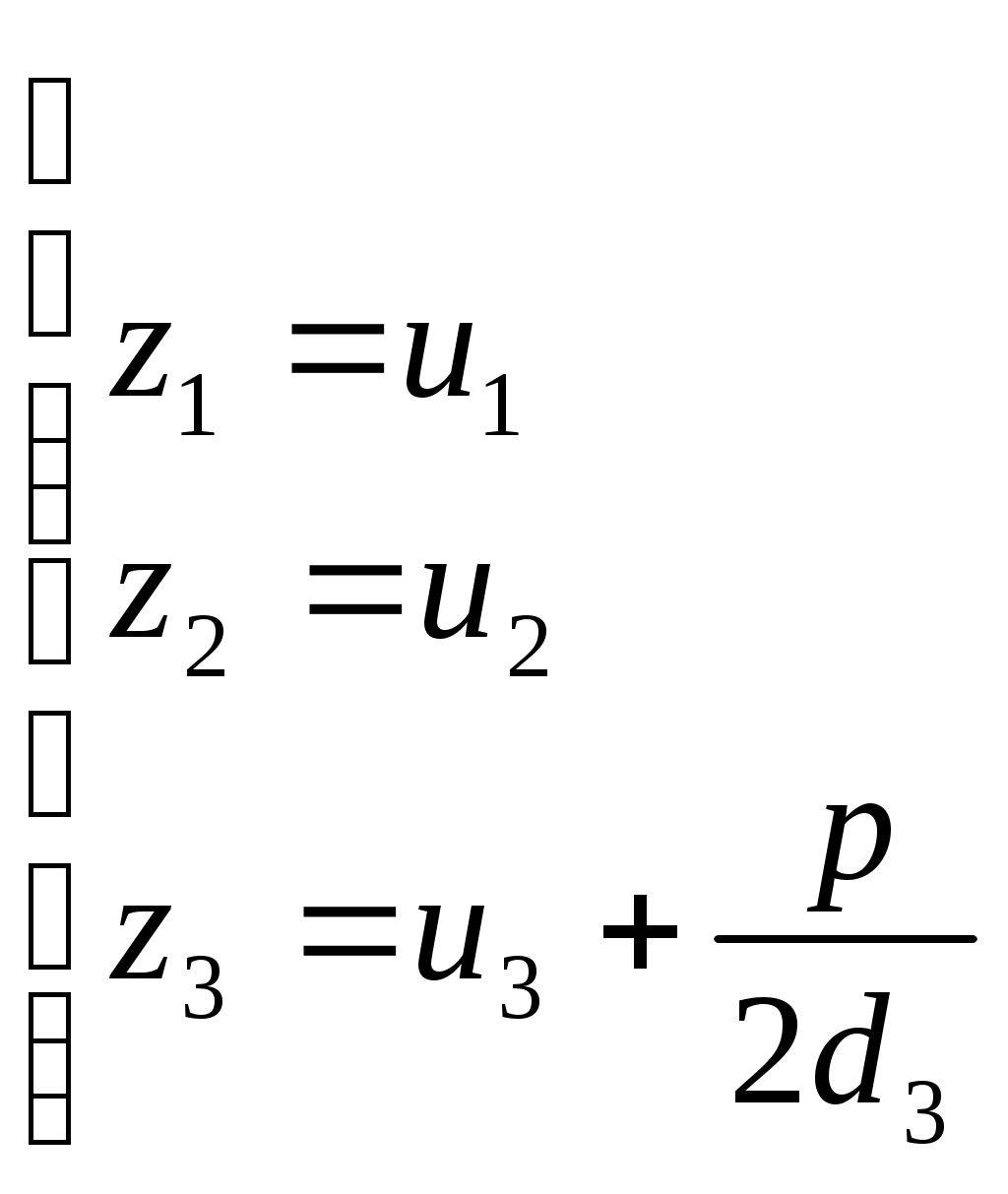
можно освободиться от свободного члена. Получим частные случаи:
7)
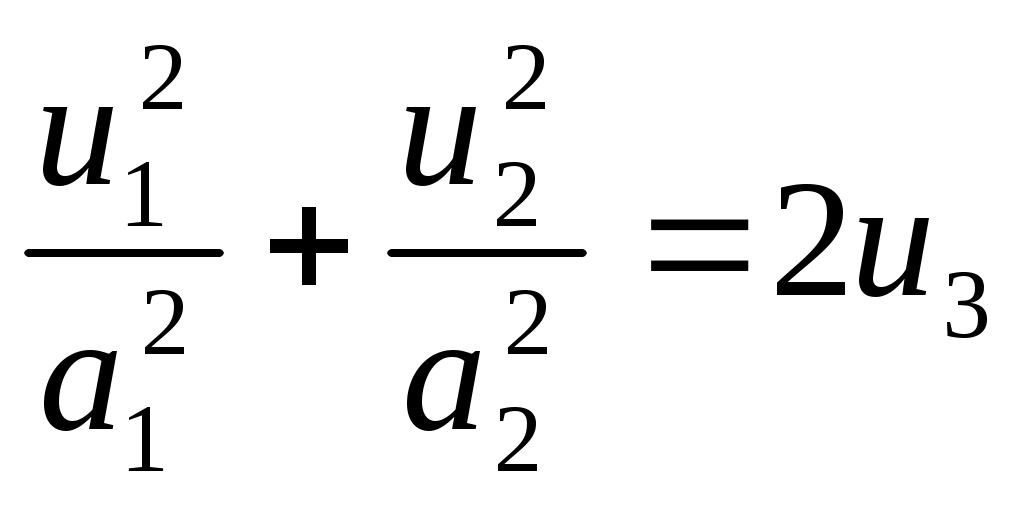
эллиптический параболоид (при
8)
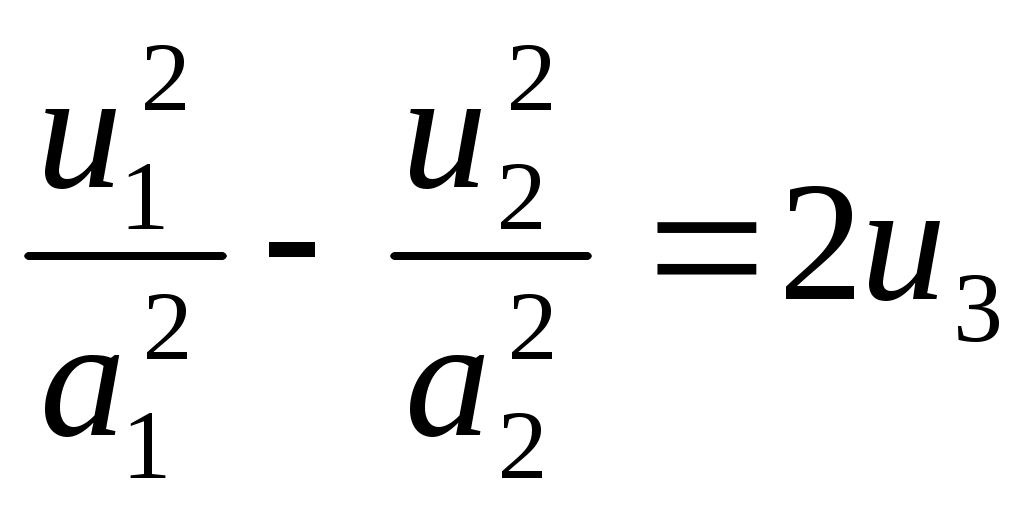 гиперболический параболоид.
гиперболический параболоид.Случай 4. Цилиндрические квадрики.
1.
9)
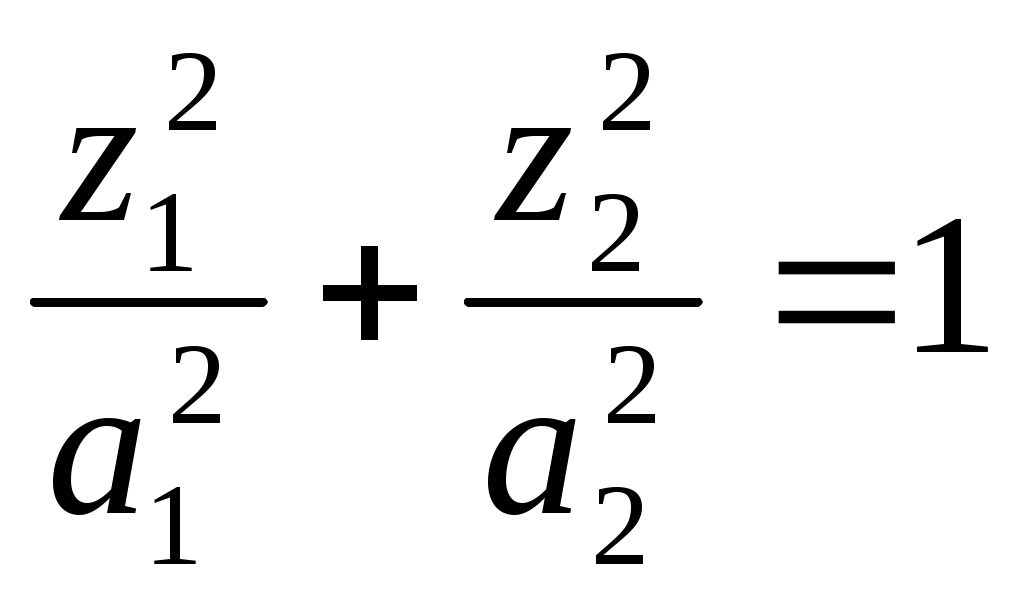 эллиптический цилиндр (при
эллиптический цилиндр (при 10)
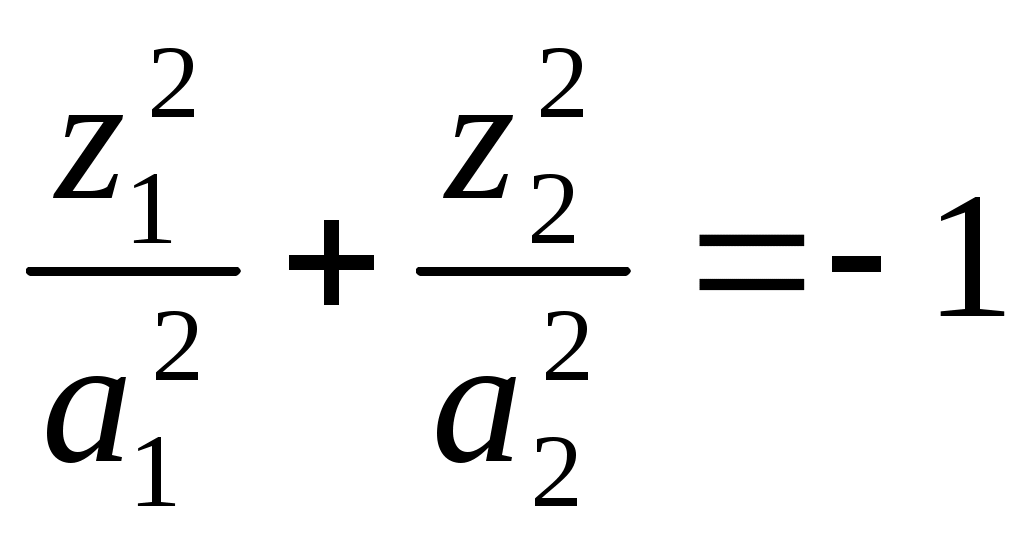 мнимый эллиптический цилиндр;
мнимый эллиптический цилиндр;11)
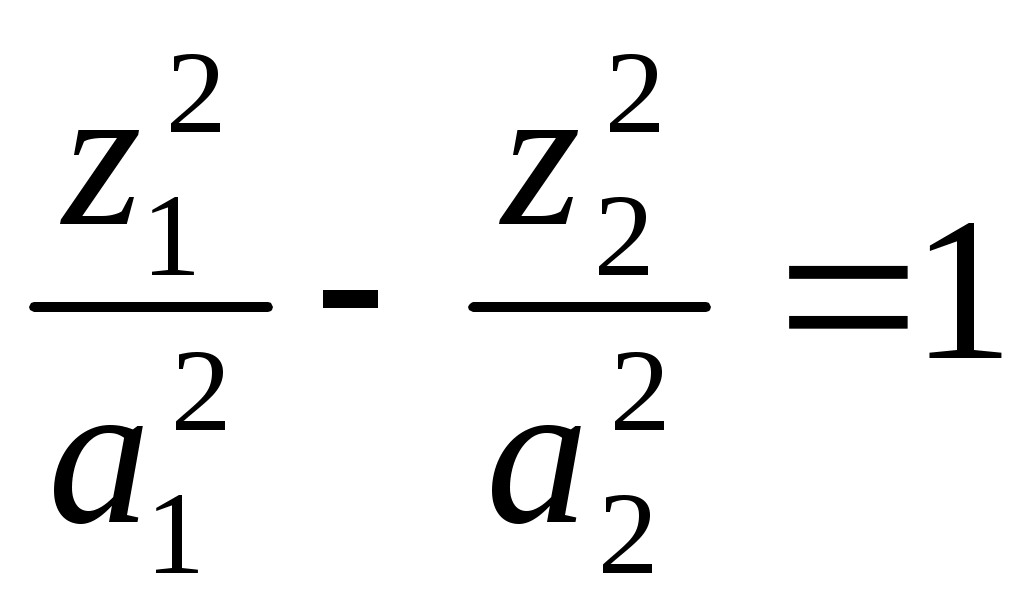 гиперболический цилиндр.
гиперболический цилиндр.2.
12)
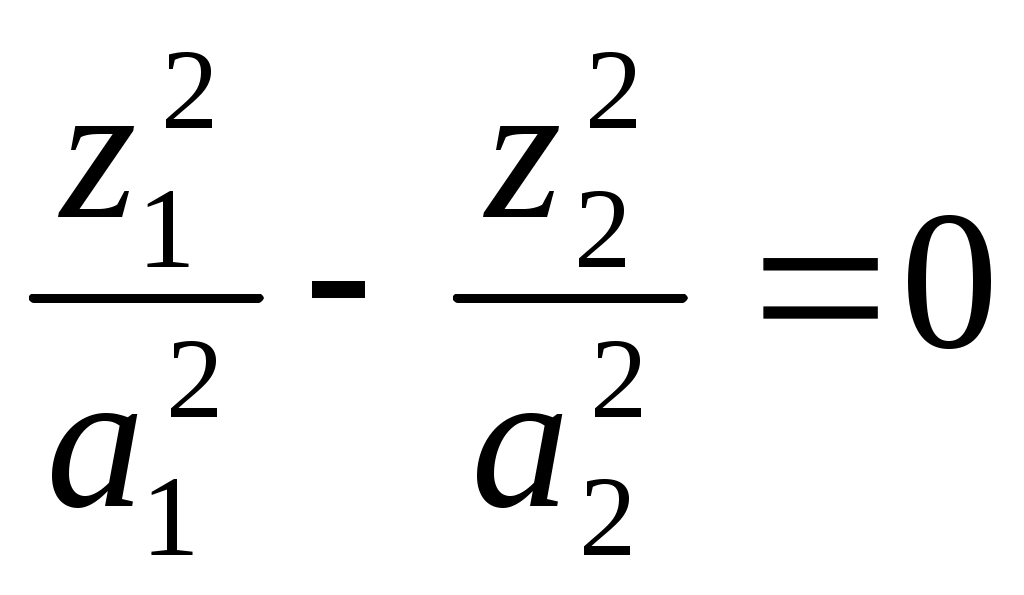 пара пересекающихся плоскостей;
пара пересекающихся плоскостей;13)
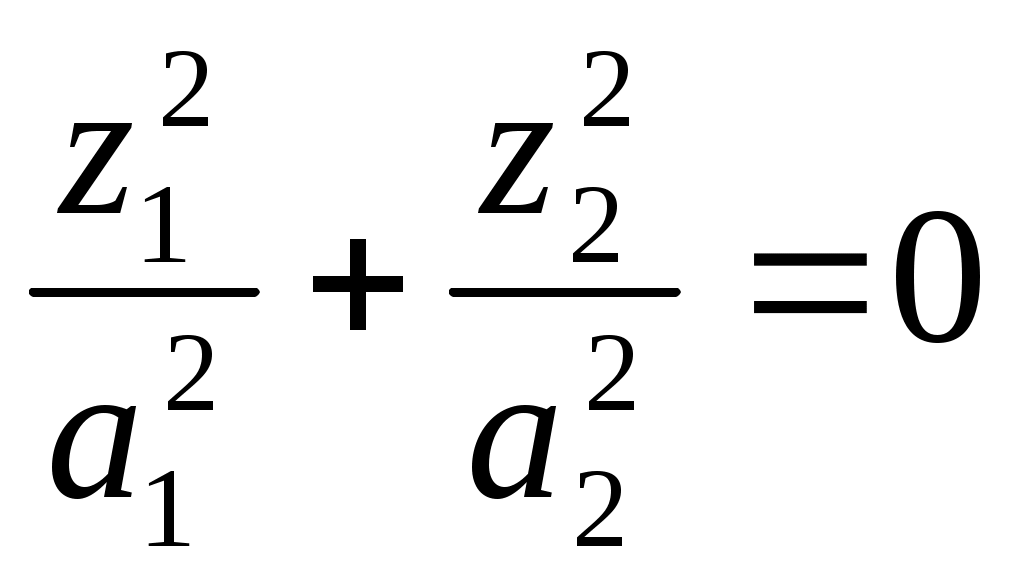 пара мнимых плоскостей, пересекающихся по действительной прямой
пара мнимых плоскостей, пересекающихся по действительной прямой
3.
14)
15)
16)
4.
Разделив обе части этого уравнения на
С помощью ортогонального преобразования
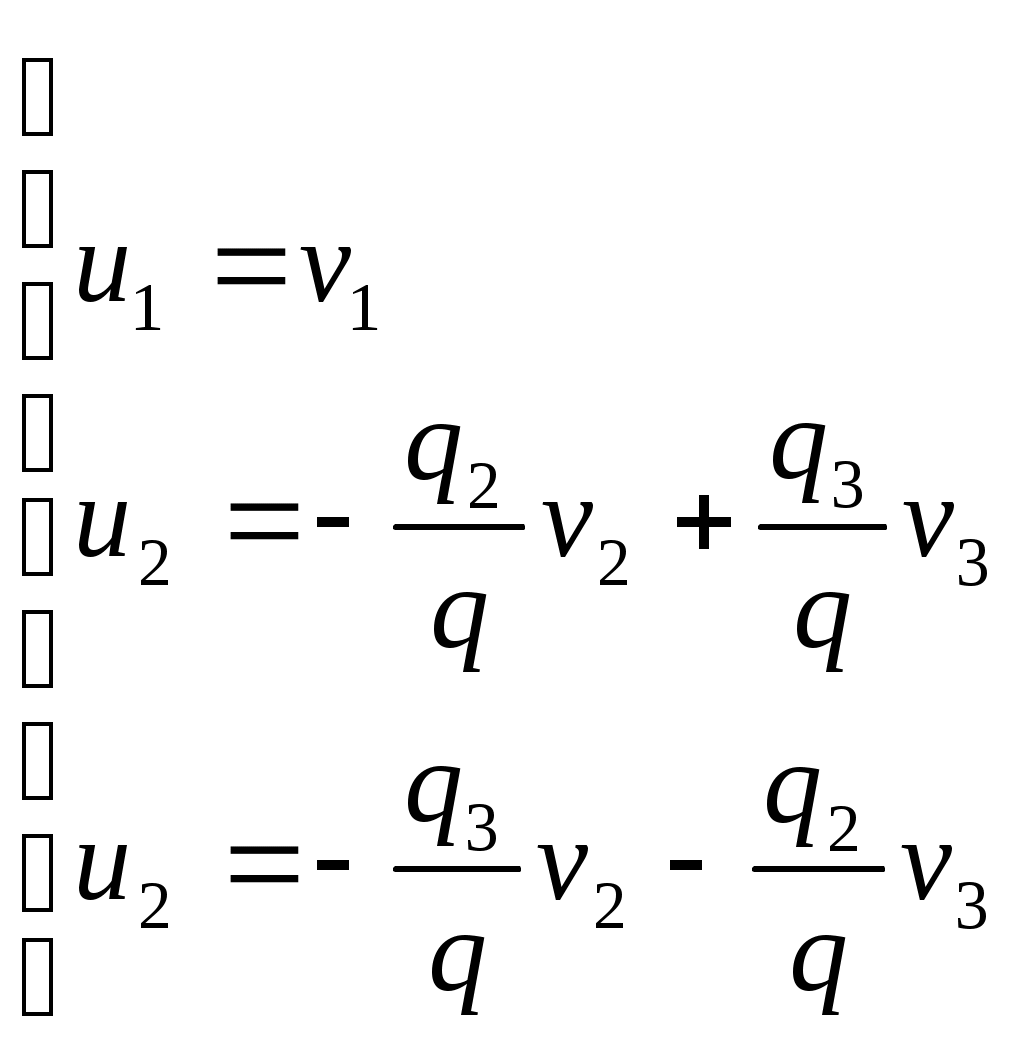
где
17)
Те виды, к которым было приведено уравнение квадрики во всех рассмотренных выше случаях, называются
каноническимивидами уравнения квадрики.
Имеет место теорема о классификации квадрик в Е3: Существует семнадцать и только семнадцать поверхностей второго порядка (рассмотренных выше).
ЗАКЛЮЧЕНИЕ.
Теории симметричных и квадратичных форм векторных пространств и квадрик (или геометрических образов второго порядка) проективных пространств над полем развивались взаимосвязано и достаточно хорошо разработаны. Изучение произвольных рефлексивных форм над полем сведено к изучению невырожденных рефлексивных форм, а последние классифицированы вместе с симметричными и кососимметричными формами. Наряду с развитием этой теории, в исследованиях проективных пространств возрастал интерес к переходу от полей к более общим кольцам коэффициентов.
Естественно, что квадрики исследуются взаимосвязано с квадратичными формами и их матрицами.
В данной работе были рассмотрены квадратичные формы, их основные представления – нормальный и канонический вид. Доказана возможность приведения квадратичной формы к основным видам и указаны способы преобразования квадратичных форм.
Также рассмотрено понятие квадрики, центра квадрики и приведение уравнения квадрики к нормальному виду. В работу приведена классификация квадрики, в частности классификация в двумерном аффинном и трёхмерном евклидовом пространствах.
Объекты, которые мы рассмотрели, в частности аффинные квадрики, очень важны с практической точки зрения, ибо это самые простые, после прямых и плоскостей, поверхности и кривые в трёхмерном пространстве и на плоскости, которые встречаются всюду – в математике и механике, физике и астрономии. Верхушка Эйфелевой башни и верхние этажи Монпарнасской башни в ветреную погоду описывают эллипсы, у которых максимальная ось должна быть разумной величины, чтобы это не казалось опасным. А при помощи парабол проще всего выполнить сопряжение двух прямых. Поэтому теория квадратичных форм и квадрик всегда будет актуальна.
ЛИТЕРАТУРА.
1. Атанасян Л.С., «Геометрия», часть 1. М.:»ПРОСВЕЩЕНИЕ», 1973 г.;
2. М.Берже, «Геометрия», том 2. М.: «Мир», 1984;
3. Ефимов Н.В., Розендорн Э.Р., «Линейная алгебра и многомерная геометрия». – М. 1970 г.;
4. Парнасский И.В., Парнасская О.Е., «Многомерные пространства. Квадратичные формы и квадрики». – М.: «ПРОСВЕЩЕНИЕ», 1978 г..

