Файл: Основная часть. 4 I. Квадратичные формы..doc

Доказательство. Воспользуемся методом математической индукции. Квадратичная форма от одной переменной x_i имеет вид c₁₁x₁², уже являющийся каноническим. Предположим, что эта теорема верна для квадратичных форм от переменных, и докажем, что она будет верна тогда и для квадратичных форм от n переменных.

Если квадратичная форма (3) не содержит квадратов переменных, то по лемме 1 ее можно с помощью линейного преобразования перевести и в квадратичную форму, содержащую квадрат хотя бы одной переменной. По лемме 2 полученную квадратичную форму можно представить в виде (4). Т.к. квадратичная форма g в равенстве (4) зависит от переменных , то по сделанному предположению она может быть приведена к каноническому виду линейным преобразованием этих переменных. От переменных мы перейдем при этом к новым переменным . Если к формулам этого перехода добавить еще и формулу , то получатся формулы линейного преобразования, которое приводит к каноническому виду квадратичную форму , содержащуюся в равенстве (4).

Композиция всех рассмотренных преобразований переменных является искомым линейным преобразованием, приводящим к каноническому виду данную квадратичную форму (3).

Если квадратичная форма (3) содержит квадрат какой-нибудь переменной, то лемму 1 применять не нужно. Теорема доказана.

Способы приведения квадратичной формы к каноническому и нормальному виду.

1) Если данная квадратичная форма от n переменных не содержит квадратов переменных, то с помощью линейного преобразования, примененного при доказательстве леммы 1, переходим к квадратичной форме, содержащей квадраты переменных. Затем с помощью линейного преобразования, рассмотренного при доказательстве

---

леммы 2, представляем квадратичную форму в виде суммы члена с квадратом какой-нибудь переменной и квадратичной формы от остальных переменных. Применив снова этот же прием к полученной квадратичной форме, получаем еще один член с квадратом другой переменной и квадратичную форму от остальных переменных. Этот процесс продолжаем до тех пор, пока не получится квадратичная форма, содержащая только члены с квадратами переменных.

От канонического вида квадратичной формы

,

где и отличны от нуля, можно перейти к нормальному виду



(где при с_i>0 и при с_i<0) с помощью линейного преобразования



Этот способ приведения квадратичной формы к нормальному виду называют методом Лагранжа.

2) Иногда трудно следовать алгоритму Лагранжа, например, ес­ли число неизвестных достаточно велико. Тогда можно восполь­зоваться методом Якоби.

Рассмотрим матрицу A квадратичной формы f

.

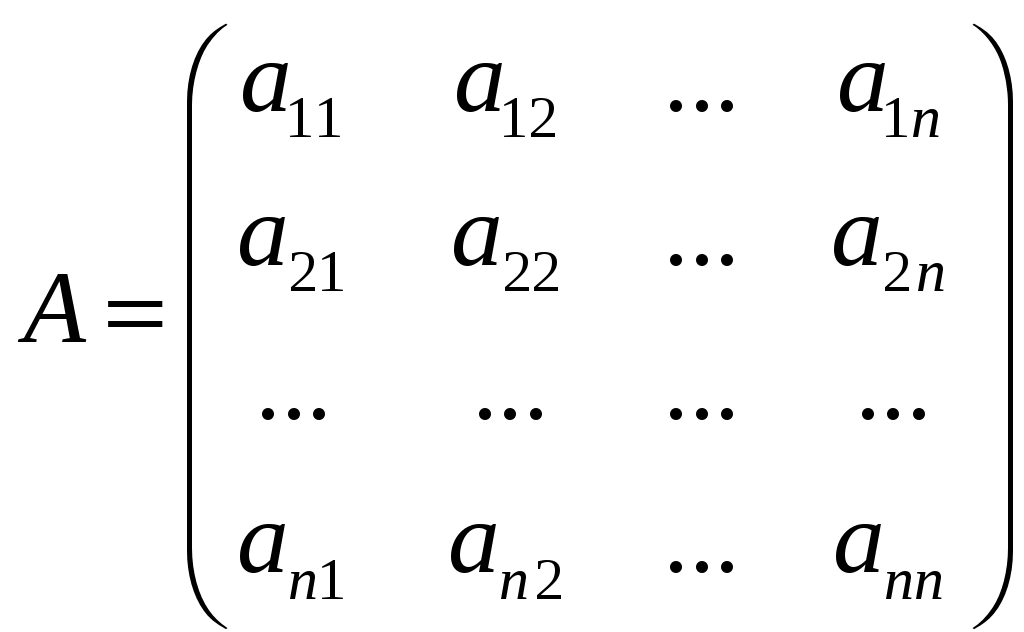Вычислим так называемые главные определители

.

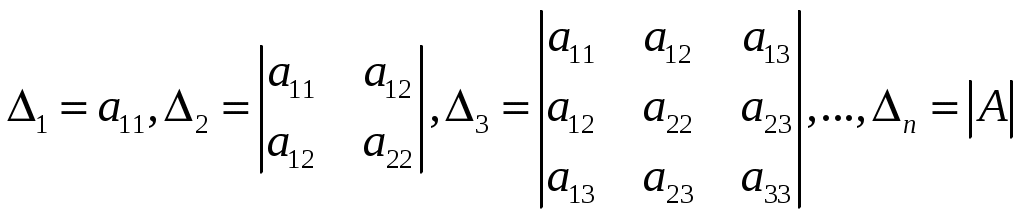Метод Якоби применим, если

При выполнении этого условия квадратичную форму f можно привести к одному из следующих видов:

или .

От первого вида ко второму можно перейти заменой неизвестных

---

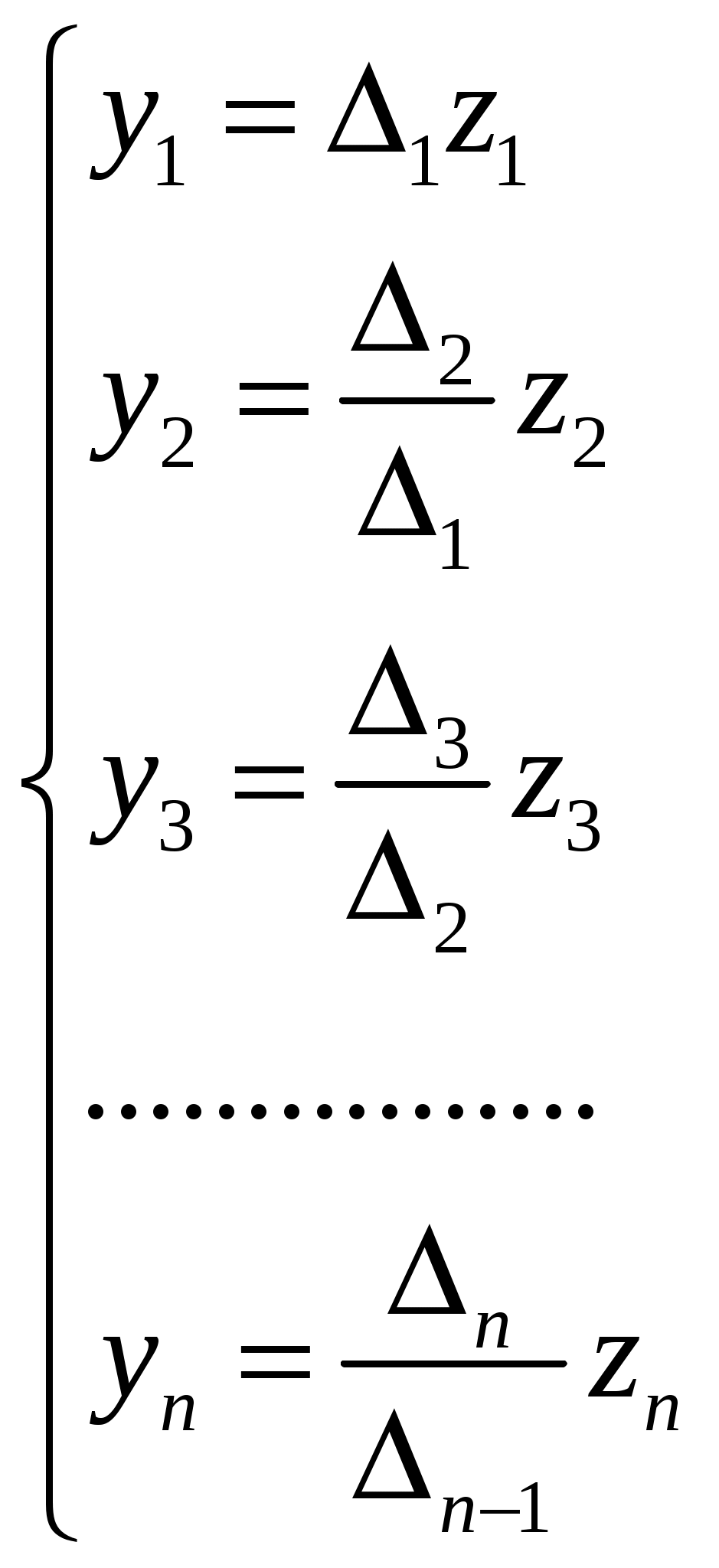
Закон инерции: Если данная квадратичная форма приведена к каноническому виду с помощью двух различных линейных преобразований, то число положительных коэффициентов при квадратах новых переменных, так же как и число отрицательных коэффициентов, будет в обоих случаях одно и то же (примем без доказательства).

3.Положительно определённые квадратичные формы.

Из закона инерции следует, что число р положительных, число q отрицательных, а значит, и число р+q всех ненулевых членов в каноническом виде квадратичной формы не зависит от способа приведения этой формы к каноническому виду.

Число всех ненулевых членов в каноническом виде квадратичной формы называется рангом этой формы, а число положительных членов – ее положительным индексом.

Можно доказать, что, к каким бы переменным ни была отнесена квадратичная форма, ранг этой формы и ранг ее матрицы одинаковы.

Квадратичная форма называется положительно определенной, если при любых одновременно не равных нулю значениях переменных ее значения положительны.

Теорема. Для того, чтобы квадратичная форма от n переменных была положительно определенной, необходимо и достаточно, чтобы ее положительный индекс был равен n.

Доказательство. Пусть квадратичная форма приведена к каноническому виду



с помощью линейных преобразований

(7)

Т.к. преобразование, обратное линейному, является линейным, то, решая систему уравнений (7) v_i, получим

(8)

Если  какие-нибудь значения старых переменных, не все равные нулю, то и соответствующие им значения новых переменных не все равны нулю. Действительно, если предположить, что

---

, то, подставляя эти значения в формулу (7), получим, что . Аналогично, если не все равны нулю, то согласно формуле (8) также и не все равны нулю. Для этих значений

(9)

Докажем теперь необходимость условия. Пусть квадратичная форма положительно определенная. Если положить



То из (9) следует, что . Так как квадратичная форма положительно определенная, то , а следовательно, и c₁>0. Аналогично получим, что c₂ >0, … , c_n >ни0, но это и означает, что положительный индекс данной квадратичной формы равен n.

Докажем то, что условие является также и достаточным. Пусть положительный индекс квадратичной формы равен n, т.е. c₁>0, c₂>0, … , c_n>0. Для любых значений , одновременно не равных нулю, соответствующие значения также не все равны нулю, но тогда из 20 следует, что , т.е. что квадратичная форма положительно определенная. Теорема доказана.

4. Квадратичные формы в евклидовом пространстве.

Определение. Линейное преобразование переменных с ортогональной матрицей называется ортогональным.

Квадратичную форму можно привести к каноническому виду, ограничиваясь только ортогональными преобразованиями переменных. Однако приведение квадратичной формы к нормальному виду с помощью ортогонального преобразования уже не всегда выполнимо.

Лемма. Если квадратичная форма и линейный оператор имеют одну и ту же матрицу относительно какого-нибудь ортонормированного базиса, то они будут иметь одинаковые матрицы и относительно любого другого ортонормированного базиса.

---

Доказательство. Рассмотрим квадратичную форму:

(10)

И линейный оператор, матрица которого относительно какого-либо ортонормированного базиса совпадает с матрицей этой квадратичной формы: .

Этот оператор отображает произвольный вектор на вектор по формулам:

(11)

Тогда квадратичную форму (10) можно записать в виде

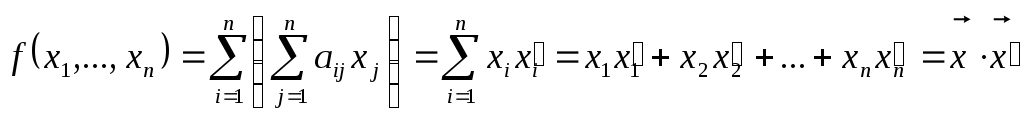(12)

Перейдем к новому ортонормированному базису. Пусть векторы и имеют относительно этого базиса соответственно координаты и , а формулы, связывающие эти координаты, имеют вид

(13)

Выражая скалярное произведение векторов и через их координаты относительно нового базиса, получим с помощью (13)

Отсюда в следствие (12) получаем

(14)

Сравнивая (13) и (14), видим, что данные квадратичная форма и линейный оператор имеют и относительно нового базиса одну и ту же матрицу с элементами .

Теорема. Любая квадратичная форма может быть приведена к каноническому виду с помощью ортогонального преобразования переменных.

Доказательство. Пусть (10)  данная квадратичная форма. Рассмотрим линейный оператор, имеющий относительно некоторого ортонормированного базиса

---