Файл: Основная часть. 4 I. Квадратичные формы..doc

ту же симметрическую матрицу, что и эта квадратичная форма. Характеристическое уравнение этого оператора:

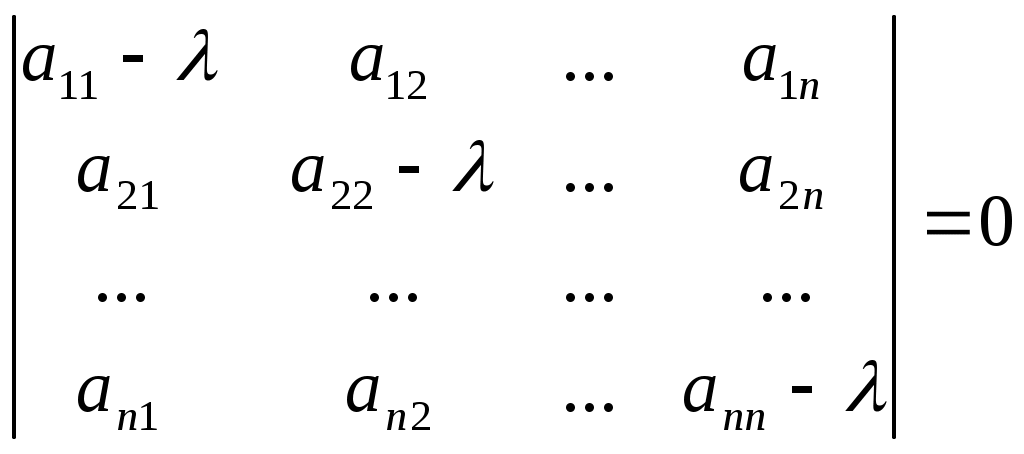(15)

Так как матрица линейного оператора всегда может быть приведена к диагональному виду с помощью соответствующего выбора базиса, то существует ортонормированный базис , относительно которого матрица данного линейного оператора имеет диагональный вид; при этом диагональными элементами будут служить корни характеристического уравнения (15). По лемме квадратичная форма (10) будет иметь в новом базисе ту же матрицу, что и этот линейный оператор, т.е. окажется приведенной к каноническому виду

(16)

здесь каждый корень характеристического уравнения взят столько раз, какова его кратность.

Векторы нового базиса выражаются через векторы старого базиса формулами вида

, (17)

при этом матрица перехода является ортогональной. Таким образом, матрица преобразования

, (18)

приводящего квадратичную форму к каноническому виду, получается при транспонировании этой ортогональной матрицы и, следовательно, также является ортогональной. Теорема доказана.
Способ приведения квадратичной формы к каноническому. Для нахождения коэффициентов в каноническом виде (16) квадратичной формы (10) достаточно решить характеристическое уравнение (17).

Укажем теперь способ нахождения соответствующего ортонормированного базиса и ортогонального преобразования, приводящего квадратичную форму к каноническому виду.

1) Пусть - корень характеристического уравнения

---

, имеющий кратность 1. подставив этот корень в систему (11), принимающую при 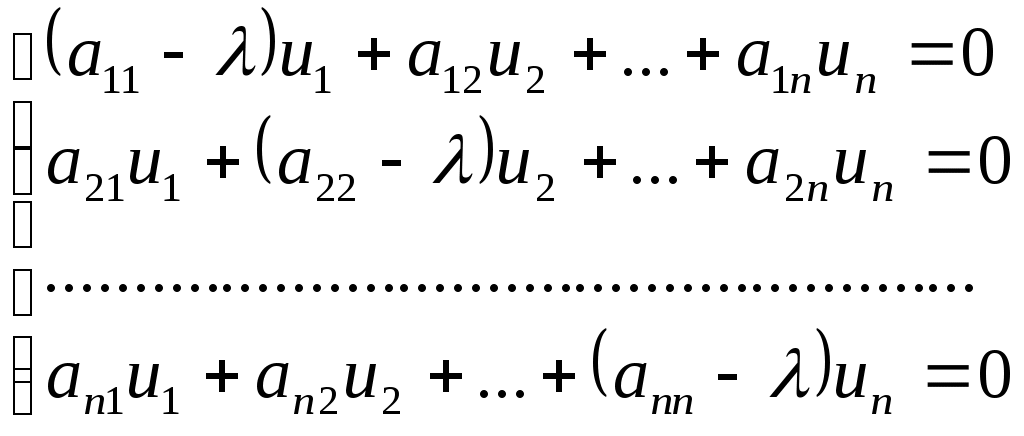вид (19)

Найдем из нее координаты собственного вектора , соответствующего этому собственному значению . Разделив найденный вектор на его длину, получим вектор искомого ортонормированного базиса.

2) Пусть теперь - корень характеристического уравнения, имеющий кратность m>1. после его подстановки в (19) найдем m независимых решений полученной системы, выбрав их так, чтобы они определяли координаты m попарно ортогональных единичных векторов. Эти векторы образуют ортонормированный базис m-мерного подпространства, состоящего из собственных векторов, соответствующих данному собственному значению . Примем найденные векторы за векторы искомого базиса пространства V_n.

Матрицу ортогонального преобразования (18), приводящего квадратичную форму к каноническому виду, можно получить транспонированием матрицы перехода от базиса к базису .

---

II. Квадрики.

1. Определения. Примеры.

Квадрикой(гиперповерхностью второго порядка) в аффинном пространстве A_n называется множество точек, координаты которых в некоторой аффинной системе координат удовлетворяют уравнению второй степени.

В общем виде уравнение квадрики может быть записано следующим образом (20)
где - сумма членов второй степени, т.е. некоторая квадратичная форма , - сумма членов первой степени (так называемая линейная форма): , а – свободный член.

Пример 1. В A₂ квадрика имеет уравнение вида



И является кривой 2-го порядка.

Пример 2. В A₃ квадрика – поверхность 2-го порядка:


Понятие квадрики не зависит от выбора системы координат.

Может случиться, что над полем действительных чисел R для некоторого уравнения (20) нет ни одной удовлетворяющей ему точки. Всё-таки про такое уравнение говорят, что оно есть уравнение квадрики. Иногда при этом гиперповерхность называют мнимой(или нулевой).

Например, говорят, что уравнение задаёт мнимую сферу(в евклидовом пространстве с системой декартовых прямоугольных координат ).

Теорема. Если множество точек в некоторой аффинной системе координат определяется уравнением второй степени, то оно будет определяться уравнением второй степени и в любой другой аффинной системе координат.

Доказательство. Если множество точек задано в старой системе координат уравнением (20), то для получения уравнения данного множества в новой системе достаточно подставить в это уравнение выражения старых координат

---

через новые координаты . При этом не могут получиться члены степени выше второй, т.е. степень уравнения не может повыситься.

Степень уравнения не может и понизиться. Действительно, если бы степень нового уравнения оказалась ниже второй, то при обратном переходе от этого уравнения к уравнению (20) степень уравнения стала бы равной двум, т.е. повысилась; но выше уже было доказано, что это невозможно.

2. Приведение уравнения квадрики к нормальному виду.

Пусть квадрика задана в некоторой аффинной системе координат уравнением (20). Поставим себе цель – упростить это уравнение путем надлежащего выбора новой аффинной системы координат.

Теорема. При соответствующем выборе аффинной системы координат уравнение любой квадрики может быть приведено к одному из следующих видов

(21)

где ,

(22)

где , и

(23)

где , коэффициенты всюду равны +1 или 1.

Доказательство. Вначале произведем линейное преобразование

, приводящее к каноническому виду квадратичную форму .

С геометрической точки зрения это означает переход к новой аффинной системе координат с прежним началом. При соответствующей нумерации новых координат уравнение (20) квадрики примет вид

, где и коэффициенты р₁,…, р_m не равны нулю.

Выделяя полные квадраты, будем иметь

---

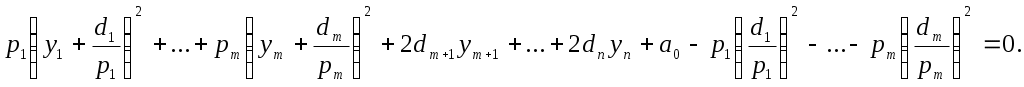Подвергнем систему координат параллельному переносу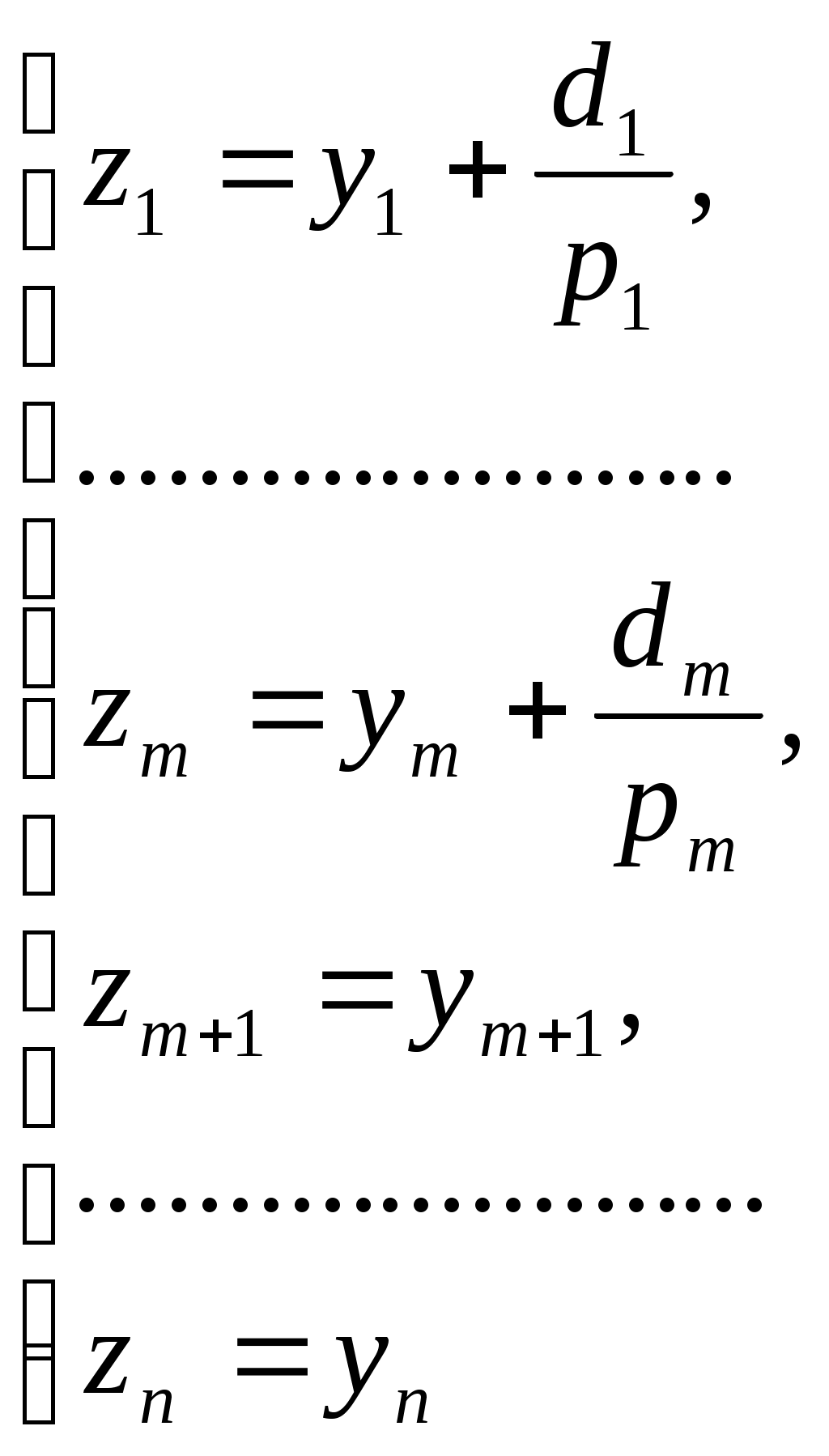



Если ввести обозначение



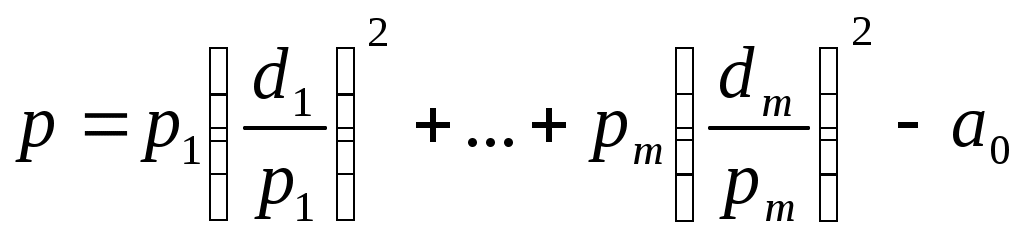
то относительно полученной системы координат квадрика будет иметь уравнение (24)
Заметим, что при m=n формулы параллельного переноса принимают вид

,

а уравнение (24) – вид

Продолжим упрощение уравнения квадрики.

Возможны следующие случаи:

1) Если в уравнении (24) и , то оно имеет вид



Перейдя к новой системе координат по формулам



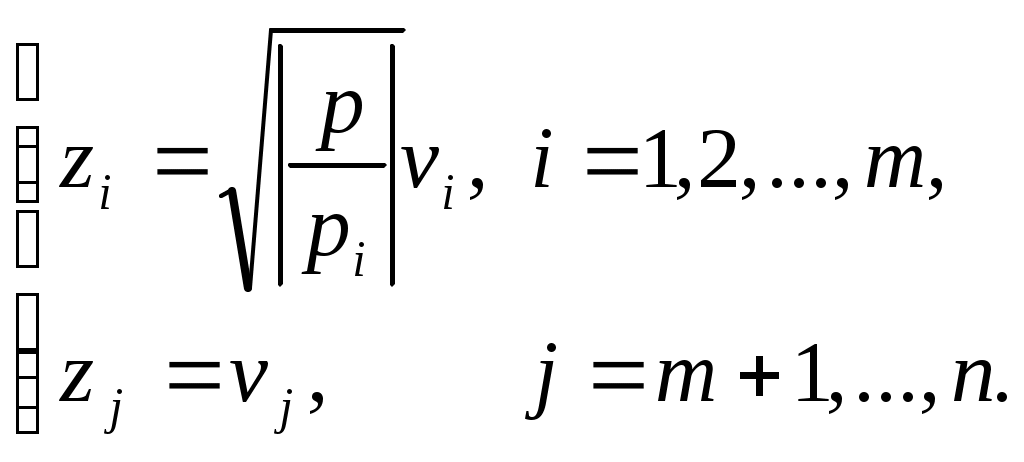
Приведем уравнение квадрики к виду

,

где при и при ;

2) если и , то уравнение (24) имеет вид



После преобразования координат по формулам



будем иметь

,

где при

---