ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 37
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
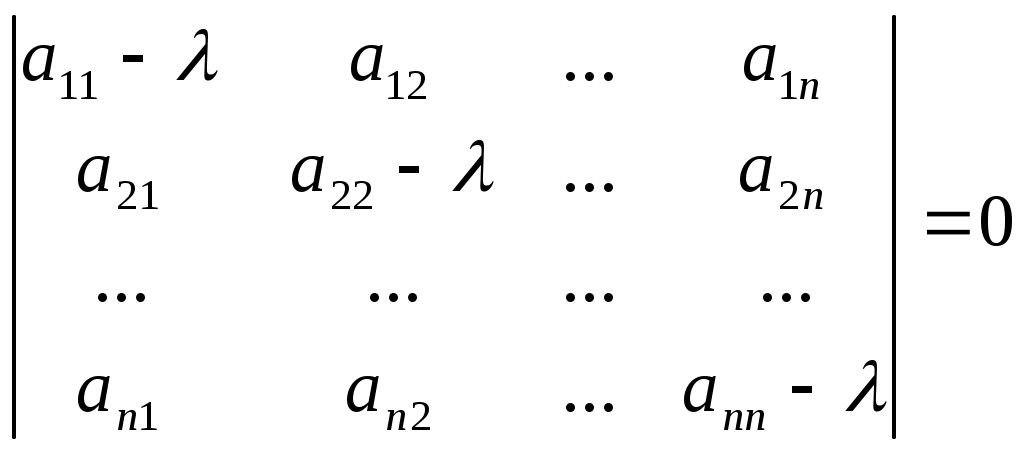 (15)
(15)Так как матрица линейного оператора всегда может быть приведена к диагональному виду с помощью соответствующего выбора базиса, то существует ортонормированный базис
здесь каждый корень характеристического уравнения взят столько раз, какова его кратность.
Векторы нового базиса выражаются через векторы старого базиса формулами вида
при этом матрица перехода является ортогональной. Таким образом, матрица преобразования
приводящего квадратичную форму к каноническому виду, получается при транспонировании этой ортогональной матрицы и, следовательно, также является ортогональной. Теорема доказана.
Способ приведения квадратичной формы к каноническому. Для нахождения коэффициентов
Укажем теперь способ нахождения соответствующего ортонормированного базиса
1) Пусть
, имеющий кратность 1. подставив этот корень в систему (11), принимающую при
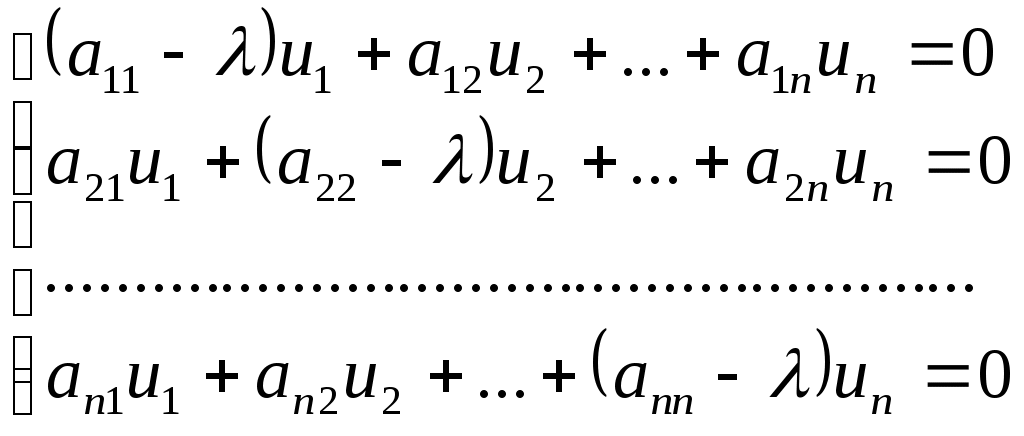 (19)
(19)Найдем из нее координаты собственного вектора
2) Пусть теперь
Матрицу ортогонального преобразования (18), приводящего квадратичную форму к каноническому виду, можно получить транспонированием матрицы перехода от базиса
II. Квадрики.
1. Определения. Примеры.
Квадрикой(гиперповерхностью второго порядка) в аффинном пространстве An называется множество точек, координаты которых в некоторой аффинной системе координат удовлетворяют уравнению второй степени.
В общем виде уравнение квадрики может быть записано следующим образом
где
Пример 1. В A2 квадрика имеет уравнение вида
И является кривой 2-го порядка.
Пример 2. В A3 квадрика – поверхность 2-го порядка:
Понятие квадрики не зависит от выбора системы координат.
Может случиться, что над полем действительных чисел R для некоторого уравнения (20) нет ни одной удовлетворяющей ему точки. Всё-таки про такое уравнение говорят, что оно есть уравнение квадрики. Иногда при этом гиперповерхность называют мнимой(или нулевой).
Например, говорят, что уравнение
Теорема. Если множество точек в некоторой аффинной системе координат определяется уравнением второй степени, то оно будет определяться уравнением второй степени и в любой другой аффинной системе координат.
Доказательство. Если множество точек задано в старой системе координат уравнением (20), то для получения уравнения данного множества в новой системе достаточно подставить в это уравнение выражения старых координат
Степень уравнения не может и понизиться. Действительно, если бы степень нового уравнения оказалась ниже второй, то при обратном переходе от этого уравнения к уравнению (20) степень уравнения стала бы равной двум, т.е. повысилась; но выше уже было доказано, что это невозможно.
2. Приведение уравнения квадрики к нормальному виду.
Пусть квадрика задана в некоторой аффинной системе координат уравнением (20). Поставим себе цель – упростить это уравнение путем надлежащего выбора новой аффинной системы координат.
Теорема. При соответствующем выборе аффинной системы координат уравнение любой квадрики может быть приведено к одному из следующих видов
где
где
где
Доказательство. Вначале произведем линейное преобразование
С геометрической точки зрения это означает переход к новой аффинной системе координат с прежним началом. При соответствующей нумерации новых координат уравнение (20) квадрики примет вид
Выделяя полные квадраты, будем иметь
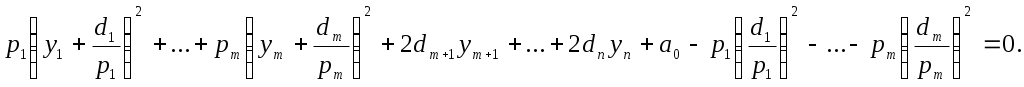 Подвергнем систему координат параллельному переносу
Подвергнем систему координат параллельному переносу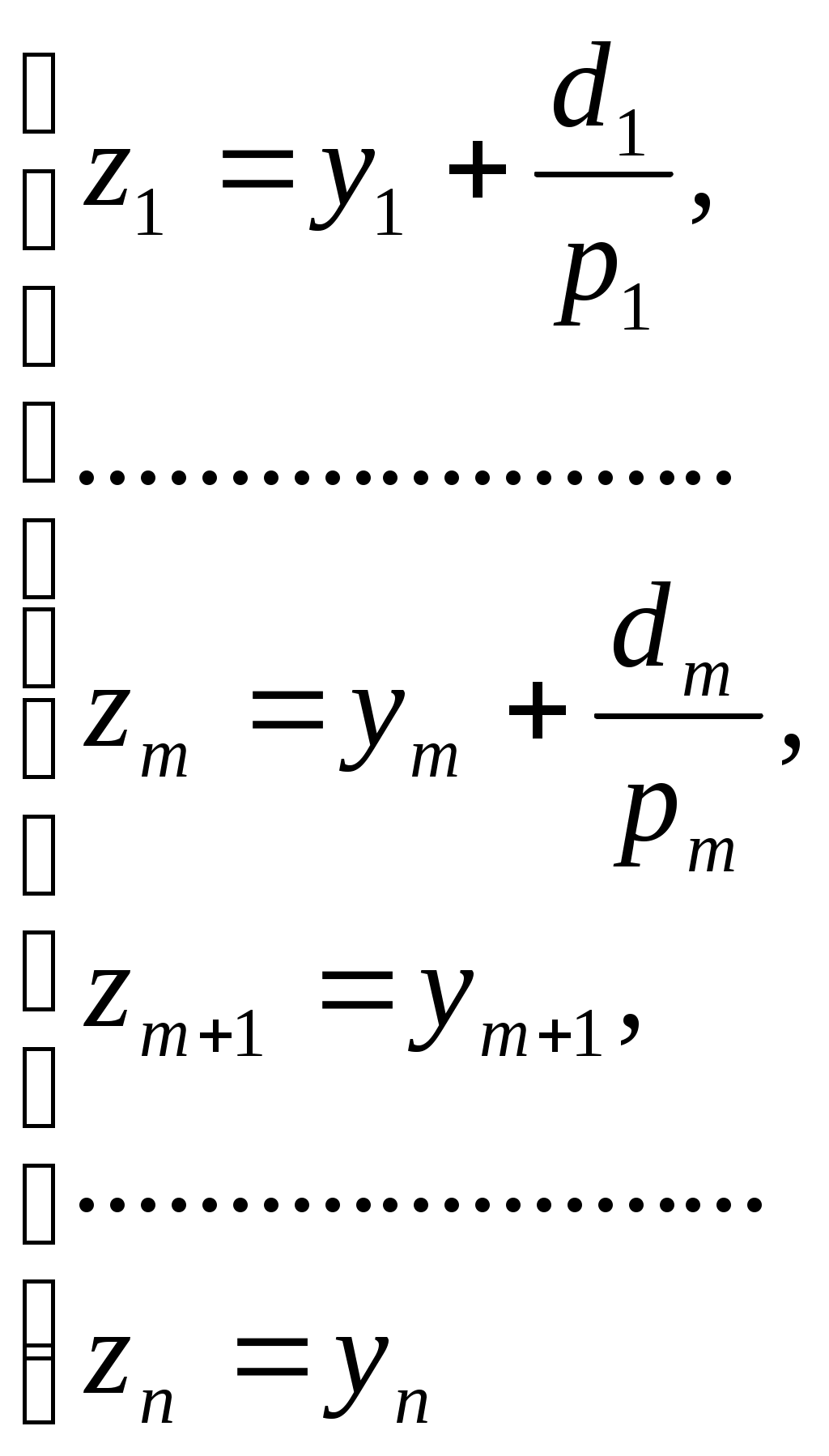
Если ввести обозначение
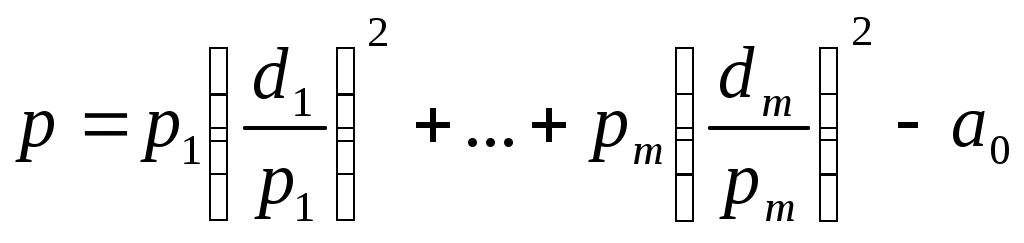
то относительно полученной системы координат квадрика будет иметь уравнение
Заметим, что при m=n формулы параллельного переноса принимают вид
а уравнение (24) – вид
Продолжим упрощение уравнения квадрики.
Возможны следующие случаи:
1) Если в уравнении (24)
Перейдя к новой системе координат по формулам
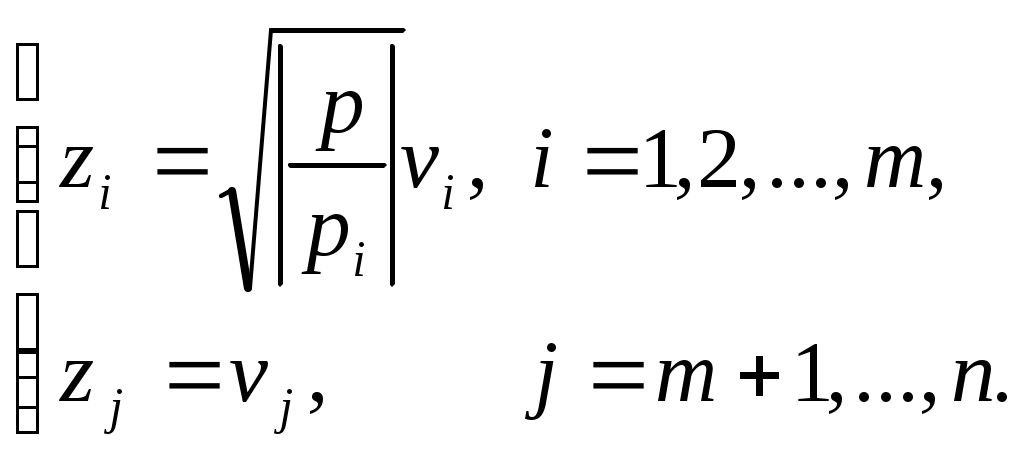
Приведем уравнение квадрики к виду
где
2) если
После преобразования координат по формулам
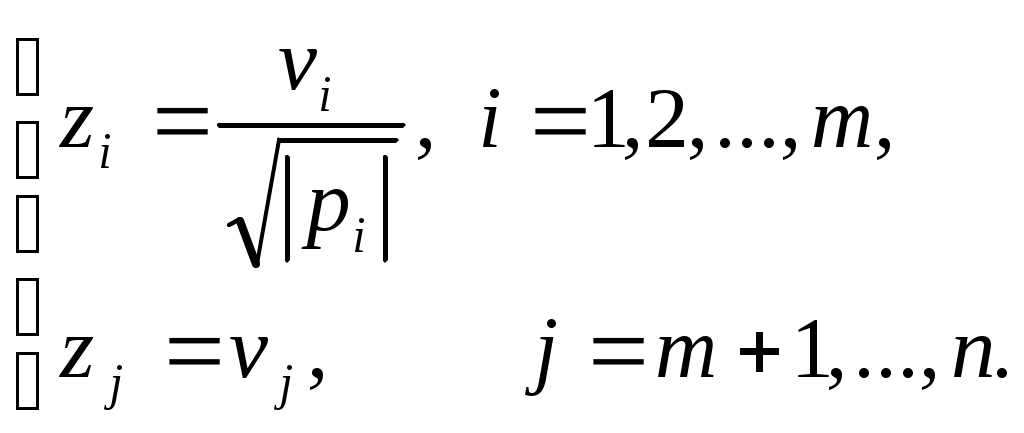
будем иметь
где

