ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.03.2024
Просмотров: 74
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Система решена, она имеет единственное решение:
x1 = 15; x2 = 10; x3 = 13.
Таким образом, решив систему уравнений, мы нашли, что первый банк выплачивает 15% годовых, второй банк — 10% годовых, а третий банк — 13%.
Цит. по: Математика [Электронный ресурс]: учебный курс /
Г.А. Питерцева. — Электронный курс. — М: МИЭМП, 2007. —
Режим доступа к курсу: http://e-college.ru. — П. 6.11.
2.1. Методом обратной матрицы решить систему уравнений:
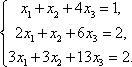
Решение. Обозначим:
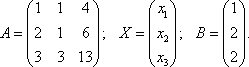
Тогда в матричной форме система имеет вид: АХ = В. Определитель матрицы
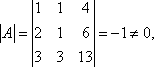т.е. обратная матрица А –1 существует :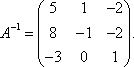
Теперь по формуле X = A-1 B:
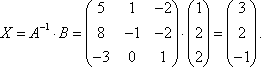
Ответ :(3; 2; – 1).
Цит. по: Высшая математика для экономистов:
Практикум для студентов вузов,
обучающихся по экономическим специальностям /
[Н.Ш. Кремер и др]; под ред. проф.Н.Ш. Кремера. —
2-е изд., перераб. и доп. — М.: ЮНИТИ-ДАНА, 2007. —
(Серия «Золотой фонд российских учебников») — С. 35.
Точнее данная теорема является частным случаем теоремы Лапласа.
Аналитическая геометрия
Тема 1. Прямая на плоскости
Пример 1
Найдите уравнение прямой, проходящей через точку пересечения прямых 3x – 2y = 0 и 5x + y = 0 и точку M1 (5; 17).
План решения
1. Найти точку пересечения прямых, которую обозначим M2, для этого требуется решить систему уравнений
2. Использовать уравнение прямой, проходящей через две точки M1 (x1 ; y1) и M2 (x2 ; y2):
.3. Привести полученное уравнение к общему виду
Ax + By + C = 0, воспользовавшись свойством пропорции (
).| Решение | Комментарий |
| Решим систему уравнений 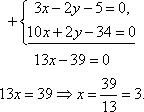   Подставим найденное значение х = 3 в одно из уравнений, например, в первое уравнение: 9 - 2у - 5 = 0, 2y = 4, y = 2. Таким образом, M2 (3; 2) ‑ точка пересечения прямых. Составим уравнение прямой, проходящей через две точки: 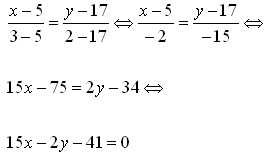 . | Целесообразно использовать метод алгебраического сложения. Для этого уравнять коэффициенты перед одной из переменных, а затем сложить уравнения. Можно обе части разделить на 2, тогда уравнение примет вид: x + y – 1 = 0. |
Пример 3
Найдите координаты точки пересечения прямых 4x + 5y – 9 = 0 и –3x + 2y + 1 = 0.
План решения
1. Решить систему уравнений
Решение
Решим систему уравнений методом алгебраического сложения (можно методом подстановки).
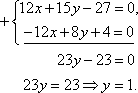
Подставим y = 1 в первое (второе) уравнение системы. Получим 4x + 5 × 1 – 9 = 0, 4x – 4 = 0, x = 1. Точка пересечения имеет координаты (1; 1).
Пример 5
Даны вершины ΔABC , A (1; 2), B (–3; 3), C (5; 0). Найдите уравнение высоты треугольника, опущенной из вершины
A .
План решения
1. Найти координаты вектора
2. Высота, опущенная из вершины A, это прямая, проходящая через точку A и перпендикулярно стороне BC. Поэтому воспользоваться уравнением прямой, проходящей через точку и перпендикулярно вектору:
A (x – x0 ) + B (y – y0) = 0.
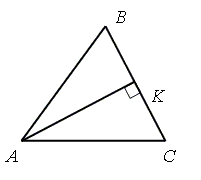
3. В это уравнение вместо x0, y0 подставить координаты точки A , вместо A и B подставить координаты вектора
4. Привести уравнение к виду Ax + By + C = 0.
Решение
Подставим координаты точки и вектора в уравнение прямой A (x – x0) + B (y – y0) = 0:
8(x – 1) – 3(y – 2) = 0,
8x – 8 – 3y + 6 = 0,
8x – 3y – 2 = 0.
Пример 7
Найдите уравнение прямой, проходящей через точки M1 (–4; 3) и M2 (5; –2).
План решения
1. Использовать уравнение прямой, проходящей через две точки M1 (x1 ; y1) и M2 (x2 ; y2):
2. В это уравнение вместо x1, y1 подставить координаты точки M1, а вместо x2, y2 подставить координаты точки M2 .
3. Пользуясь свойством пропорции, привести полученное уравнение к виду Ax + By + C = 0.
Решение
, 
.Подставим координаты этих точек в уравнение прямой:
,
,–5(x + 4) = 9(y – 3),
–5x – 20 – 9y + 27 = 0,
–5x – 9y + 7 = 0.
Пример 9
Найдите угол между прямыми y = 5x + 7 и 3x + 2y – 1 = 0.
План решения
1. Привести уравнения прямых к виду l 1 : k1x + b1 и l 2 : k2x + b2 и определить угловые коэффициенты прямых k1 и k2 .
2. Воспользоваться формулой для нахождения угла φ между прямыми l1 и l2:
.Решение
l 1 : y = 5x + 7, k = 5.
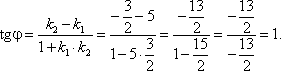
Следовательно, φ = 45°.
Замечание
Если tg φ < 0, то φ — тупой угол.
Пример 11
Уравнение 4x – 3y + 24 = 0 преобразовать к уравнению «в отрезках».
План решения
Уравнение «в отрезках» имеет вид
.1. Перенести свободный член вправо и разделить обе части уравнения на него.
2. Все коэффициенты и знаки убрать в знаменатели дробей.
Решение
4x – 3y + 24 = 0,
,
.Пример 13
Определите уравнение прямой, отсекающей на оси Oy отрезок b = 3 и составляющей с осью Ox угол φ = 60°.
План решения
1. Воспользоваться уравнением прямой с угловым коэффициентом: y = kx + b , где k = tg φ, φ — угол между прямой и осью Ox , b — отрезок, отсекаемый прямой на оси Oy .
Решение
y = kx + b ,
b = 3.
Пример 15
Стороны AB , BC , AC треугольника ABC заданы соответственно уравнениями 8x + 3y + 1 = 0, 2х + у - 1 = 0, 3x + 2y + 3 = 0. Определить координаты вершин треугольника.
План решения
Вершины ΔABC — это точки пересечения соответствующих сторон.
1. Решить три системы уравнений, беря попарно уравнения сторон ΔABC .
Решение
| Решение | Комментарий |
| AB: 8x + 3y + 1 = 0, BC: 2x + y – 1 = 0, AC: 3x + 2y + 3 = 0. 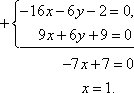  8 × 1 + 3y + 1 = 0, 3y = –9, y = –3. Таким образом, A (1; –3). 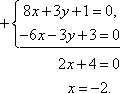  8 × (–2) + 3y + 1 = 0, 3y = 15, y = 5. Таким образом, B (–2; 5). 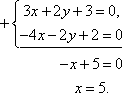  2 × 5 + y – 1 = 0, y = –9. Таким образом, C (5; –9). В итоге: A (1; –3), B (–2; 5), C (5; –9). | Вершина A образована пересечением сторон AB и AC, поэтому решим систему уравнений, составленную из уравнений этих сторон. Систему решаем методом алгебраического сложения. Уравниваем коэффициенты перед y . Найденное значение x подставим в первое (или второе) уравнение. Все остальные системы решаем аналогично. Вершина B образована пересечением сторон AB и BC, поэтому решим систему уравнений, составленную из уравнений этих сторон. Подставим x = –2 в первое уравнение. Вершина C образована пересечением сторон AC и BC, поэтому решим систему уравнений, составленную из уравнений этих сторон. Подставим x = 5 во второе уравнение системы. |
Пример 17