Файл: Дипломды Жмыc мaмaнды 5В010900 Мaтeмaтикa.docx

Тықырып: (5 сынып) Нақты сандар

1-тапсырма. Екі натурал санды қос: 159+65; 204 + 1021. Нәтижесі қандай сан?

2-тапсырма. Екі натурал санды көбейт: 29 * 9, 204*1000. Нәтижесі қандай сан?

3-тапсырма. Екі натурал санды шегер: 191 – 15, 99 – 13, 189-189. Нәтижесі қандай сан?

4-тапсырма. Келесі сандар қандай сандар жиыны болады: (6,7,8,9),(-1,-25), ( 4,3,2,1,0,-1)?

5-тапсырма. Екі бүтін санды бөл: 90:3, 150:10, 20:8. Нәтижесі қандай сан?

Рационал санның анықтамасы: екі бүтін санның бөліндісі (қатынасы) түрінде жазылатын сан.

6-тапсырма. Иррационал сан ол – рационал сан емес деп аударылатыны белгілі болса, иррационал санның анықтамасын бер.

7-тапсырма. Кез келген шеңбердің ұзындығы мен диаметрінің қатынасы ( 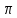)- иррационал сан екені белгілі. Онда шеңбердің ұзындығы мен диаметрі қандай сан болуы мүмкін?

8-тапсырма. 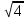саны иррационал және берілген квадраттың ауданы 4 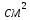екені белгілі болса, квадраттың (шаршының) қабырғасы қандай сан болуы мүмкін?

9-тапсырма. Рационал сан дегеніміз – бөлшек сан деген рас па?

Күтілетін жауаптар:

1. Натурал сан

2. Натурал сан

3. Әрқашан натурал сан емес. Кейде теріс сан, кейде ноль болуы мүмкін

4. Натурал сандар, теріс сандар, бүтін сандар

5. Кейде бөлшек сан шығады.

6. Анықтама: Иррационал сан деп екі бүтін сандардың бөліндісі түрінде жаза алмайтын санды айтады.

7. «Кез келген шеңбердің ұзындығы мен диаметрі бір уақытта бүтін сан бола алмайды». «Кез келген шеңбердің ұзындығы мен диаметрі бір уақытта рационал сан да бола алмайды».

8. «Берілген квадраттың қабырғасы бүтін сан бола алмайды», «берілген квадраттың қабырғасы рационал сан да бола алмайды». Себебі: екі рационал санның көбейтіндісі (аудан көбейтіндісі арқылы есептегенде) иррационал болса, онда ол рационал сандардың біреуі иррационал сан мен екінші рационал санның бөліндісі болар еді, ал ол рационал санның анықтамасына қайшы.

9. Жалған, мысалы : 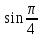( 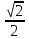бөлшек, бірақ рационал сан емес).

---

2.4 Қызықты материал. Жұмыс дәптері

Танымдық қызығушылықты қалыптастыру құралдарының бірі-ұқыптылық. Қызықты ойын, барлық ерекше, күтпеген жағдайлар балаларда таңдану сезімін, таным процесіне қызығушылық тудырады, оларға кез-келген оқу материалын игеруге көмектеседі.

Математика сабағында ойын барысында оқушылар әртүрлі жаттығуларды орындайды, онда жиынтықтарды салыстыруға, арифметикалық амалдарды орындауға, ауызша есепте жаттығуға, есептерді шешуге тура келеді. Ойын оқушыны іздеу жағдайына қояды, жеңіске деген қызығушылықты оятады, демек, тез, жиналған, епті, тапқыр болуға, тапсырмаларды нақты орындауға, ойын ережелерін сақтауға үйретеді.

Ойындарда, әсіресе ұжымдық, тұлғаның адамгершілік қасиеттері қалыптасады. Сабақтарда сіз келесі ойындарды пайдалана аласыз: «БАСПАЛДАҚ», «ҰШҚЫР ОЙ», «КІМ ЖЫЛДАМ», «ДЕСАНТШЫЛАР", "ЖАЛҒАСТЫРЫҢЫЗ, АШУЛАНБАҢЫЗ", "ДӘЛ БАҒЫТТА", "ПОЙЫЗ", "ДОП КІМГЕ БЕРІЛЕДі" және тағы басқалар.

Мен мектепте ойындарды ұйымдастыруға белгілі бір талаптар қоямын.

• 
  Ойын оқушылардың еркін шығармашылығына және өзіндік іс-әрекетіне негізделуі керек.
  
• 
  Ойын белгілі бір жастағы оқушылар үшін қол жетімді болуы керек, ойынның мақсаты қол жетімді, ал дизайны түрлі – түсті және әр түрлі болуы керек.
  
• 
  Ойынның міндетті элементі-оның эмоционалдылығы.
  
• 
  Ойындарда командалар немесе ойынның жеке қатысушылары арасындағы жарыстың маңызды шарттарының, ережелерінің болуы.
  

Жұмыс дәптері. Квадрат теңдеулер

XX ғасырдың 90-шы жылдарында оқу құралдарының жаңа жанры – жұмыс дәптерлері пайда бола бастады. Жұмыс дәптерлері нақты оқулыққа қосымша ретінде құрастырылады.

Жұмыс дәптерлерін бірнеше типтерге бөлуге болады.

1. Жаттығулар үшін арналған дәптерлер. Оларды басқаша өздік жұмысы дәптерлері дейді.

Тапсырмаларды орындау үшін оқушы теориялық материалды білуі қажет.

2. Графиктік модельдеу принципине негізделген жұмыс дәптерлері. Оның негізін суреттер мен белгілерден құралған тапсырмалар құрайды.

3. Хрестоматия – дәптерлер. Мұнда әртүрлі ақпарат көздерінен мәтіндер, ғылыми және көркем әдебиеттер фрагменттері жинақталады. Бұл типті дәптерлермен жұмыс әлдеқайда көп уақыт қажет ететіндігінен оларды үй жұмысын орындауға қолданған қолайлы .

Құралдардың аталған әрбір типінің өзіндік ерекшеліктері бар. Айталық,

I – ші топ жұмыс дәптерлері оқулық мазмұнын меңгеруге көмектесетін сұрақтар мен тапсырмалардан тұрады. Мұндай дәптер өткен материалды қайталауға ыңғайлы.

---

Жұмыс дәптерлері арқылы әр оқушымен жеке жұмыс істеу жүзеге асырылады, жеке оқушының мүмкіндіктері мен қабілеттері айқындалады.

Танымдық есептерді шығару нәтижесінде алынған білімдер тұрақтылықпен және саналылықпен ерекшеленеді. Бұл жағдайларда оқушылардың жеке танымдық әрекеттері күшейе түседі.

“Жұмыс дәптері” қазіргі практикада кеңінен қолданылып жүрген Ресей оқулығының мазмұнына сәйкес құрастырылған. Оқулық мазмұны 5 тараудан тұрып, III-тарау “Квадрат теңдеулер” деп аталады. Тарау үш параграфқа бөлінген: “Квадрат теңдеулер және оның түбірлері”, “Квадрат теңдеудің түбірлерінің формуласы” және “Бөлшек рационал теңдеулер”. Жұмыс дәптерінде есептер де осы тақырыптарға сай құралған.

Дәптердің мазмұны, негізінен, стандарт емес есептер мен тапсырмалардан тұрады. Әр тапсырманың соңында есеп шешімін жазу үшін орын қалдырылған. Қиындығы деңгейі жағынан есептер “орташадан жоғары” деуге болады. Есептердің оқушылар үшін қиын болуы біріншіден, олардың шешімдері қазақтың тұрмысы мен мәдениетіне, шаруашылық жүргізу ерекшеліктеріне тағы басқа жайларға қатысты мәліметтер, деректер, атауларды білуді қажет етеді; екіншіден, есептер көбінесе оқушы үшін үйреншіксіз тілде баяндалып, есеп мәтінінен математика тіліне көшу, кейін математикалық есеп шығарылған соң, жалпы жауапты тұжырымдау да оқушы үшін бірталай қиындықтар туғызады.

Бұл есептерді оқулық бойынша тақырыпқа сәйкес практикалық есептермен қосып немесе оқулықтағы негізгі есептер шығарылғаннан кейін, игерілген білімді “мектеп қабырғасынан тыс” жағдайларда іске асыру мақсатында қолдануға болады.

“Квадрат теңдеулер және оның түбірлері” тақырыбына дәптерде екі тапсырма келтірілген.

­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­Есеп мазмұны: Еркін күнделігінде апта күндерінде қарап отырып:

-Дүйсенбі мен сейсенбінің “көбейтіндісі” жұмаға тең болса, дүйсенбі айдың нешінші жұлдызы? – деп сұрады досы Ермектен.

Бұған Ермек:

- Білмеймін, менің білетінім бұл айдың отызыншы жұлдызы-менің туған күнім, дүйсенбіге келеді,- деп жауап қайтарады.

Екеуінің де есептері дұрыс болуы мүмкін бе?

Түсініктеме. Дүйсенбі мен сейсенбінің көбейтіндісін былай түсіну керек: мысалы, дүйсенбі 5-і болса, онда сейсенбі 6-сы және жұма 30-ы (6·5) болуы керек.

Есеп шешімін табу үшін апта күндерін белгісіз айнымалы арқылы белгілеп алайық, айталық, дүйсенбі айдың х-ші жұлдызы болса, сейсенбі (х+1)-і, сәрсенбі (х+2)-сі т.б. Сонда есеп шартының математикалық моделі болып келесі теңдеу саналады:

---

Х(Х+1)=X+4

Бұған Ермектің айтқанын қоссақ, x=30 болуы керек. Әрине, “таза алгебралық” теңдеудің шешімі x=30 емес, расында, 30·31≠30+4. Алайда квадрат теңдеуді шешіп, жауап талдауын жасайтын болсақ, Ермектің айтқаны Еркіндікіне қайшы болмайтынын көреміз: x²+x=x+4, бұдан x=2, яғни дүйсенбі екісіне келеді, олай болса, айдың 9-шы, 16, 23, 30-шы жұлдыздары да дүйсенбіге келеді.

Есепті басқаша да шығарып көруге болады. Айталық, екеуі де дұрыс сөйлеген болсын, сонда 30-ы дүйсенбі, олай болса 23-і, 16, 9, 2-де дүйсенбіге келеді. Сонымен қатар, x(x+1)=x+4 теңдеуін x=2 мәні қанағаттандырады. Ендеше болжам дұрыс.

Есептің мақсаты – стандарт емес сұрақтарға жауап беру үшін, өзіндегі математикалық аппаратты мүмкіндігінше қолдана білу, есептегі математикалық талапты, “проблеманың математикасын” тани білуге оқушыны баулу.

Келесі тапсырмада “жеті күннің басқа атауын қолданып, жоғарыдағы есепті тұжырымда” делінген, яғни оқушыға құрастырылған теңдеу бойынша, жеті күннің басқаша атауын пайдаланып, есеп мазмұнын құрастыру керек. Ол үшін айталық, бүгін х-і болсын, сонда ертең (х+1)-і, бүрсігүні (х+2)-і т.т. болады.

Олай болса, x(x+1)=x+4 – теңдеуін “қазақ тіліне” аударсақ, “бүгін мен ертеңгі күн көбейтіндісі ауыр күнге тең” деген тұжырым аламыз.

Егер “Х” – бүгін емес “бүрсігүні” болса, онда бүрсігүні мен арғы күн көбейтіндісі азынаға “тең” болар еді т.б. Ескеретін жай, жеті күннің басқаша атауы үшін Ермектің тұжырымы орынсыз.

Квадрат теңдеулерді екі мүшенің квадратын айыру тәсілімен шешуге дәптерде төрт есеп келтірілген.

Бірінші есеп. “Шапқыншылардың барлаушыларын байқап қалған қарауыл басшысының: “олардың бір қылышына біздің төрт қылыш қарсы, тірідей ұстайық бұларды”, - деген сөзін есепсіз жүре алмайтын сарбаздардың бірі: “жаудың қолы дәл соншаға еселенгеннің өзінде бізде үш қол артық” деп қостады. Күштерді бағала...”.

Математика тіліне көшу үшін “олардың қылыш санын” х десек, бізде –(4*Х) қылыш болуы керек. “Жаудың қолы дәл соншаға еселенсе” олардың саны (Х*Х), сонымен қатар, бұл сан (4*Х)-тен үшке кем. Ендеше келесі квадрат теңдеу бұл есептің моделі болып табылады: х²=4x-3

Бұл теңдеу дискрименант арқылы да, Виет теоремасы көмегімен де, толық квадратты бөлу арқылы да жеңіл шығарылады, яғни есепті басқа тақырыптармен байланыстырып қолдануға болады.

Теңдеудің екі шешімі бар: 1 және 3, яғни жауап: барлаушылар-үшеу, ал қарауылда 12 адам, немесе бір барлаушы және 4 қарауыл.

---

Есеп мақсаты: x²-4x+3=0 түріндегі стандарт, ”сұр” математикалық теңдеуге әдеби-көркем бейне, қалып беру арқылы оқушылардың пәнге қызығушылығын жандандыру, оқушыға математика тіліне қазақ тілінен және керісінше өту ережелерін білетін “тілмаш” ролін жүктеу.

Екінші есеп. Керітайдың есебі: Менің қалтамдағы ақша “а” кг алмаға жетсе, “-а²+4а-5” кг алмаға жетеді ме?

Есептің негізгі идеясы (-а²+4а-5) өрнегінің мәндері жиынын бағалау, ол үшін екі мүшенің квадратын айыра білу керек:

-a²+4a-5=-(a²-4a+5)=-(a²-4a+4+1)=-((a-2)²+1).

Жақшаның ішінде оң сандардың қосындысы тұр, ендеше өрнектің мәні

а-ның кез келген мәні үшін теріс сан болып табылады. Салмақ теріс бола алмауынан“ ақша жетеді немесе жетпейді” деу орынсыз.

Үшінші есеп. “Алдар түсінде қазына тауып алыпты.

-Сандықта көрсетілген алтынның мөлшерінен аз алсаң немесе оны өз қолыңмен көтеріп әкетпесең оянып кетесің,- дейді оған біреу жоғарыдан.

Сандықтағы жазуға қараса онда: “Мөлшері а²-4а+26 пұт, ал “а”-ның орнына қай санды қойғың келсе, мейлің, өзің біл” делінген екен. Алдар біраз ойланып, “менен де қулар бар екен” деп ояна салыпты.

Түсініктеме қажет...”.

Алдыңғы есепте сияқты, квадрат үш мүшеден екі мүшенің квадратын айырып жазатын болсақ, есептегі алгебралық өрнектің мәнін бағалауға болады: a²- 4a + 26 = (a-2)² + 22

Бұл өрнек a=2 болғанда ең кіші мәнге ие болады, ал бұл 22 пұт. Әрине, мұндай салмақты Алдар көтере алмайды...

“Квадрат теңдеулерді пайдаланып есептер шығару” тақырыбына үш есеп және бір тапсырма ұсынылған.

Бірінші есеп. Бүгінгі күн мен ертеңгі күн көбейтіндісі ауыр күн мен соңғы күн көбейтіндісінің үштен бір бөлігіне тең болса, арғы күн нешесі болғаны? Бұл есеп шешімі дәптердегі ең бірінші есепке ұқсас, квадрат теңдеу шешіміне келтіріледі:



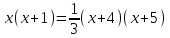
Теңдеудің оң түбірі x=5, мұндағы х-ол бүгінгі күн, онда арғы күн (х+3), яғни 8-і.

Екінші есеп. “Жасын сұраған құрдасына Қожа:

–Балам екеуміздің жасымыздың көбейтіндісі айырымынан 36 есе көп, сонымен қатар, ұлым туған жылы мен екінші мүшелімді тойлағанмын,- дейді.

Сұрақ қойып есепті шығар”.

Қожаның сөзін талқылайтын болсақ, бірқатар қорытындылар жасауға болады. Ол қорытындыларды есеп сұрағының жауабы ретінді қарастырсақ, сұрақ қою қиын емес. Сонымен, х - баланың жасы болсын, сонда екінші мүшел 25 жас екенін ескерсек, Қожа баласынан 25 жасқа үлкен екендігі шығады, яғни ол (х+25) жаста.

---