Добавлен: 20.03.2024
Просмотров: 64
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.4 Қызықты материал. Жұмыс дәптері
3. МАТЕМАТИКАНЫ ОҚЫТУДАҒЫ ТАПСЫРМАЛАРДЫҢ МОТИВАЦИЯЛЫҚ ФУНКЦИЯСЫ
3.1 Зейінді дамытуға бағытталған тапсырмалар
3.2 Қабылдау мен қиялды дамытуға бағытталған тапсырмалар
3.3 Логикалық ойлауды дамытуға бағытталған тапсырмалар
Жастарының көбейтіндісі х(х+25) өрнегіне, ал айырымы ((х+25)-х) өрнегіне сәйкес, сонымен қатар, алдыңғы өрнек мәні соңғысынан 36 есе көп екенін ескерсек, келесідей теңдеу аламыз:
х2+25х=36*25
Теңдеудің оң түбірі x=20, яғни баласы жиырмада, ендеше өзі қырық бесте.
Келесі тапсырмада “жеті күн” атауларын қолданып, бірінші есепке ұқсас есеп құрастыру керек. Оқушы үшін бұл шығармашылық жұмыс болып табылады. Есепті дұрыс құрастыра алған бала квадрат теңдеулердің қолданбалық мүмкіншіліктерін түсініп, оқушы өзін құрастырылған есептің авторы ретінде сезінуінің психологиялық мәні жоқ емес. Бұл – оқушының білімге құлшынуының себебі де бола алады.
Үшінші есеп. “Дихан атайдың шөбересі мен шөпшегінің жастарының көбейтіндісі баласының жасының онындай. Аталардың әрқайсысы алдынғысынан 20 жасқа кіші екені белгілі болса, Дихан атайдың немересі нешеде?”.
Есепті шығару үшін жеті атаның атауы мен орналасу тәртібін білу керек. Ізделінді белгісізді, яғни немеренің жасын х деп белгілесек (x-20)(x-40)=(x+20)*10 теңдеудің аламыз, мұнда (х-20)- шөбере жасы, (х-40) - шөпшек жасы, (х+20)-баласының жасы.
Квадрат теңдеудің екі түбірі бар x1=10, x2=60. Бірінші түбір нақтылыққа сай емес, ендеше немересі 60 жаста.
Оқулықтағы келесі тақырып - “Виет теоремасы”. Дәптерде бұл тақырып үшін бір есеп және есеп құрауға бір тапсырма берілген.
Есеп: “Берілген теңдеулердің қайсыларының шешімі болып, бала мен боз баланың жастары алынуы мүмкін?
Жауапты негізде:
-
x2-25x+6=0 -
x2+10x-50=0 -
2x2-40x+150=0
4. 3x2-30x-24=0 “.
Виет теоремасы бойынша, бала мен боз бала жастарының қосындысы кері алынған екінші коэффициентке, ал көбейтіндісі бос мүшеге тең болуы керек (жоғарғы коэффициенті a=1 жағдайында). 2-ші және 4-ші теңдеулердегі бос мүшелер теріс сандар, сондықтан оларды қарастырмаса да болады. Қалған екеуі үшін Виет теоремасын жазайық:
х1+x2=25 х1+x2=20
х1*x2=6 және x1*x2=75 (2-ге қысқартқанан кейін)
Бірінші жүйедегі х- тердің біреуі (0;1) аралығында, ал бала деп 1 мен 7 жас арасындағыларды айтады. Сондықтан, екінші жүйені қарастыру ғана қалады. Жүйе шешімі x1=5, x2=15. Бұл нақтылыққа сәйкес: яғни бала-бесте, боз бала -он бесте.
Келесі тапсырма: “Қазақта он жасқа келген балаға қозы бағуды сеніп тапсырып, ол балаларды “қозы жасындағы” деп, дәл солай “он бес пен жиырма бестің арасын “қой жасы” деп, жиырма бес пен қырықтың арасын “жылқы жасы” деп есептеген.
Осыны қолданып алдыңғы есепке ұқсас есеп құрастырып көр”.
Дәптерде бұл тапсырма үшін оқушыға біржарым бет орын қалдырылған. Ойлаптапқыштық пен шығармашылықты талап ететін бұл тапсырманың үйге берілгені дұрыс.
Тараудың соңғы бөлігі бұл - “Бөлшек рационал теңдеулер”. Бөлшек – рационал теңдеулерді шешу амалдары игерілгеннен кейін, оларды қолдануға оқулықта мәселе есептер қарастырылады. Олар, негізінен, “Қозғалыс есептері” және “бірігіп жұмыс істеуге” есептер. Дәптердегі осы тақырыпқа сәйкес құрастырылған бірінші есеп “қозғалыс есебі” болып саналады.
Есеп: “Жайлау мен қыстау арасы екі көш жер (30 шақырым). Көштен бір сағатқа кеш шыққан Бекдауыл ауылдастарын қуып жетпек болады. Сағатына көштің бір сағатта өтетін жолынан жарты шақырымға артық жол жүріп отырып, кешке түнекке Бекдауыл олармен бірге жетеді.
Сұрақ қойып, есепті шығар. Есеп шешімі квадрат теңдеуге келтірілмесе, сұрақты басқаша қой”.
Қозғалыс есептері, әдетте, жол, жылдамдық, уақыт шамаларының біреуіне қатысты құралған теңдеу арқылы шешіледі. Біздің есепте көш пен
Бекдауылдың уақыттарының айырымы белгілі, сондықтан уақытқа қатысты теңдеу құрудың орны бар: tk=t0+1, мұнда tk – көш уақыты, t0 – Бекдауылдың уақыты. Жүрілген жолдары тең, -15 шақырым (бір көш жер), - сондықтан жылдамдықтарды анықтайық. Есеп шартынан, егер көш жылдамдығы х км/сағ болса, Бекдауылдың жылдамдығы (х+1/2)км/сағ болатыны шығады.
Ендеше,
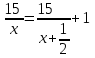
Теңдеудің оң түбірі х=2.5, бұдан көш жылдамдығы 2.5 км/сағ., ал Бекдауыл жылдамдығы 3км/сағ. Ізделінді белгісіз ретінде, мысалы, көштің жылдамдығын сұрауға болады.
2.5 Геометриялық материал
Танымдық қызығушылықтардың дамуына геометрикалық материалды қолдану ықпал етеді.
1. Геометриялық фигуралардан тұратын суреті бар плакат ілу.
Сұрауға болады:
Күннің суреті қандай фигуралардан тұрады?
Дене қандай фигурамен ұсынылған?
Осы фигураның ауданын, оның жақтарының ұзындықтарын өлше және тап
2. Балаларға геометриялық фигураларды таратып, тапсырма беріңіз-осы фигуралардан үй, шырша, қайық және т. б. жасаңыз.
Тапсырма:
Логикалық кестеде жетіспейтін фигураны анықтаңыз

16-сызба.
Тапсырма:
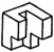
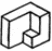
| Төменде берілген суреттерде қай екі фигураларды бір-біріне жалғағанда кубты құрайтынын табыңыз. | ||||||||
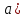 |  | 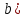 |  | 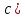 |  | 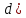 | 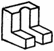 | |
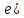 |  | 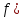 | 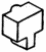 | 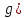 |  | 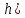 |  | |
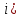 | 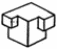 | 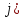 |  | 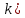 |  | 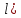 |  | |
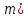 |  | 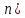 | 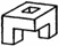 | 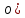 |  | 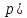 | 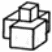 | |
17- сызба
3. МАТЕМАТИКАНЫ ОҚЫТУДАҒЫ ТАПСЫРМАЛАРДЫҢ МОТИВАЦИЯЛЫҚ ФУНКЦИЯСЫ
Математиканы оқытудағы міндеттердің рөлі өте зор. Олар оқытудың көптеген нақты мақсаттарына қызмет ете алады, әртүрлі дидактикалық функцияларды орындай алады. Оқу процесінде міндеттердің оқу функциясын кеңінен қолдану оны белсендіру құралдарының бірі болып табылады. Тапсырмаларды мұндай қолдану оқушылардың бағдарламалық материалды саналы түрде қабылдауына, берік білімді игеруге, оқушылардың ақыл-ой белсенділігін дамытуға ықпал етеді.
Математиканы оқыту әдістемесіндегі ең маңызды проблема - оқу процесін жетілдіру жолдарын іздеу және оқушылардың танымдық іс-әрекетіндегі белсенділікті дамыту. Бұл мәселені шешу үшін математиканы оқытуда қолданбалы және практикалық бағытты жүзеге асыру әдістерін жетілдіру қажет. Математиканы мұғалімнің жұмысына тапсырмалар арқылы оқыту арқылы енгізу арқылы бұл мәселені шешуге болады. Математиканы оқытуда есептер өте маңызды рөл атқарады. Олар нақты оқу мақсаттарына қызмет ете алады және әртүрлі дидактикалық функцияларды орындай алады. Білім беру процесін белсендіру үшін тапсырмалардың мотивациялық функциялары кең қолданылады. Бұл оқушылардың бағдарламалық материалды саналы қабылдауына, берік білімді игеруіне және ақыл-ой әрекетін дамытуға көмектеседі.
Тапсырмалардың мотивациялық функциясын қолдану кезінде келесі дидактикалық мақсаттарға қол жеткізіледі:
-
Нақты теориялық материалды оқып үйренудің қажеттілігі мен пайдалылығын негіздеу; -
Жаңа ұғымдарды енгізуге дайындық; -
Абстрактілі теорияның белгілі модельдерімен танысу; -
Нақты анықтамалар мен ұғымдардың орындылығын дәлелдеу; -
Белгілі математикалық объектілердің кез-келген қасиеттерін ашу; -
Оқыған жаңа теорияның байланысын орнату; -
Күрделі мәлімдемелерді дәлелдеуге дайындық; -
Белгілі бір есептерді шешудің жаңа әдістерімен таныстыру; -
Бір мәселені шешудің әр түрлі әдістерінің тиімділігін салыстыру.
Практикалық мазмұны бар тапсырмалар жаңа математикалық материалды оқуды ынталандыру үшін де ерекше маңызға ие. Жаңа математикалық білім мен әдістердің қажеттілігін есептердің осы түрін шешу қажеттілігімен негіздеу өте заңды. Математикалық теорияны білу және түсіну қажеттілігіне баса назар аудара отырып, практикалық іс-әрекет қажеттіліктерінің әсерінен оқушылар ғылыми көзқарастарын қалыптастырады.
