Добавлен: 20.03.2024
Просмотров: 77
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.4 Қызықты материал. Жұмыс дәптері
3. МАТЕМАТИКАНЫ ОҚЫТУДАҒЫ ТАПСЫРМАЛАРДЫҢ МОТИВАЦИЯЛЫҚ ФУНКЦИЯСЫ
3.1 Зейінді дамытуға бағытталған тапсырмалар
3.2 Қабылдау мен қиялды дамытуға бағытталған тапсырмалар
3.3 Логикалық ойлауды дамытуға бағытталған тапсырмалар
Математикалық теорияны есептер құрастыру арқылы ілгерілету мұғалімге проблемалық оқыту элементтерін сабақта қолдануға қолайлы жағдайлар жасайды. Математиканы оқытудың білімдік, дамытушылық, тәрбиелік және практикалық мақсаттарына жету үшін проблемалық сипаттағы мәселелердің құндылығын асыра бағалау мүмкін емес. Бұл тапсырмалар бағдарламалық материалды оқып үйренудің пайдалылығын негіздей отырып, жаңа ұғымдар мен әдістерді енгізу құралы бола алады. Осы тапсырмаларды қолдану кезінде математикалық теорияны жақсы меңгеру қамтамасыз етіледі, мектеп оқушылары тапсырмаларды, іздеу, зерттеу және дәлелдеу әдістерін, негізгі ақыл-ой операцияларын өз бетінше орындауға үйренеді, математикалық объектілердің маңызды қасиеттерін бөліп көрсетеді, пәнге деген қызығушылықты қалыптастырады. Проблемалық оқыту элементтерін қолдану студенттерді ойлануға итермелейтін ортада орналастырады, олар үйренгендерін автоматты түрде қолдана алатын, сонымен қатар өздері үшін жаңалық ашатын болады.
Оқушыларды жаңа математикалық теорияны игеруге дайындауға арналған тапсырмаларды олардың тұжырымдалуы жаңа білім мен дағдыларды игеру қажеттілігіне ғана емес, сонымен қатар кейіннен алынған білімдерді басқа мәселелердің кең тобын шешу үшін пайдалануға әкелетін етіп таңдау керек.
Сөздік есептер, жаттығулар, практикалық тапсырмалар, зертханалық жұмыс, «жаңа теорияны ашу» жағдайында оқушыны бірқатар жағдайда қоюға бағытталған, расталатын немесе жоққа шығарылатын гипотезалар ұсынуға бағытталған тапсырма-сұрақтарды, дәлелдемелерді қолданған жөн.
Жаңа математикалық теорияны игеруге түрткі болу үшін тапсырмаларды қолданудың нақты мысалдарын қарастырайық.
№1.Оқушылардың ондық бөлшектерді көбейту тақырыбын зерттеуде келесі тапсырмаларды қою арқылы қорытындылауға болады.
Тапсырма 1.1. Бір кг алманың бағасы - 240 теңге. 7 кг алманың құнын табыңыз.
Бұл мәселенің шешімі бастауыш сынып оқушыларына түсінікті: 240 * 7 = 1680 (тг).
Оқушыларға тағы бір сұрақ қояйық: 7 кг алманың құнын қалай табуға болады, егер бір кг алманың бағасы 240,6 тг болса? Нәтижесінде біз жаңа тапсырма аламыз.
Тапсырма 1.2. Бір кг алманың бағасы 240,6 теңгені құрайды. 7 кг алманың құнын табыңыз.
Есепті шешкен кезде оқушылар бұл есептің шешілуі алдыңғы есепке ұқсас екендігін байқайды, 240,6 * 7 = 1684,2 (тг).
Әрі қарай, сандық мәліметтерді өзгерту арқылы мұғалім жаңа есеп шығарады.
Тапсырма 1.3. Бір кг алманың бағасы 240,6 теңгені құрайды. 4,8 кг алманың мәнін табыңыз.
1.1 және 1.2 есептерін шешумен ұқсастығы бойынша оқушылар алманың құны 240,6 * 4,8 (теңге) болады деген қорытындыға келеді. Бірақ оқушыларға бұл есептің сандық шешімін табу қиын болады, өйткені олар ондық бөлшектерді көбейту ережесімен әлі таныс емес. Демек, мұндай есептерді шешу жаңа математикалық теорияны игеру қажеттілігін тудырады. Мұғалім ондық бөлшектерді көбейту ережесін түсіндіреді, содан кейін есеп шығаруға оралады және оқушылармен бірге нәтиже алады: 240,6 * 4,8 = 1154,88 (теңге).
№2.Келесі зертханалық жұмыс арқылы мұғалім оқушыларды тік бұрышты үшбұрыштың сүйір бұрыштарының қосындысын табуға жетелей алады.
Зертханалық жұмыс. Оқушылар сызғыш пен транспортирді қолдана отырып, қадамдарды дәйекті түрде орындауы керек: үш тікбұрышты тұрғызу, бұрыштардың градустық өлшемдерін өлшеу, олардың нәтижелерін кестеге енгізу. Әрі қарай, кестелік деректерді талдап, бұрыштардың қосындысы неге тең екендігі туралы қорытынды жасауы керек.
№3. Тапсырманың толықтығын талдау үшін проблемалық сипаттағы тапсырмалар-сұрақтарды қолдануға болады.
Тапсырма. Бір кездері екі егіз ағайынды болған, олардың біреуі күн сайын тәуліктің үштен бір бөлігін ұйықтаған. Олар 72 жасқа дейін осылай өмір сүрді. Осы уақыт аралығында ағайындылардың әрқайсысы қанша жыл ұйықтады?
Балаларды проблеманы талдауға жетелеу керек, олар: «Екінші ағасы неше сағат ұйықтады?», «Мәселенің негізгі сұрағына жауап беруге бола ма?» деген сұрақтар туралы ойлануы керек. Содан кейін қорытынды жасаймыз: бұл тапсырмалар толық емес. Екінші ағайынның күніне қанша сағат ұйықтағанын білмейміз. Сондықтан біз есептің негізгі сұрағына жауап бере алмаймыз.
Тапсырма. Суреттегі учаскенің ауданын есептеу формуласын құрастыр.


18-сызба.
Шешімі. Учаскенің ауданы S = 62*a - 143*17.
Қысқаша айтқанда, оқыту кезінде тапсырмалардың мотивациялық функциясын кеңінен қолдану - оқушылардың математикалық дайындығының сапасын және олардың интеллект деңгейін жоғарылатудың тиімді құралы болып табылады.
3.1 Зейінді дамытуға бағытталған тапсырмалар
Танымдық қызығушылықты үнемі күшейту, оларды дамыту үшін оқушының өзіндік өсу сезімін, санасын тудыратын құралдарды қолдану қажет.
Жауап жоспарын жасаңыз, досыңызға сұрақ қойыңыз, жауапты талдап, оны бағалаңыз, айтылғанды қорытындылаңыз, мәселені шешудің басқа әдісін іздеңіз – осы және басқа да көптеген әдістер оқушыны өз іс-әрекетін түсінуге итермелейді, тұрақты танымдық қызығушылықтың қалыптасуына әкеледі.
Тапсырма:
Қандай да бір заңдылықпен берілген тізбекті жалғастырыңыз
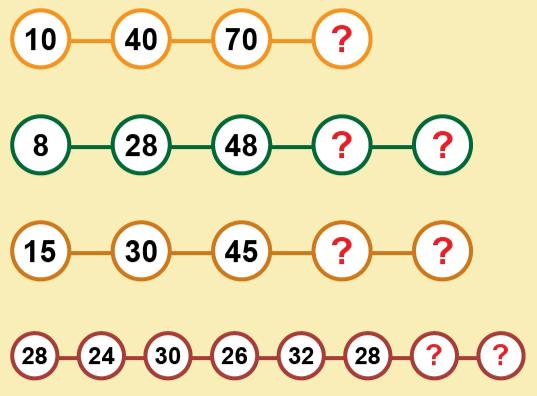
19-сызба
Тапсырма:
Нөмірленген алты фигураның қайсысы бос орынды алу керек?
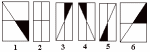
20-сызба
Тапсырма:
Жасырылған санды табыңыз:
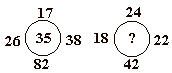
21-сызба.
Оқушының оқу іс-әрекеті процесінде танымдық процестердің даму деңгейі үлкен рөл атқарады: назар, қабылдау, байқау, қиял, есте сақтау, ойлау. Танымдық процестерді дамыту және жетілдіру осы бағыттағы мақсатты жұмыс кезінде тиімдірек болады, бұл балалардың танымдық мүмкіндіктерін кеңейтуге әкеледі.
Тапсырма:
Суреттердің әрқайсысында қанша үшбұрыш бейнеленген?









22-сызба

23-сызба
3.2 Қабылдау мен қиялды дамытуға бағытталған тапсырмалар
Қабылдау-бұл шындықты, оның объектілері мен құбылыстарын сезім мүшелеріне тікелей әсер ету кезінде қабылдаудың танымдық процесі. Бұл ересек адамның да, баланың да ойлау мен практикалық іс-әрекетінің, адамның қоршаған әлемге, қоғамға бағдарлануының негізі. Байқауды қабылдау мен тәрбиелеуді ұйымдастырудың тиімді әдістерінің бірі-салыстыру. Бұл жағдайда қабылдау тереңірек болады.
Ойын және оқу әрекеттері нәтижесінде қабылдаудың өзі дербес әрекетке, бақылауға айналады. Ол үшін мен келесіні қолданамын







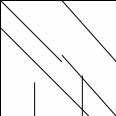
24-сызба
-
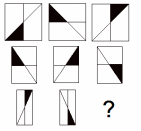
Қандай фигура жетіспейді
 |  |  |
 | |  |
 |  |  |
25-сызба
-
Қандай фигуралар жетіспейді.
 |  |  |
| |  | |
 |  | |
 | |  |
 |  |  |
 |  | |
26-сызба
