Файл: Методические рекомендации по выполнению и защите курсовых работ (проектов) по дисциплине социальная психология.docx
Добавлен: 12.04.2024
Просмотров: 57
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вторичные методы непосредственно проверяют, доказывают или опровергают гипотезы, поставленные в ходе исследования.
Показатели исследования – измеряемые признаки внешних действий испытуемых, их высказываний и скрытых физиологических реакций.
Варианты – числа представляющие собой результаты измерений (единичные показатели).
Вариационный ряд – все замеры, расположенные в один ряд в порядке возрастания или убывания.
Медианой называется значение изучаемого признака, который делит выборку, упорядоченную по величине данного признака пополам.
Модойназывают количественное значение исследуемого признака, наиболее часто встречающееся в выборке.
Интерваломназывается группа, упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением [9; С. 120-122].
Среднеарифметическое значение представляет собой среднюю оценку, изучаемого в эксперименте психологического качества вычисляется во всех случаях, когда произведено интегральное измерение, и находится путем суммирования всех результатов и делением получившейся суммы на число членов вариационного ряда
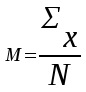
Если произведено N измерений, то полученные единичные показатели обозначаются как Х1, Х2, Х3………Хn
М – средняя арифметическая;
- знак суммирования
Для измерения вариации оценок внутри группы пользуются другими характеристиками вариационного ряда – дисперсией и средним квадратическим отклонением [7; С. 23].
Дисперсия, как статистическая величина характеризует насколько частые значения отклоняются от средней величины в одной выборке. Определяется дисперсия как средний как средний квадрат отклонения варианты от ее среднего арифметического значения и обозначается буквой 2.
Для вычисления дисперсии, от каждой из вариант Х, вычитают значение средней арифметической М. Получают ряд величин отклонений:
d = X – M
Теперь нужно найти среднее отклонение от средней арифметической М. По сумме всех отклонений d равна нулю, т.к. одни отклонения от М положительны, а другие отрицательны. Поэтому суммируют не отклонения d, а их квадраты. Полученную сумму делят на число вариант N, в результате чего получают величину 2, которая называется дисперсией.
2 =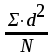
Квадратный корень из дисперсии и есть интересующее нас среднее отклонение от М:
= 
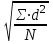
Эта величина (сигма) называется средним квадратическим отклонением. Теперь зная величины М и , мы имеем полную статистическую характеристику совокупности вариант Х1, Х2, Х3………Хn
Значение М и достаточно и для сравнения между собой двух средних арифметических. Мы можем определить имеется ли между М1 и М2существенное (статистически значимое) различие или нет.
Для определения статистической достоверности разницы М1 и М2 пользуются критериемСтьюдента t.
t =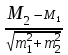
, где m1 m2 представляют собой величины средних ошибок, которые вычисляются по формуле:
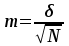
Величина t дает возможность определить не только достоверность различия средних М1 и М2, но и определить уровень достоверности. Для этого существуют специальные таблицы определения уровня значимости.В таблице представлены величины t для трех уровней достоверности: пятипроцентного (Р = 0,05), однопроцентного (Р = 0,01), однопромилльного (Р = 0,001) [7; С. 23-25].
Критерий Стьюдента - t дает нам возможность поэлементного анализа сложноорганизованных объектов действительности. Исходя из результатов исследований в школе В.В.Белоуса, поэлементная и интегральная характеристики не совпадают. Для интегрального анализа нам необходимо вычислить линейный дискриминатор. Его суть заключается в следующем. Если между попарно взятыми показателями разных объектов отсутствует линейная корреляция, то ее можно обнаружить не частным, а комплексным способом, т.е. путем сопоставления системы показателей друг с другом. С математической точки зрения такой интегральный показатель может быть установлен на основе
дискриминантного анализа. С этой целью широко используется формула, предложенная О.М.Калининым:
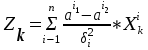, где
а1 - среднеарифметическое (i-того) отдельного показателя 1-ой группы;
а2 - среднеарифметическое (i-того) отдельного показателя 2-ой группы;
i - среднеквадратическое отклонение по совокупности i-ых показателей в 1 и 2 группах;
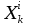- абсолютное выражение каждого испытуемого по каждому показателю;
i - 1,2,3,…n (n- число показателей);
k - номер испытуемого;
- суммирование по всем нормированным показателям.
Статистическое сравнение по комплексным показателям тоже осуществляется с помощью t-критерия Стьюдента.
Говоря о преимуществах линейного дискриминатора по сравнению с поэлементным сравнением, мы, тем не менее, должны признать, что линейная дискриминантная функция не в состоянии дать конкретное и детализированное представление о характере зависимостей свойств рассматриваемой психической реальности. Такого рода информация может быть получена из результатов корреляционного анализа.
Чтобы исследовать меру статистической взаимосвязи между показателями вычисляется коэффициент корреляции (критические значения выборочного коэффициента линейной корреляции).
Корреляционный анализ.
Для практического психолога или психодиагноста очень важно владеть оперативными статистическими методами обработки экспериментальных данных, не требующими машинной обработки. К таким практическим методам относится ранговый коэффициент корреляции, который поможет психологам и педагогам определить статистическую связь, зависимость между экспериментальными и "жизненными" показателями, подтвердить прогностическую силу данного теста.
Определение взаимосвязи показателей, измененных в шкале порядка, производят с использованием ранговых коэффициентов корреляции.
М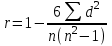
ы познакомимся с одним из них - ранговым коэффициентом корреляции Спирмена (обозначается буквой r). Его вычисляют по формуле:
где:
d = x1 - y1 - разность рангов данной пары показателей;
х - место, занятое в математической олимпиаде;
у - число месяцев занятий в математической школе конкретного ученика.
Все прочие условия (класс, возраст, пол и др.) примерно одинаковы. Результаты наблюдений и опроса представлены в таблице 3 (столбцы 1 и 2).
Так как показатели изменены в шкале порядка, вычислим значение рангового коэффициента корреляции.
Запишем алгоритм вычисления рангового коэффициента корреляции Спирмена (r) по шагам.
Шаг 1. Проранжировать (упорядочить и приписать порядковые номера) показатели х и у. Так как х уже упорядочен и обозначает соответствующие ранги, перепишем его значения в столбец 3. Показателю у приписываем ранги следующим образом: значению 10 – ранг 1; 9 – ранг (2+3)/2= 2,5; 8-ранг 4, и т.д.
Таблица 3
Расчет рангового коэффициента корреляции Спирмена
Шаг 2. Вычислить разность рангов d = (xl-yl) (столбец 5);
Шаг 3. Вычислить квадрат разности d2= (xl-yl)2 (столбец 6);
Шаг 4. Вычислить сумму квадратов разности d2 = 25,5 Шаг 5. Вычислите значение r
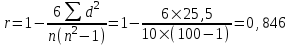
Значение r = 0,846 характеризует сильную положительную взаимосвязь. Другими словами, опыт, накопленный в математической школе, достаточно сильно определяет успешность выступления на математической олимпиаде, при прочих равных условиях.
Ранговый коэффициент корреляции Спирмена изменяется в пределах от -1 до +1. Достоинством ранговых коэффициентов корреляции является простота вычисления. Поэтому ими следует пользоваться для быстрой оценки взаимосвязи, когда показатели или признаки не могут быть изменены точно, но могут быть ранжированы.
В таблице 4 представлены критические значения коэффициентов корреляции для различных степеней свободы. Заметим, что зависимость коэффициента корреляции зависит и от заданного уровня значимости или принятой вероятности допустимой ошибки в расчетах.
Метод множественных корреляций в отличие от метода парных корреляций позволяет выявить общую структуру корреляционных зависимостей, существующих внутри многомерного экспериментального материала, включающегося более двух переменных, и представить эти корреляционные зависимости в виде некоторой системы.
Таблица 4
Критические значения коэффициентов корреляции для различных степеней свободы
Показатели исследования – измеряемые признаки внешних действий испытуемых, их высказываний и скрытых физиологических реакций.
Варианты – числа представляющие собой результаты измерений (единичные показатели).
Вариационный ряд – все замеры, расположенные в один ряд в порядке возрастания или убывания.
Медианой называется значение изучаемого признака, который делит выборку, упорядоченную по величине данного признака пополам.
Модойназывают количественное значение исследуемого признака, наиболее часто встречающееся в выборке.
Интерваломназывается группа, упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением [9; С. 120-122].
Среднеарифметическое значение представляет собой среднюю оценку, изучаемого в эксперименте психологического качества вычисляется во всех случаях, когда произведено интегральное измерение, и находится путем суммирования всех результатов и делением получившейся суммы на число членов вариационного ряда
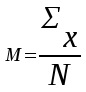
Если произведено N измерений, то полученные единичные показатели обозначаются как Х1, Х2, Х3………Хn
М – средняя арифметическая;
- знак суммирования
Для измерения вариации оценок внутри группы пользуются другими характеристиками вариационного ряда – дисперсией и средним квадратическим отклонением [7; С. 23].
Дисперсия, как статистическая величина характеризует насколько частые значения отклоняются от средней величины в одной выборке. Определяется дисперсия как средний как средний квадрат отклонения варианты от ее среднего арифметического значения и обозначается буквой 2.
Для вычисления дисперсии, от каждой из вариант Х, вычитают значение средней арифметической М. Получают ряд величин отклонений:
d = X – M
Теперь нужно найти среднее отклонение от средней арифметической М. По сумме всех отклонений d равна нулю, т.к. одни отклонения от М положительны, а другие отрицательны. Поэтому суммируют не отклонения d, а их квадраты. Полученную сумму делят на число вариант N, в результате чего получают величину 2, которая называется дисперсией.
2 =
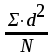
Квадратный корень из дисперсии и есть интересующее нас среднее отклонение от М:
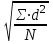
= Эта величина (сигма) называется средним квадратическим отклонением. Теперь зная величины М и , мы имеем полную статистическую характеристику совокупности вариант Х1, Х2, Х3………Хn
Значение М и достаточно и для сравнения между собой двух средних арифметических. Мы можем определить имеется ли между М1 и М2существенное (статистически значимое) различие или нет.
Для определения статистической достоверности разницы М1 и М2 пользуются критериемСтьюдента t.
t =
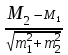, где m1 m2 представляют собой величины средних ошибок, которые вычисляются по формуле: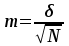 | Число степеней свободы d, f | Уровни значимости, p | ||
| 0,05 | 0,01 | 0,001 | |
| 5 | 2,57 | 4,03 | 6,87 |
| 10 | 2,23 | 3,17 | 4,59 |
| 20 | 2,09 | 2,84 | 3,85 |
| 30 | 2,04 | 2,75 | 3,65 |
| 60 | 2,00 | 2,66 | 3,46 |
Величина t дает возможность определить не только достоверность различия средних М1 и М2, но и определить уровень достоверности. Для этого существуют специальные таблицы определения уровня значимости.В таблице представлены величины t для трех уровней достоверности: пятипроцентного (Р = 0,05), однопроцентного (Р = 0,01), однопромилльного (Р = 0,001) [7; С. 23-25].
Критерий Стьюдента - t дает нам возможность поэлементного анализа сложноорганизованных объектов действительности. Исходя из результатов исследований в школе В.В.Белоуса, поэлементная и интегральная характеристики не совпадают. Для интегрального анализа нам необходимо вычислить линейный дискриминатор. Его суть заключается в следующем. Если между попарно взятыми показателями разных объектов отсутствует линейная корреляция, то ее можно обнаружить не частным, а комплексным способом, т.е. путем сопоставления системы показателей друг с другом. С математической точки зрения такой интегральный показатель может быть установлен на основе
дискриминантного анализа. С этой целью широко используется формула, предложенная О.М.Калининым:
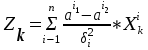, гдеа1 - среднеарифметическое (i-того) отдельного показателя 1-ой группы;
а2 - среднеарифметическое (i-того) отдельного показателя 2-ой группы;
i - среднеквадратическое отклонение по совокупности i-ых показателей в 1 и 2 группах;
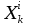- абсолютное выражение каждого испытуемого по каждому показателю;i - 1,2,3,…n (n- число показателей);
k - номер испытуемого;
- суммирование по всем нормированным показателям.
Статистическое сравнение по комплексным показателям тоже осуществляется с помощью t-критерия Стьюдента.
Говоря о преимуществах линейного дискриминатора по сравнению с поэлементным сравнением, мы, тем не менее, должны признать, что линейная дискриминантная функция не в состоянии дать конкретное и детализированное представление о характере зависимостей свойств рассматриваемой психической реальности. Такого рода информация может быть получена из результатов корреляционного анализа.
Чтобы исследовать меру статистической взаимосвязи между показателями вычисляется коэффициент корреляции (критические значения выборочного коэффициента линейной корреляции).
Корреляционный анализ.
Для практического психолога или психодиагноста очень важно владеть оперативными статистическими методами обработки экспериментальных данных, не требующими машинной обработки. К таким практическим методам относится ранговый коэффициент корреляции, который поможет психологам и педагогам определить статистическую связь, зависимость между экспериментальными и "жизненными" показателями, подтвердить прогностическую силу данного теста.
Определение взаимосвязи показателей, измененных в шкале порядка, производят с использованием ранговых коэффициентов корреляции.
М
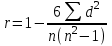ы познакомимся с одним из них - ранговым коэффициентом корреляции Спирмена (обозначается буквой r). Его вычисляют по формуле:где:
d = x1 - y1 - разность рангов данной пары показателей;
х - место, занятое в математической олимпиаде;
у - число месяцев занятий в математической школе конкретного ученика.
Все прочие условия (класс, возраст, пол и др.) примерно одинаковы. Результаты наблюдений и опроса представлены в таблице 3 (столбцы 1 и 2).
Так как показатели изменены в шкале порядка, вычислим значение рангового коэффициента корреляции.
Запишем алгоритм вычисления рангового коэффициента корреляции Спирмена (r) по шагам.
Шаг 1. Проранжировать (упорядочить и приписать порядковые номера) показатели х и у. Так как х уже упорядочен и обозначает соответствующие ранги, перепишем его значения в столбец 3. Показателю у приписываем ранги следующим образом: значению 10 – ранг 1; 9 – ранг (2+3)/2= 2,5; 8-ранг 4, и т.д.
Таблица 3
Расчет рангового коэффициента корреляции Спирмена
| №п/п | 1 | 2 | 3 | 4 | 5 | 6 |
| X | У | X1 | Y1 | X1-Y1 | (X1-Y1)2 | |
| 1. | 1 | 9 | 1 | 2,5 | -1,5 | 2,25 |
| 2. | 2 | 10 | 2 | 1 | 1 | 1 |
| 3. | 3 | 8 | 3 | 4 | -1 | 1 |
| 4. | 4 | 7 | 4 | 5 | -1 | 1 |
| 5. | 5 | 9 | 5 | 2.5 | 2.5 | 6.25 |
| 6. | 6 | 4 | 6 | 75 | -1,5 | 2,25 |
| 7. | 7 | 4 | 7 | 7,5 | -0,5 | 0,25 |
| 8. | 8 | 3 | 8 | 95 | 1.5 | 2,25 |
| 9. | 9 | 5 | 9 | 6 | 3 | 9 |
| 10. | 10 | 3 | 10 | 9,5 | 0,5 | 0,25 |
| Сумма = 25,5 | ||||||
Шаг 2. Вычислить разность рангов d = (xl-yl) (столбец 5);
Шаг 3. Вычислить квадрат разности d2= (xl-yl)2 (столбец 6);
Шаг 4. Вычислить сумму квадратов разности d2 = 25,5 Шаг 5. Вычислите значение r
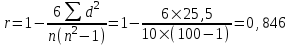
Значение r = 0,846 характеризует сильную положительную взаимосвязь. Другими словами, опыт, накопленный в математической школе, достаточно сильно определяет успешность выступления на математической олимпиаде, при прочих равных условиях.
Ранговый коэффициент корреляции Спирмена изменяется в пределах от -1 до +1. Достоинством ранговых коэффициентов корреляции является простота вычисления. Поэтому ими следует пользоваться для быстрой оценки взаимосвязи, когда показатели или признаки не могут быть изменены точно, но могут быть ранжированы.
В таблице 4 представлены критические значения коэффициентов корреляции для различных степеней свободы. Заметим, что зависимость коэффициента корреляции зависит и от заданного уровня значимости или принятой вероятности допустимой ошибки в расчетах.
Метод множественных корреляций в отличие от метода парных корреляций позволяет выявить общую структуру корреляционных зависимостей, существующих внутри многомерного экспериментального материала, включающегося более двух переменных, и представить эти корреляционные зависимости в виде некоторой системы.
Таблица 4
Критические значения коэффициентов корреляции для различных степеней свободы
| Число степеней свободы | Коэффициент корреляции | ||
| 0,1 | 0,05 | 0,01 | |
| 2 | 0,900 | 0,950 | 0,990 |
| 3 | 0,805 | 0,848 | 0,959 |
| 4 | 0,729 | 0,811 | 0,917 |
| 5 | 0,669 | 0,754 | 0,874 |
| 6 | 0,622 | 0,707 | 0,834 |
| 7 | 0,582 | 0,666 | 0,798 |
| 8 | 0,549 | 0,632 | 0,765 |
| 9 | 0,521 | 0,602- | 0,735 |
| 10 | 0,497 | 0,576 | 0,708 |
| 20 | 0,360 | 0,423 | 0,537 |
| 30 | 0,296 | 0,349 | 0,449 |
| 50 | 0,239 | 0,272 | 0,354 |