Файл: 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 90
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, то решение системы дает единственную точку пересечения прямых.
15. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых.
Общее уравнение прямой и его исследование
Рассмотрим уравнение прямой с угловым коэффициентом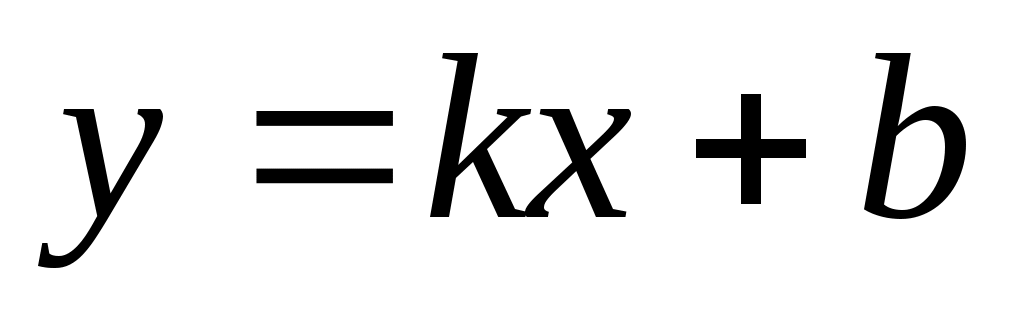 . Перенесем все слагаемые в левую часть и перепишем его в следующем виде:
. Перенесем все слагаемые в левую часть и перепишем его в следующем виде:
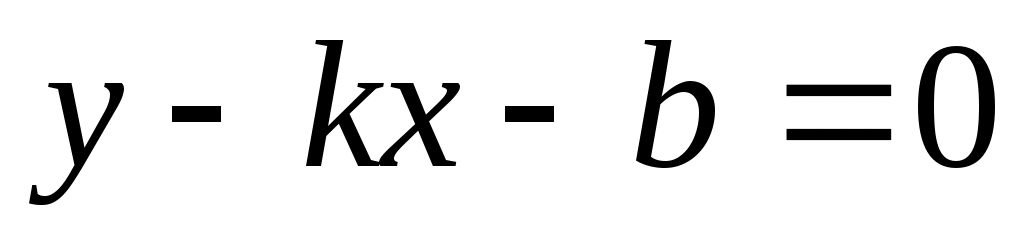 ,
,
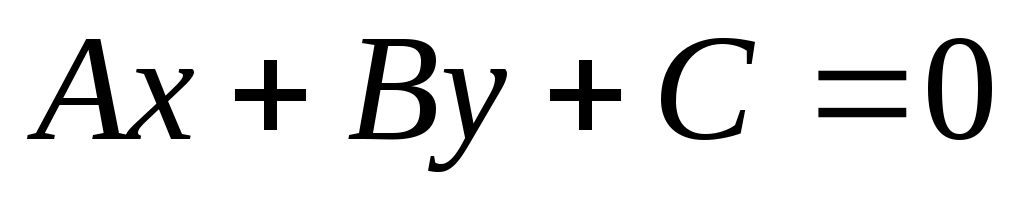 - (3.6)
- (3.6)
общее уравнение прямой, где и не равны нулю одновременно, т.е.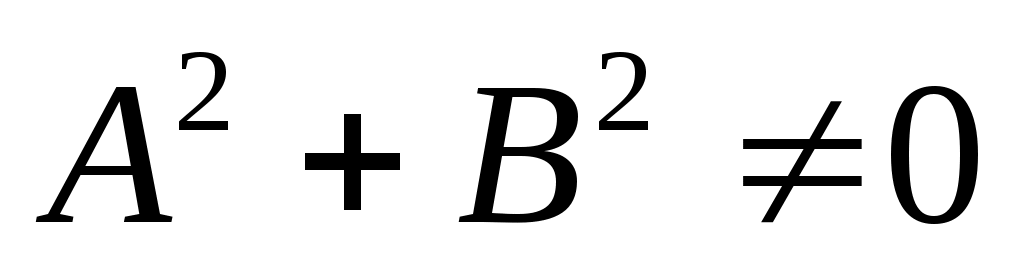 .
.
Рассмотрим частные случаи уравнения (3.6).
Если , , то получим (уравнение прямой с угловым коэффициентом);
Если , , то (уравнение прямой, проходящей через начало координат);
Если , , то (уравнение прямой, параллельной оси Оу);
Если , , то (уравнение оси Ох).
Если , то получим (уравнение прямой, параллельной оси Оу);
Если , то (уравнение оси Оу).
Т.о., при любых значениях коэффициентов , (не равных одновременно нулю) и уравнение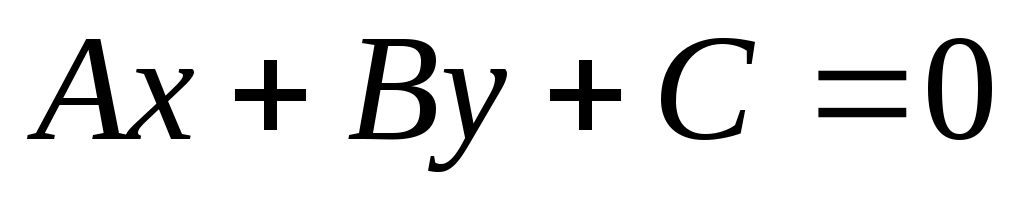 есть уравнение некоторой прямой линии на плоскости Оху.
есть уравнение некоторой прямой линии на плоскости Оху.
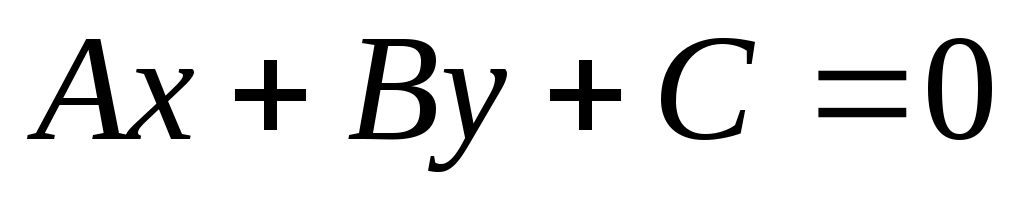 - общее уравнение прямой.
- общее уравнение прямой.
Условия параллельности и перпендикулярности двух прямых:
Если прямые и параллельны, то угол и , откуда из формулы угла между двумя прямыми
. И наоборот, если , то по этой же формуле и .
Т.о., равенство угловых коэффициентов является необходимым и достаточным условием параллельности 2х прямых.
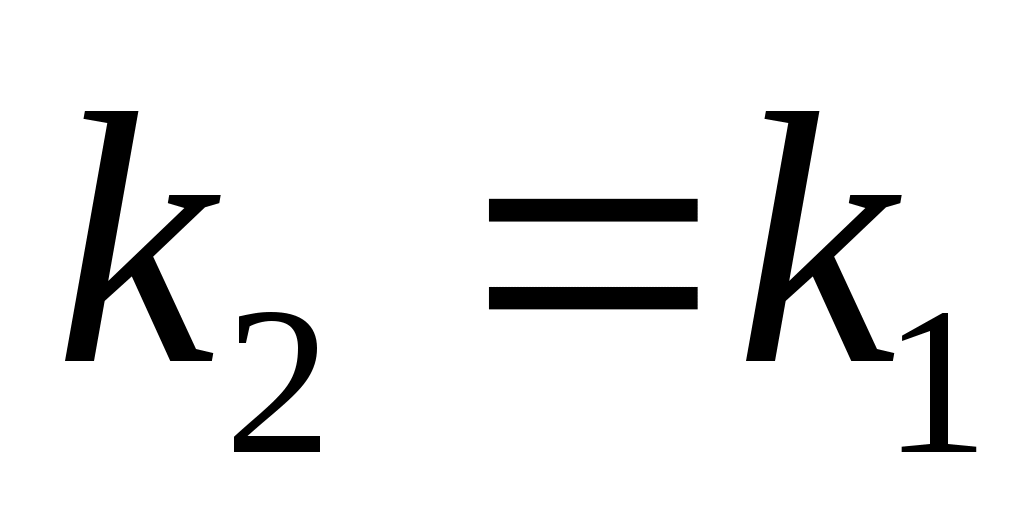 - условие параллельности двух прямых.
- условие параллельности двух прямых.
Если прямые перпендикулярны, то , при этом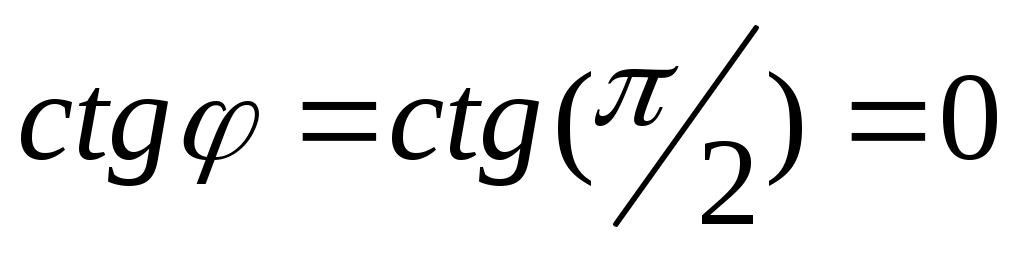 или
или 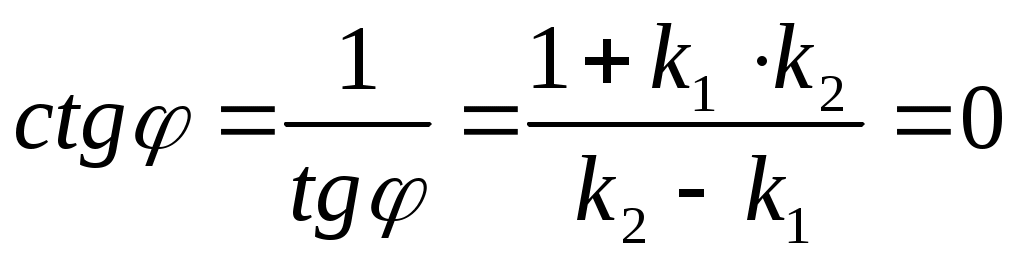 , откуда
, откуда 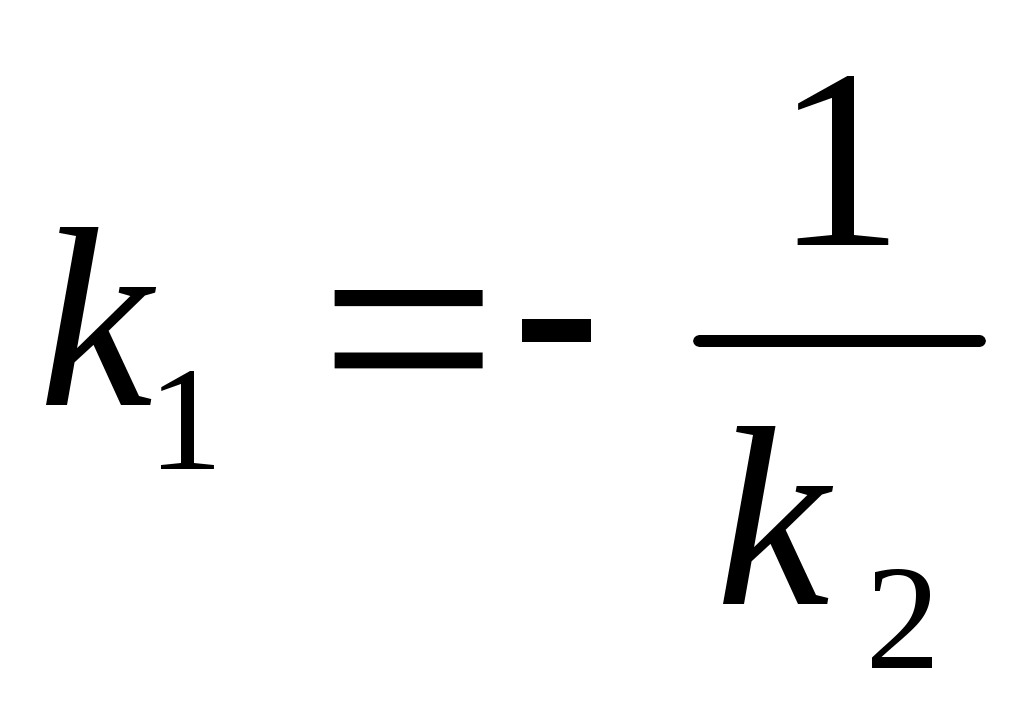 или
или 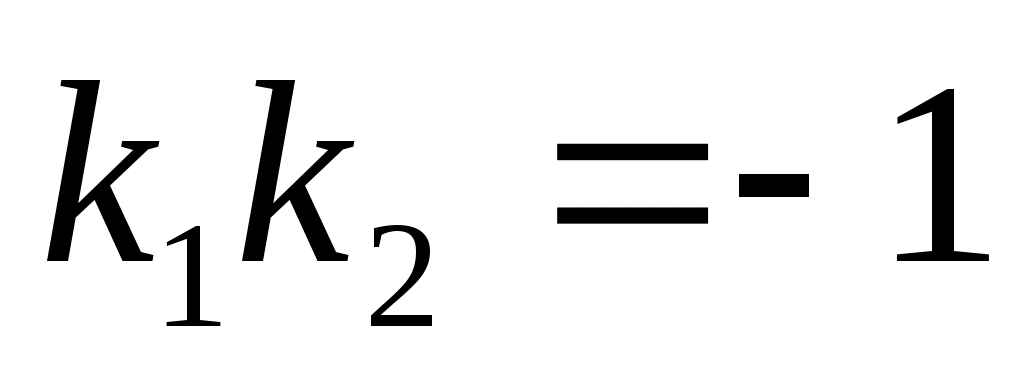 .
.
Справедливо так же и обратное утверждение.
Т.о., для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.
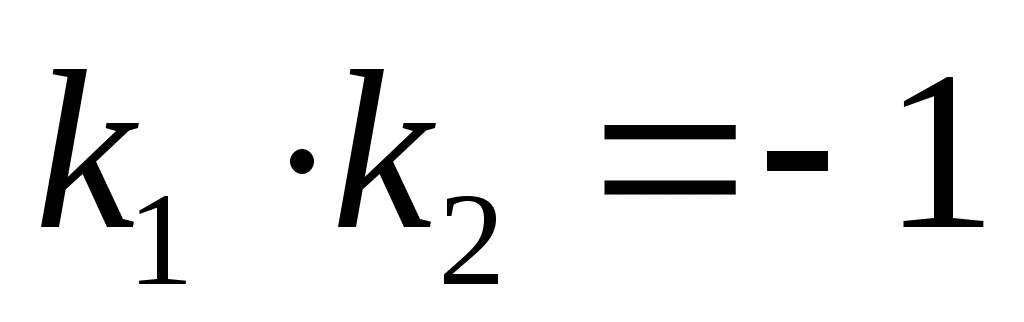 - условие перпендикулярности двух прямых.
- условие перпендикулярности двух прямых.
Если две прямые заданы уравнениями в общем виде: и ,то учитывая их угловые коэффициенты и , условие параллельности прямых имеет вид: .
Следовательно, условием параллельности прямых, заданных общими уравнениями является пропорциональность коэффициентов при переменных.
Условие перпендикулярности прямых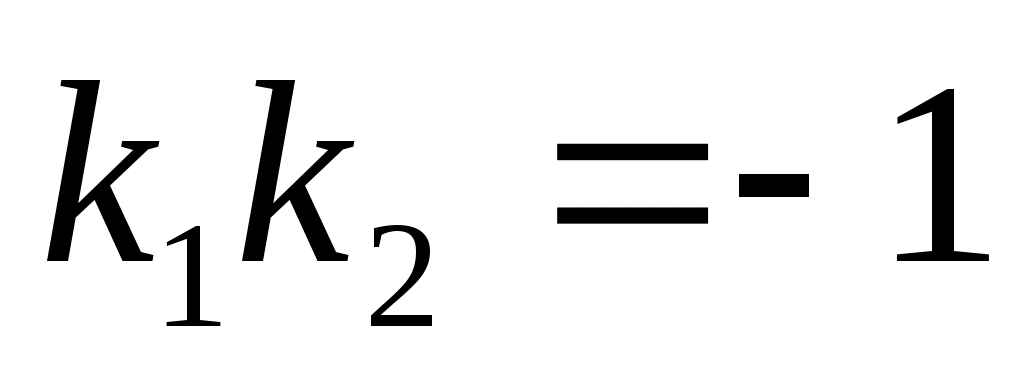 в этом случае примет вид
в этом случае примет вид 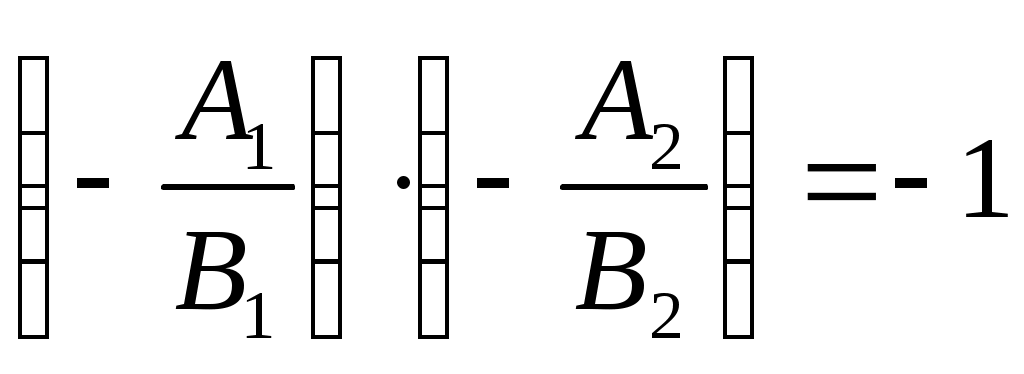 или
или 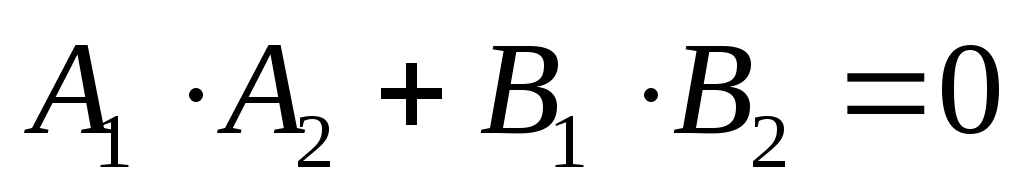 ,
,
Т.е. условием перпендикулярности двух прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных х и у.
16. Предел последовательности при и предел функции при
и предел функции при  . Признаки существования предела (с доказательством теоремы о пределе промежуточной функции).
. Признаки существования предела (с доказательством теоремы о пределе промежуточной функции).
Предел числовой последовательности
Определение. Если по некоторому закону каждому натуральному числу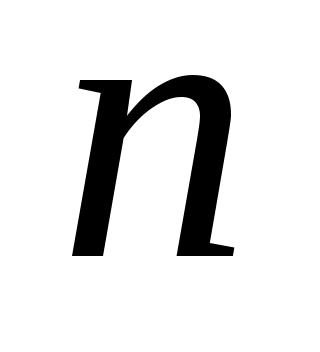 поставлено в соответствие вполне определенное число
поставлено в соответствие вполне определенное число 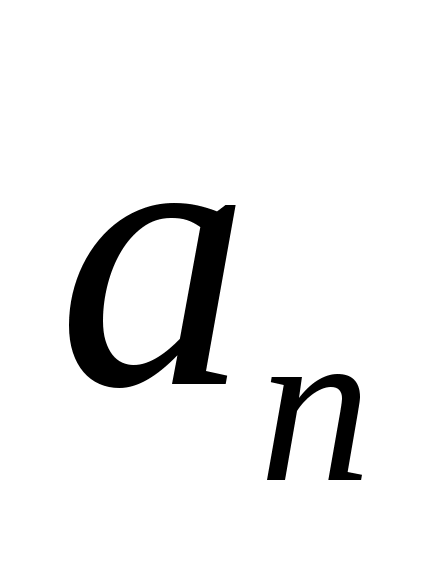 , то говорят, что задана числовая последовательность
, то говорят, что задана числовая последовательность 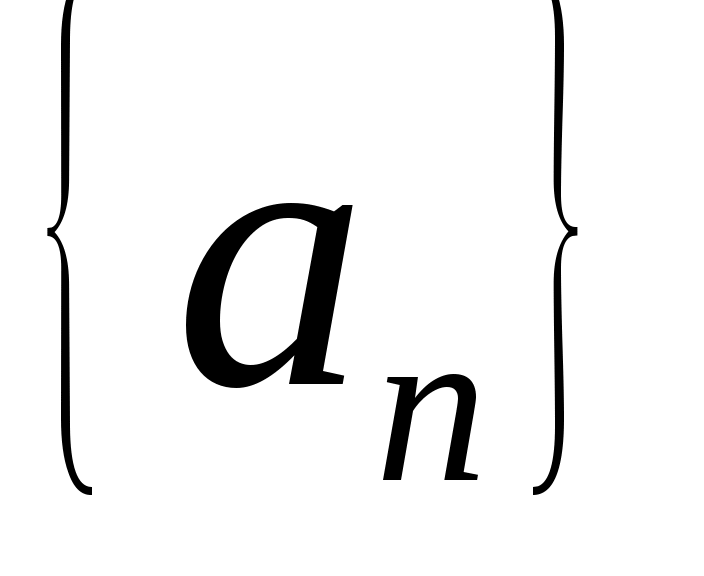 :
:
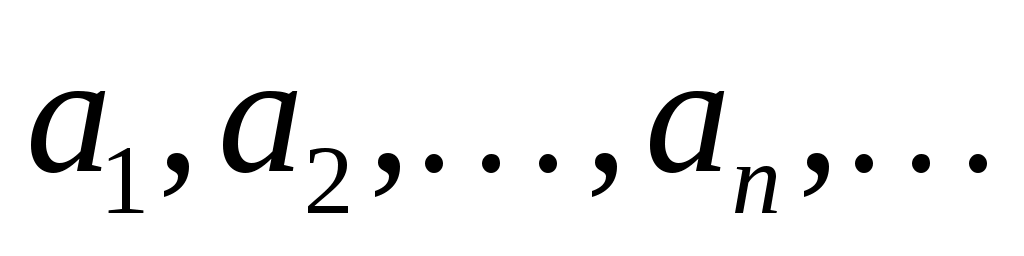 .
.
Другими словами, числовая последовательность - это функция натурального аргумента: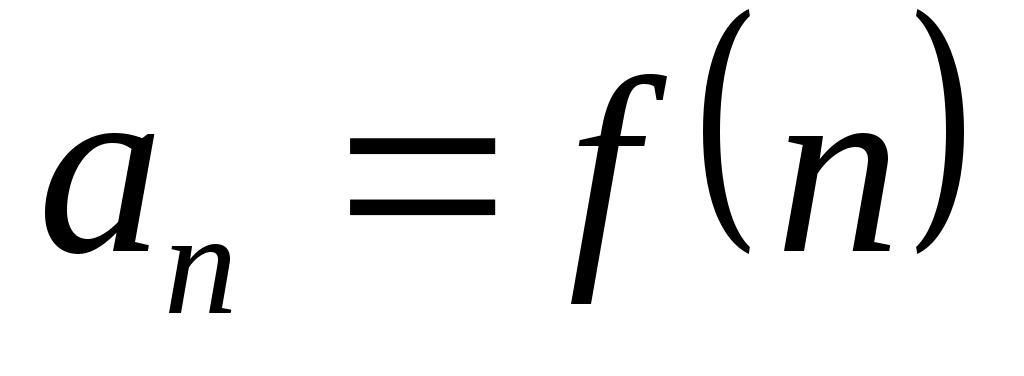 .
.
Числа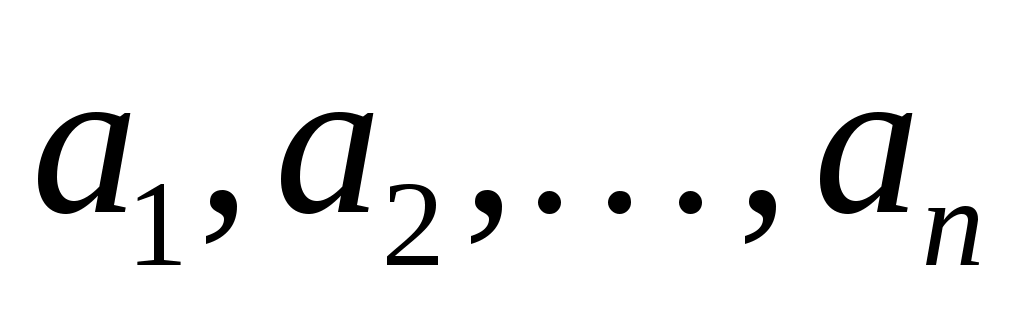 называются членами последовательности, а число
называются членами последовательности, а число 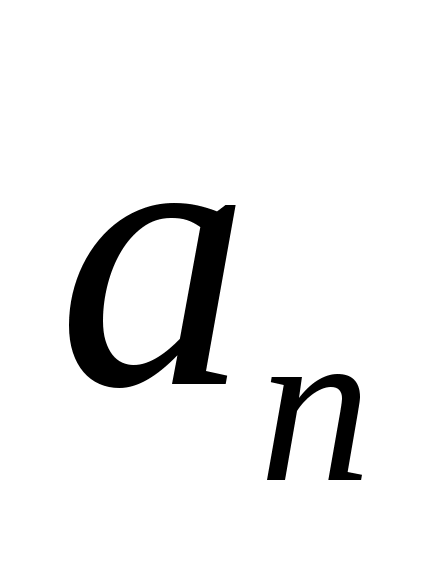 - общим или
- общим или 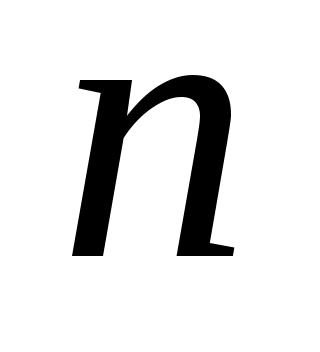 -м членом данной последовательности.
-м членом данной последовательности.
Примеры числовых последовательностей:
1)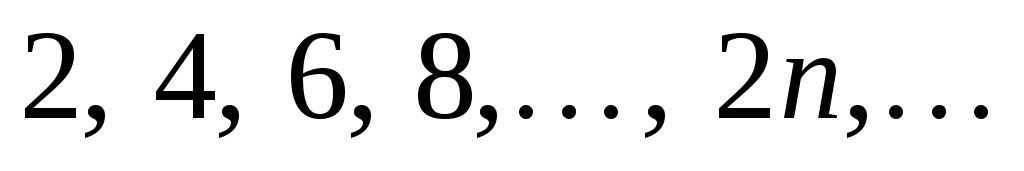 (монотонная, неограниченная),
(монотонная, неограниченная),
2)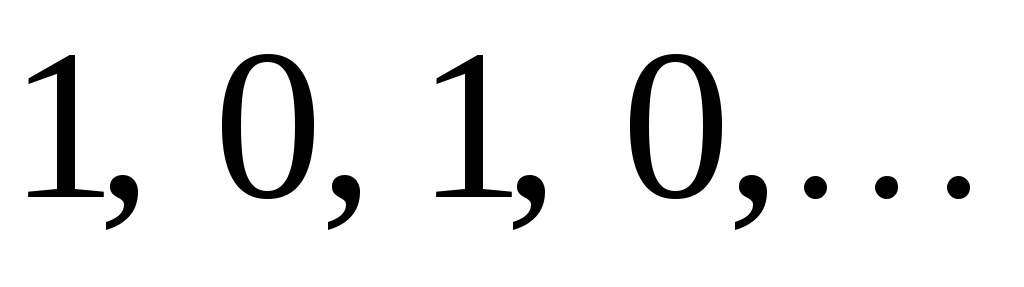 (не монотонная, ограниченная)
(не монотонная, ограниченная)
3)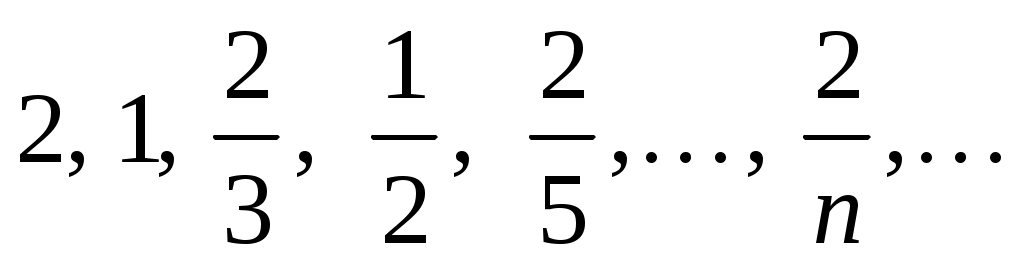
Рассмотрим числовую последовательность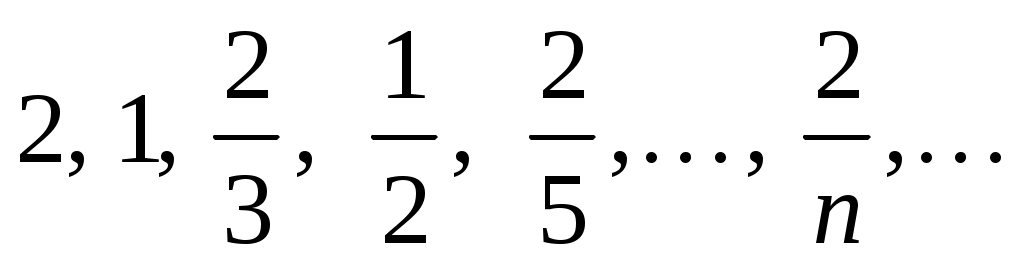 , изобразив ее точками на числовой оси (рис.4.1):
, изобразив ее точками на числовой оси (рис.4.1):
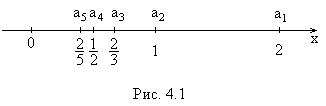
Видно, что члены последовательности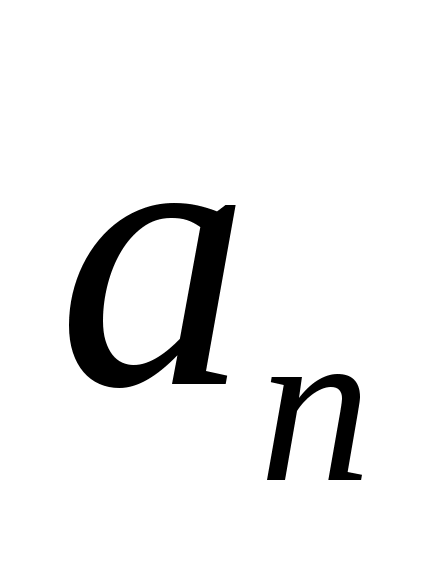 с ростом
с ростом 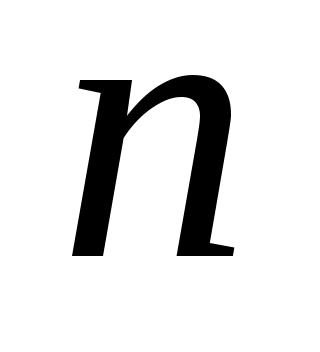 как угодно близко приближаются к 0. При этом абсолютная величина разности
как угодно близко приближаются к 0. При этом абсолютная величина разности 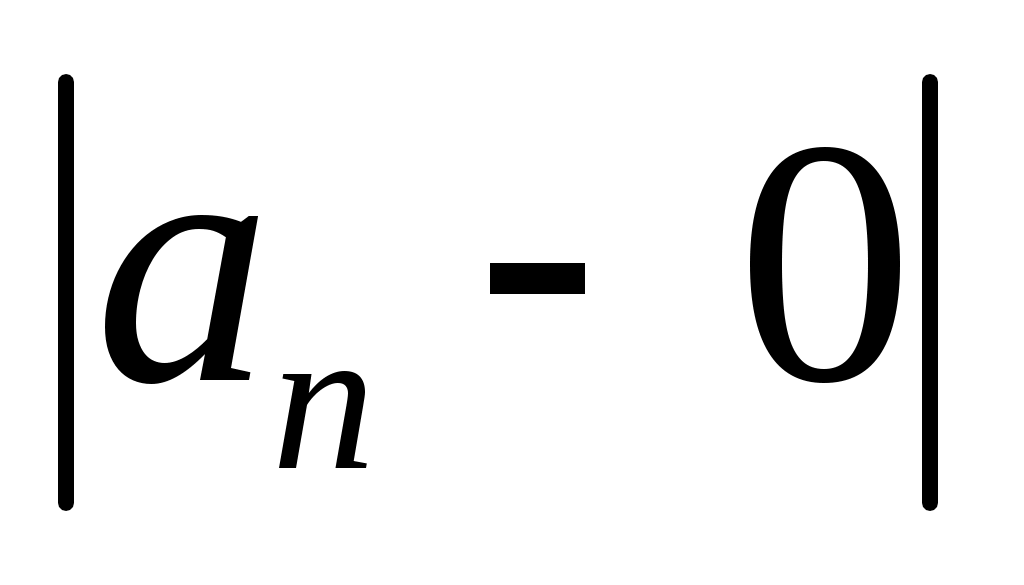 становится все меньше и меньше.
становится все меньше и меньше.
Определение. Число называется пределом числовой последовательности
называется пределом числовой последовательности 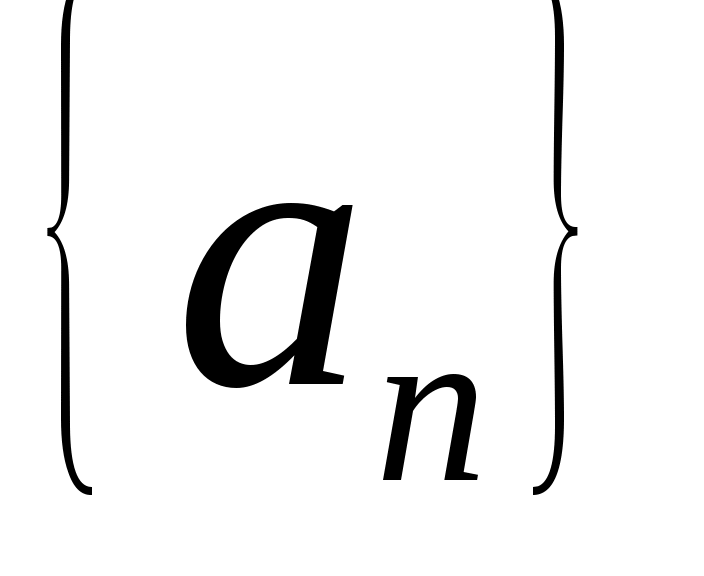 , если для любого, даже сколь угодно малого положительного числа
, если для любого, даже сколь угодно малого положительного числа 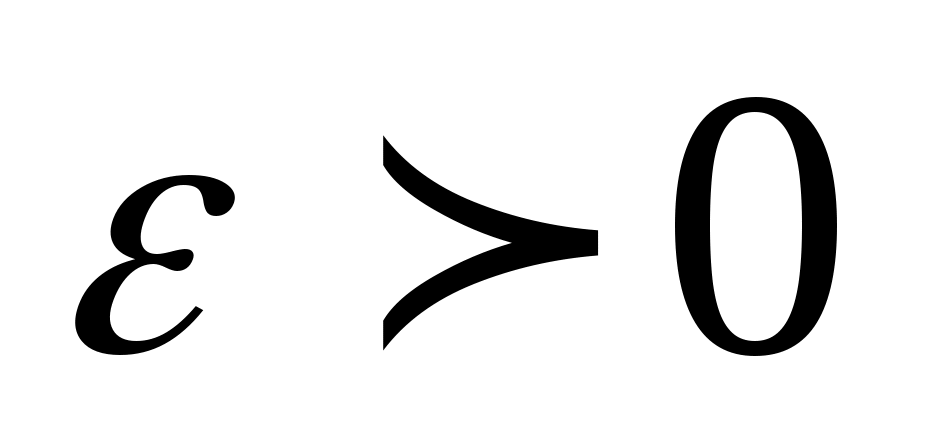 , найдется такой
, найдется такой  (зависящий от
(зависящий от 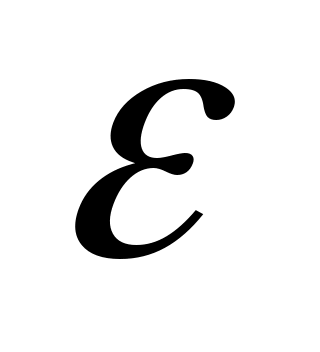 ), что для всех членов последовательности с номерами
), что для всех членов последовательности с номерами 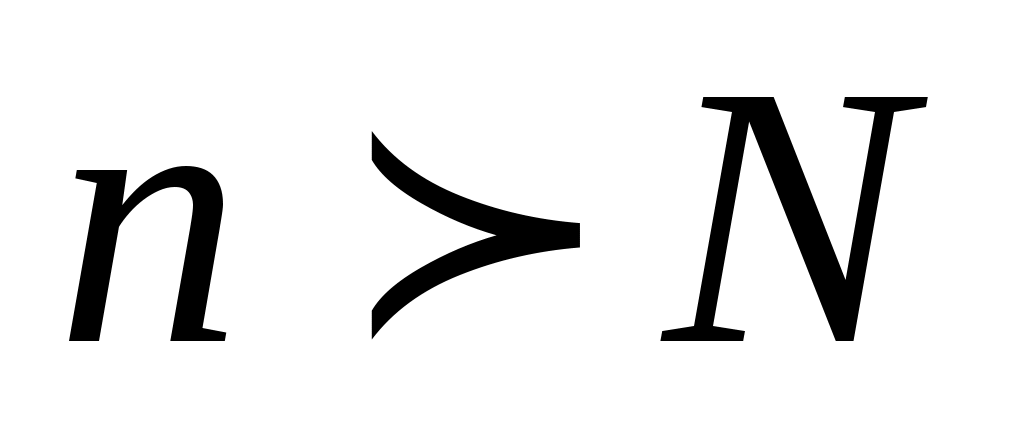 верно неравенство:
верно неравенство:
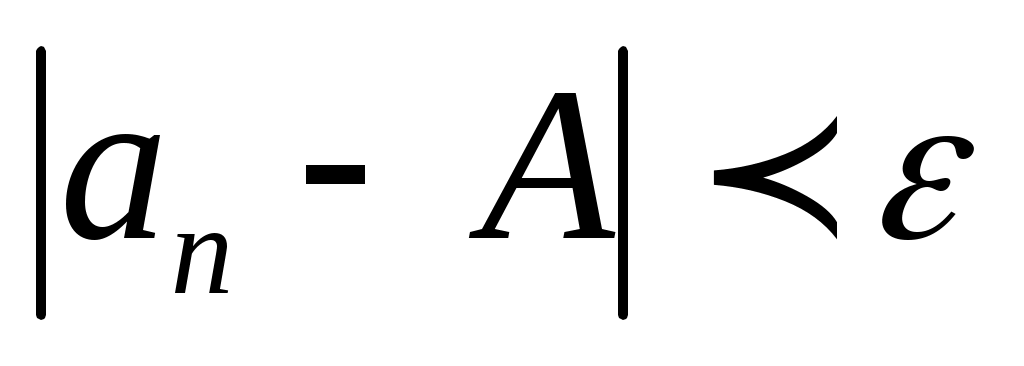 .
.
Обозначают: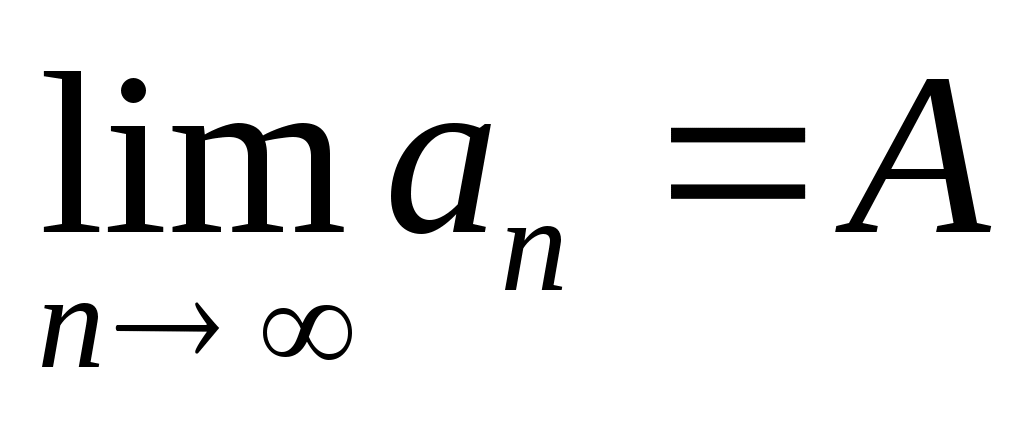 . Или
. Или  при
при  .
.
Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
Предел функции в бесконечности и в точке
Предел функции в бесконечности: С понятием предела числовой последовательности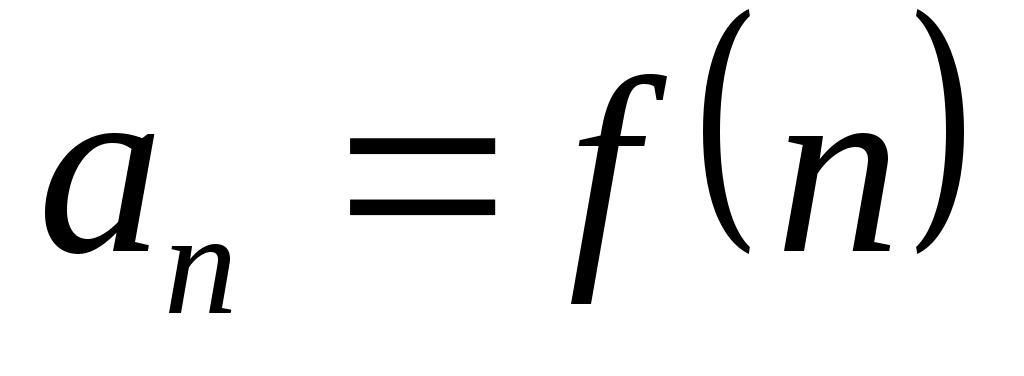 тесно связано понятие предела функции
тесно связано понятие предела функции 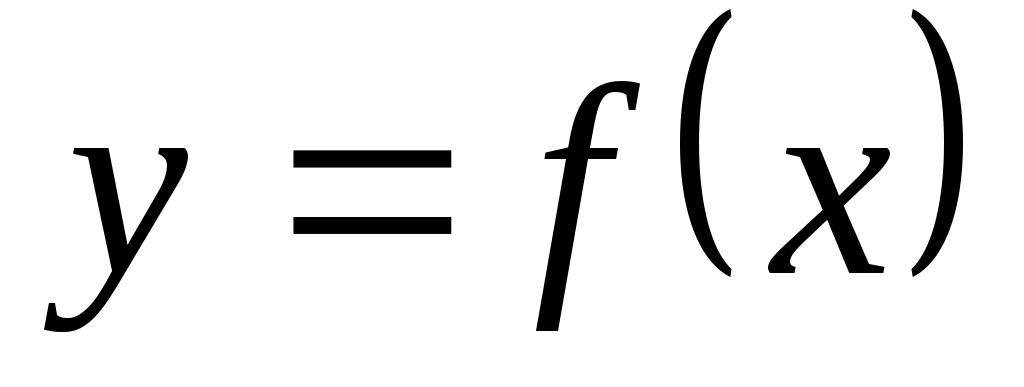 в бесконечности. Если в первом случае переменная
в бесконечности. Если в первом случае переменная 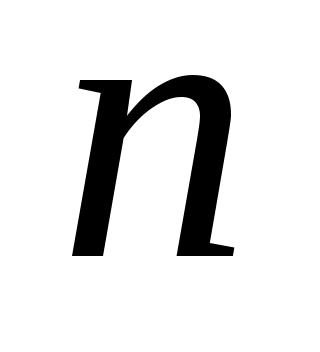 возрастая, принимает лишь целые значения, то во втором случае переменная
возрастая, принимает лишь целые значения, то во втором случае переменная 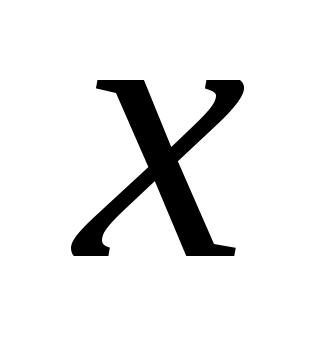 , изменяясь, принимает любые значения.
, изменяясь, принимает любые значения.
Определение. Число называется пределом функции
называется пределом функции 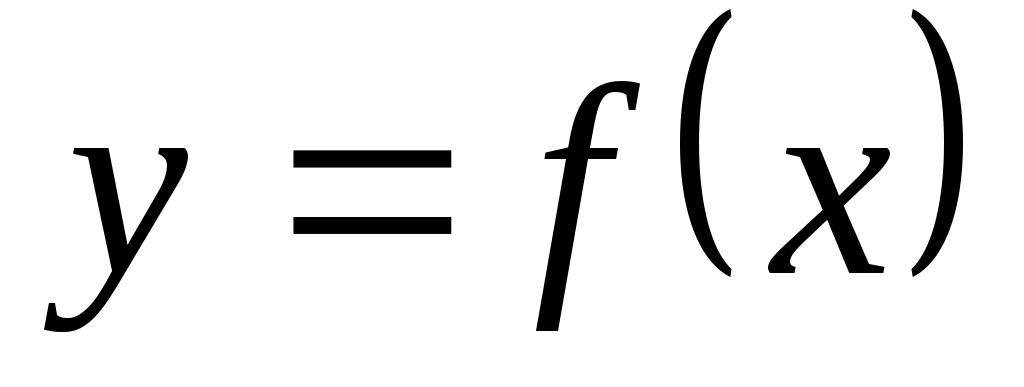 при
при 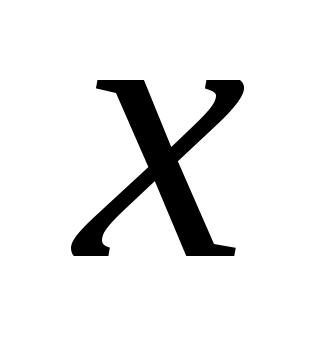 стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа
стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа 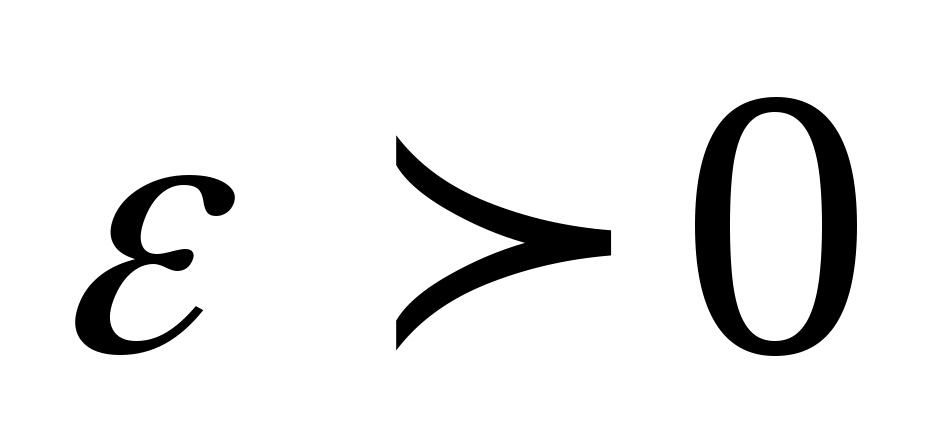
, найдется такое положительное число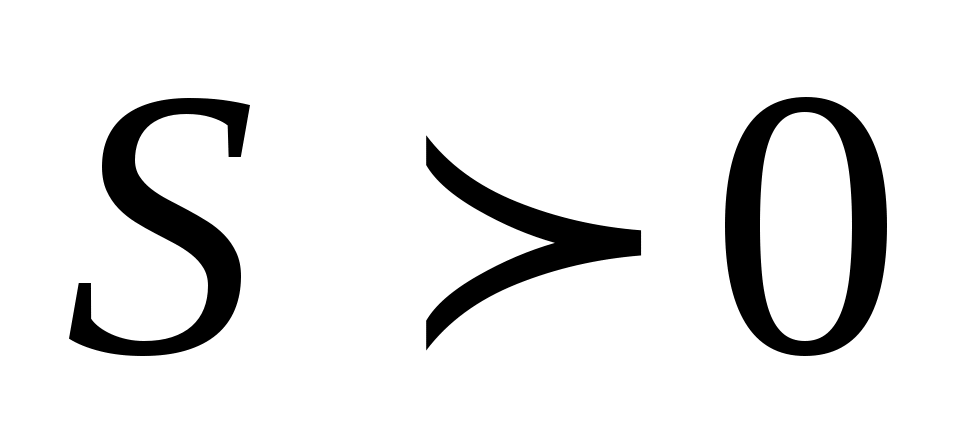 (зависящее от
(зависящее от 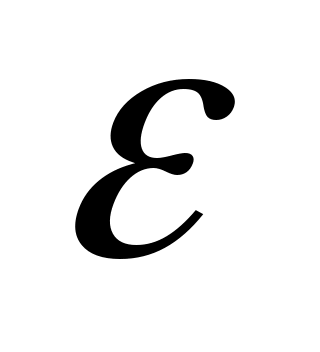 ), что для всех
), что для всех 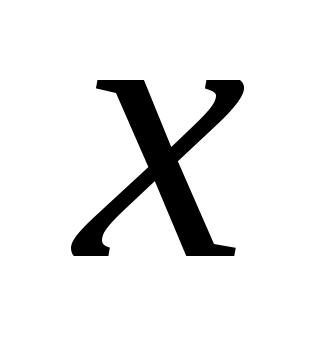 таких что
таких что 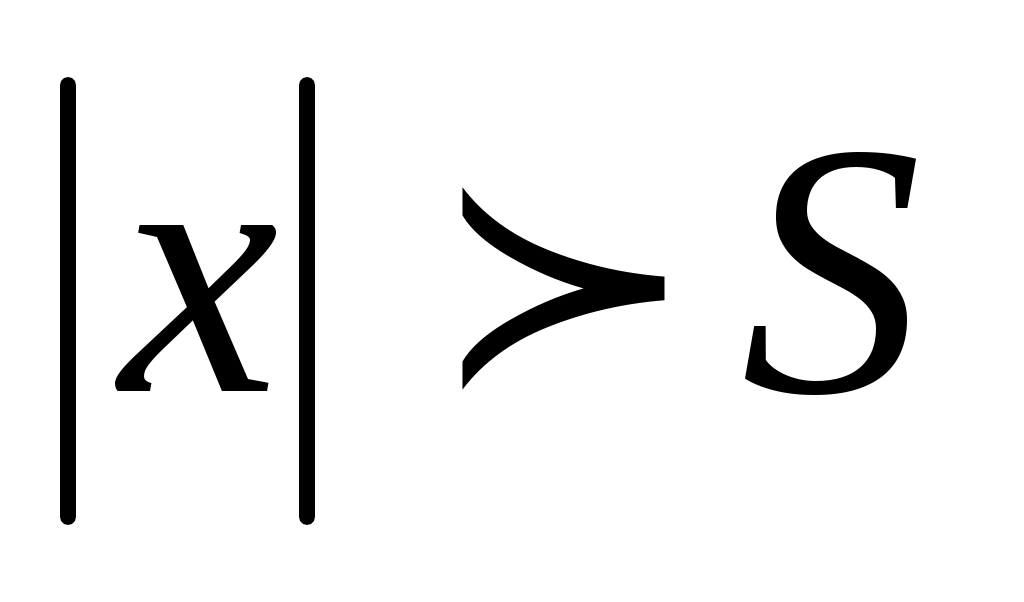 , верно неравенство:
, верно неравенство:
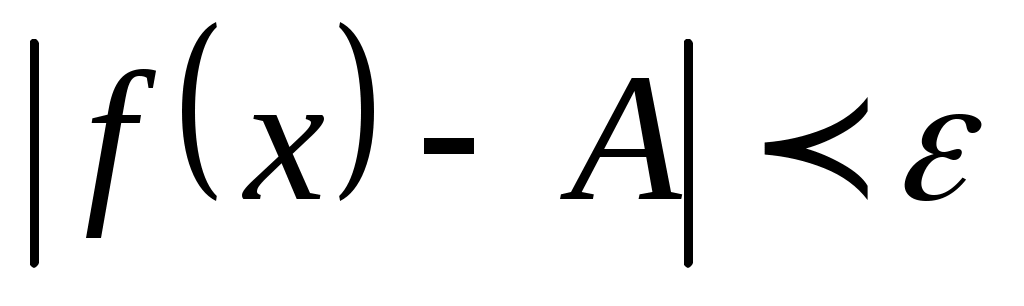 .
.
Это предел функции обозначается: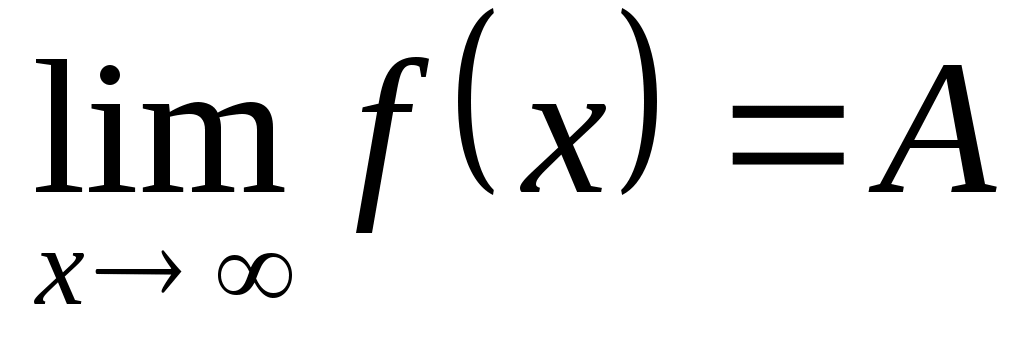 или
или 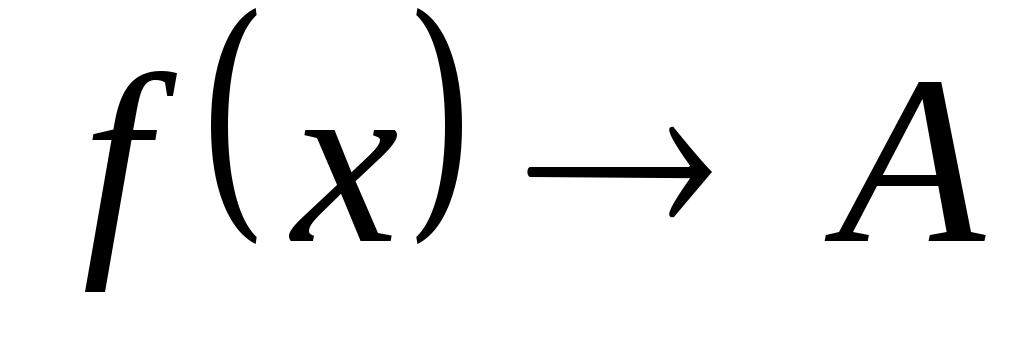 при
при  .
.
Можно сформулировать понятие предела при стремлении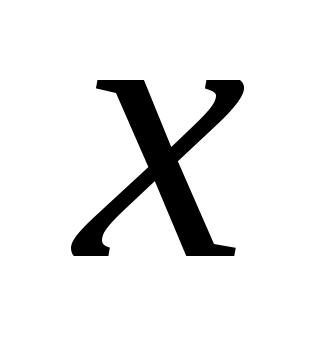 к бесконечности определенного знака, т.е. при
к бесконечности определенного знака, т.е. при  и при
и при 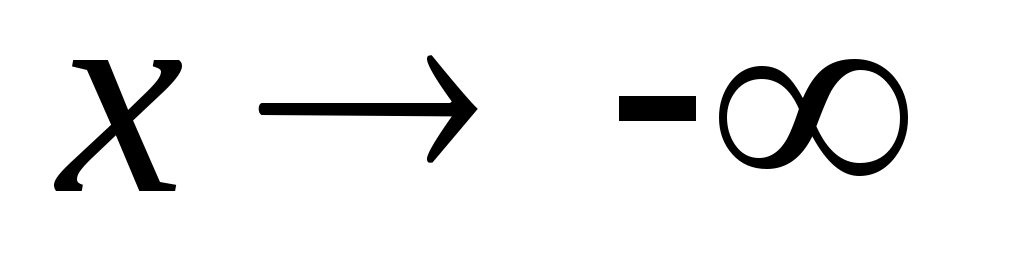 . В первом случае основное неравенство:
. В первом случае основное неравенство: 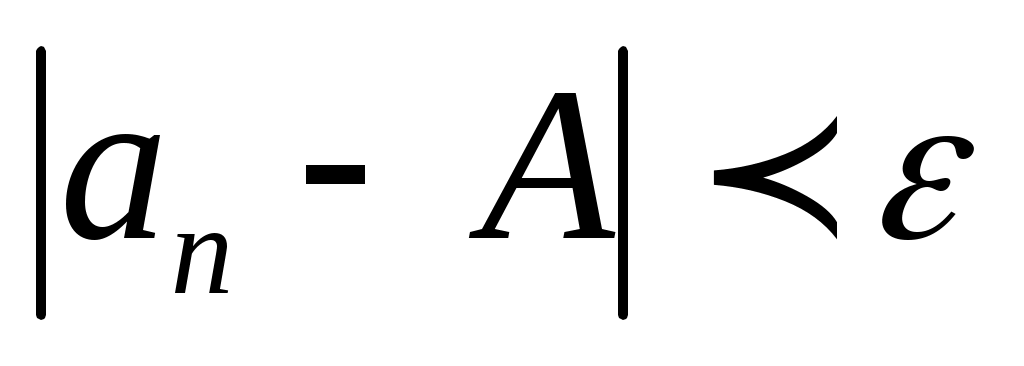 должно выполнятся для всех
должно выполнятся для всех 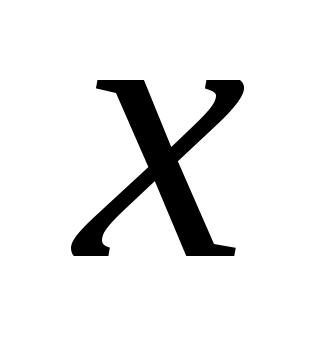 таких, что
таких, что 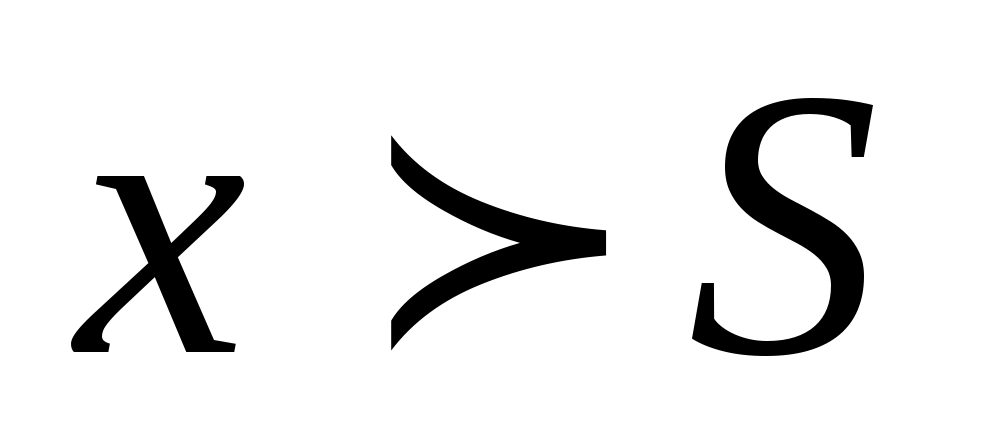 , а во втором – для всех
, а во втором – для всех 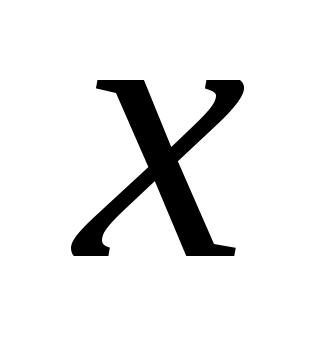 таких, что
таких, что 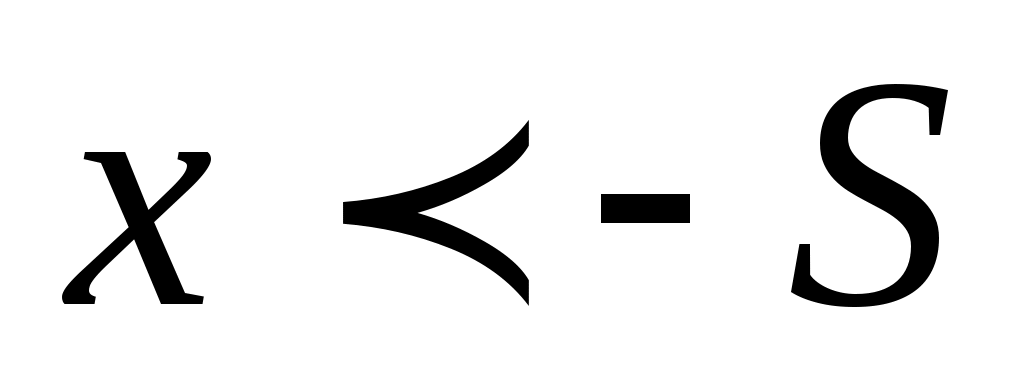 .
.
Предел функции в точке: Пусть функция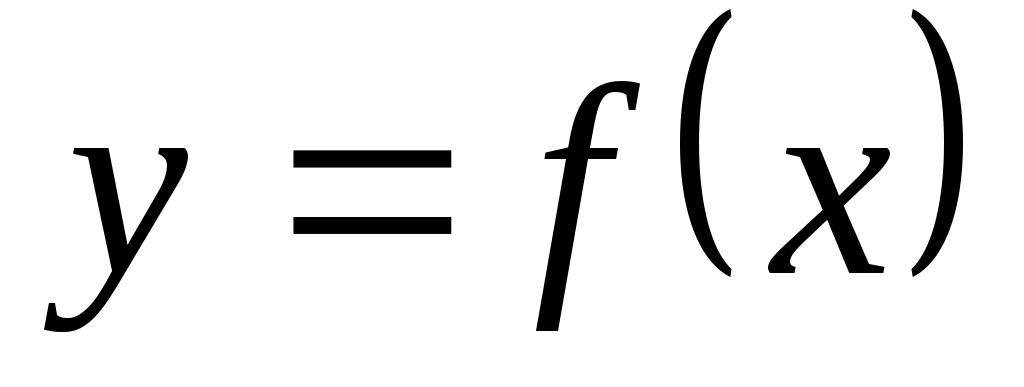 задана в некоторой окрестности точки
задана в некоторой окрестности точки 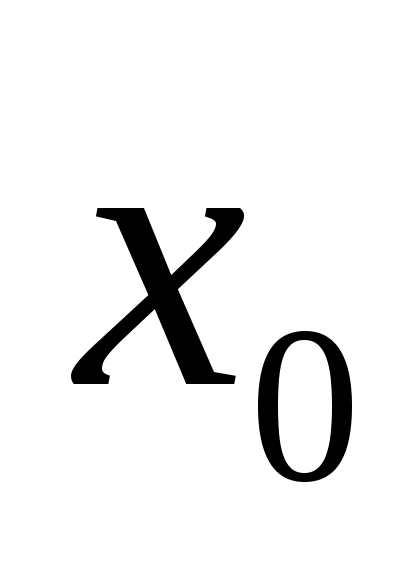 , кроме, быть может, самой точки
, кроме, быть может, самой точки 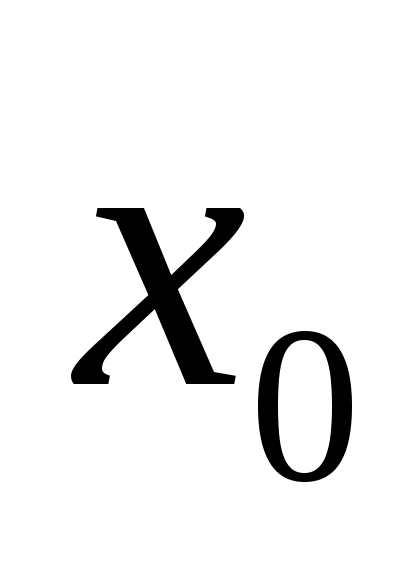 .
.
Определение. Число называется пределом функции
называется пределом функции 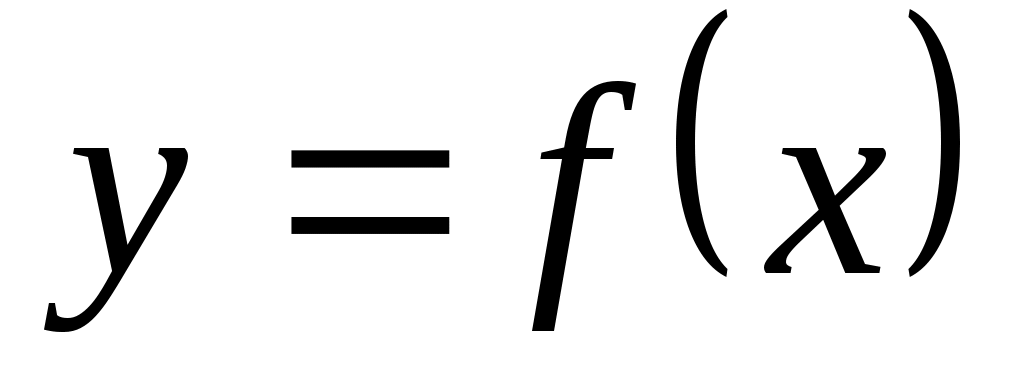 при
при 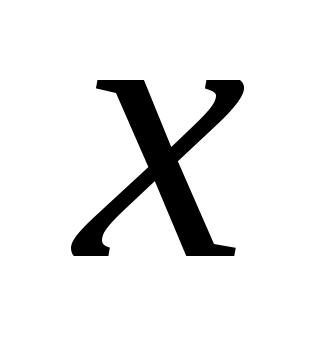 стремящемся к
стремящемся к
15. Общее уравнение прямой на плоскости, его исследование. Условия параллельности и перпендикулярности прямых.
Общее уравнение прямой и его исследование
Рассмотрим уравнение прямой с угловым коэффициентом
общее уравнение прямой, где и не равны нулю одновременно, т.е.
Рассмотрим частные случаи уравнения (3.6).
-
Пусть . Тогда уравнение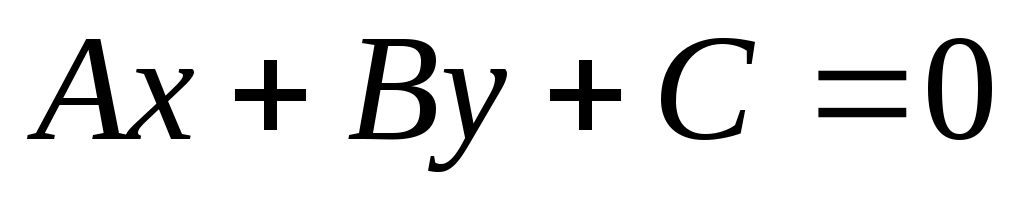 можно записать в виде: . Обозначим .
можно записать в виде: . Обозначим .
Если , , то получим (уравнение прямой с угловым коэффициентом);
Если , , то (уравнение прямой, проходящей через начало координат);
Если , , то (уравнение прямой, параллельной оси Оу);
Если , , то (уравнение оси Ох).
-
Пусть , . Тогда уравнение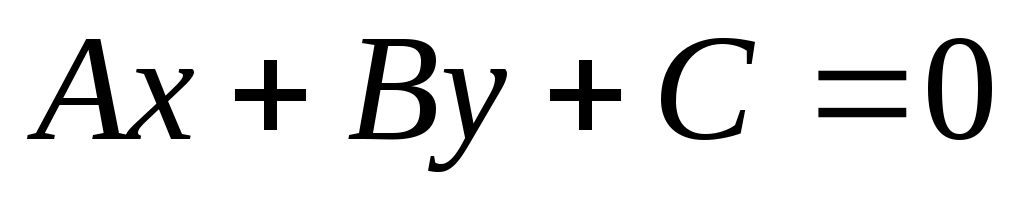 примет вид . Обозначим .
примет вид . Обозначим .
Если , то получим (уравнение прямой, параллельной оси Оу);
Если , то (уравнение оси Оу).
Т.о., при любых значениях коэффициентов , (не равных одновременно нулю) и уравнение
Условия параллельности и перпендикулярности двух прямых:
Если прямые и параллельны, то угол и , откуда из формулы угла между двумя прямыми
. И наоборот, если , то по этой же формуле и .
Т.о., равенство угловых коэффициентов является необходимым и достаточным условием параллельности 2х прямых.
Если прямые перпендикулярны, то , при этом
Справедливо так же и обратное утверждение.
Т.о., для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.
Если две прямые заданы уравнениями в общем виде: и ,то учитывая их угловые коэффициенты и , условие параллельности прямых имеет вид: .
Следовательно, условием параллельности прямых, заданных общими уравнениями является пропорциональность коэффициентов при переменных.
Условие перпендикулярности прямых
Т.е. условием перпендикулярности двух прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных х и у.
16. Предел последовательности при
Предел числовой последовательности
Определение. Если по некоторому закону каждому натуральному числу
Другими словами, числовая последовательность - это функция натурального аргумента:
Числа
Примеры числовых последовательностей:
1)
2)
3)
Рассмотрим числовую последовательность
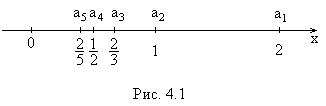
Видно, что члены последовательности
Определение. Число
Обозначают:
Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
Предел функции в бесконечности и в точке
Предел функции в бесконечности: С понятием предела числовой последовательности
Определение. Число
, найдется такое положительное число
Это предел функции обозначается:
Можно сформулировать понятие предела при стремлении
Предел функции в точке: Пусть функция
Определение. Число


