Файл: 1. Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами умножение на число, сложение, умножение матриц.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.04.2024
Просмотров: 93
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Е сли точка передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты называются текущими координатами.
сли точка передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты называются текущими координатами.
Любую линию в принципе можно выразить соответствующим уравнением. Однако не всякое уравнение на определяет на плоскости некоторую линию.
Например: определяет только одну точку (0;0);
не определяет никакого множества точек, т.к. левая часть уравнения не может равняться нулю.
Чтобы убедится, лежит ли точка на данной линии , надо проверить, удовлетворяют ли координаты этой точки уравнению .
Уравнения линии могут быть самыми различными, однако надо отметить, что не каждое уравнение имеет геометрический образ в виде линии.
Чтобы определить взаимное расположение 2-х линий, необходимо знать уравнений этих линий. Если система этих уравнений совместна, то линии имеют общие точки. В противном случае общих точек нет. Число общих точек равно числу решений системы уравнений
Например, прямая линия и окружность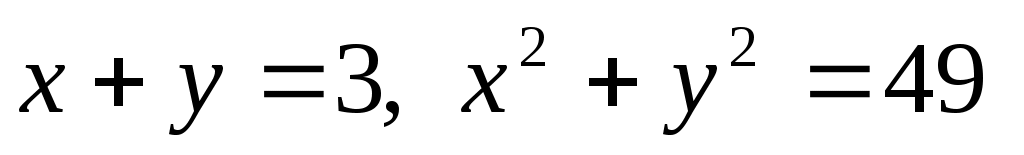 имеют 2 общие точки, так как система из этих уравнений имеет два решения:
имеют 2 общие точки, так как система из этих уравнений имеет два решения:
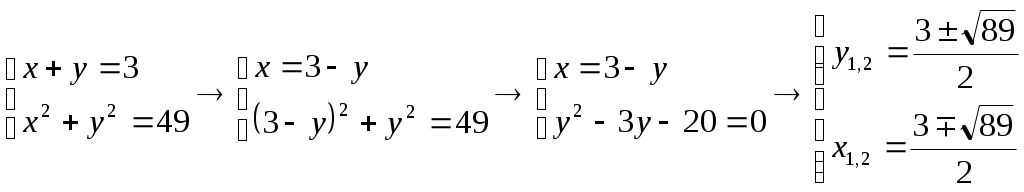 .
.
В декартовой системе координат рассмотрим прямую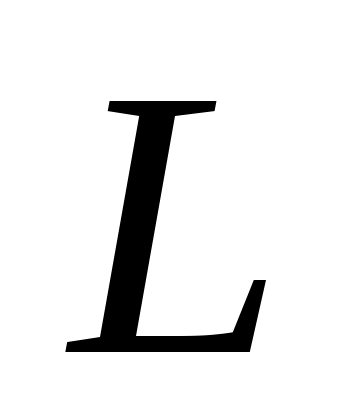 , расположенную под углом
, расположенную под углом 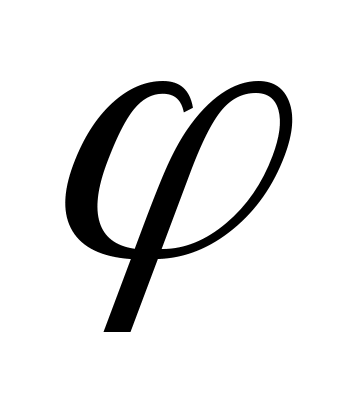 к оси
к оси 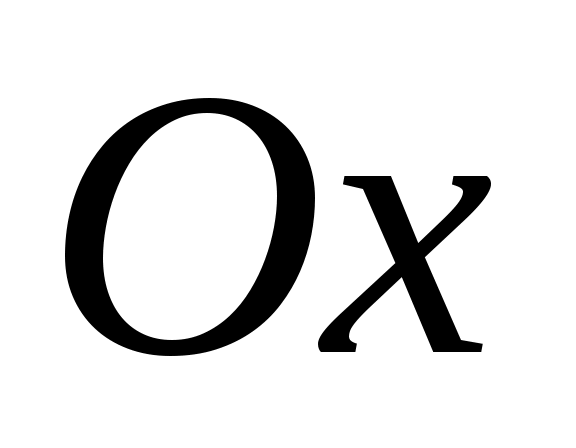 (рис. 3.7).
(рис. 3.7).
Полученное уравнение называется уравнением прямой с угловым коэффициентом.
Частные случаи уравнения (3.1):


Уравнение прямой, проходящей через две заданные точки
Из последнего равенства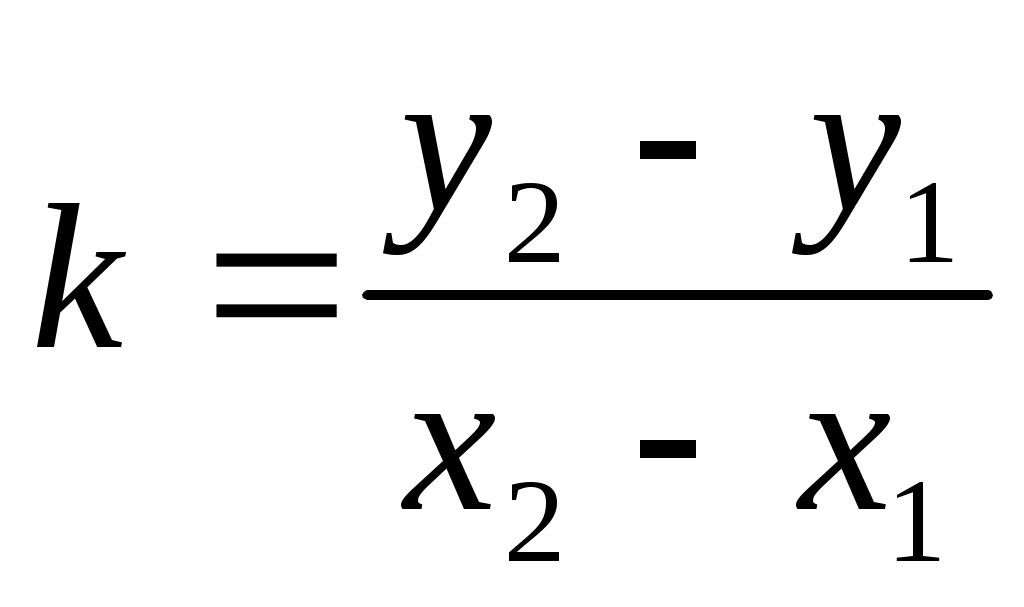 . Подставляя выражение для
. Подставляя выражение для 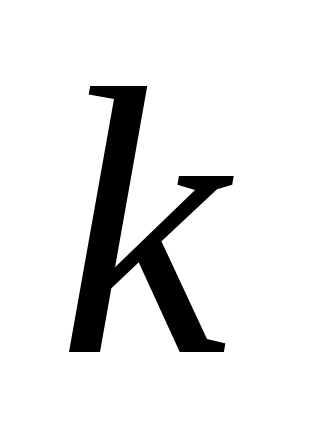 в уравнение (3.4):
в уравнение (3.4): 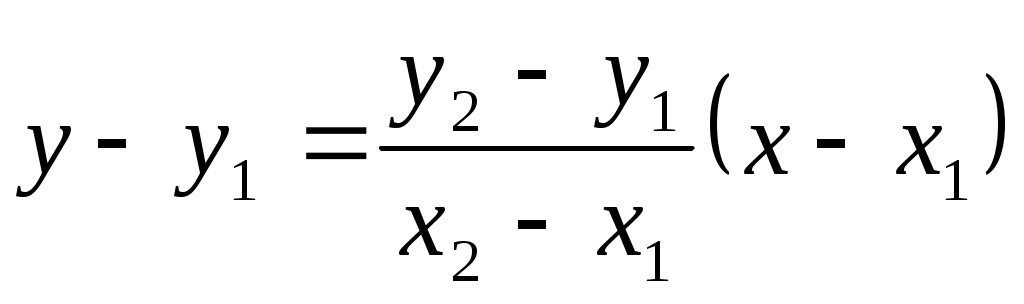 , получим уравнение прямой по двум точкам
, получим уравнение прямой по двум точкам
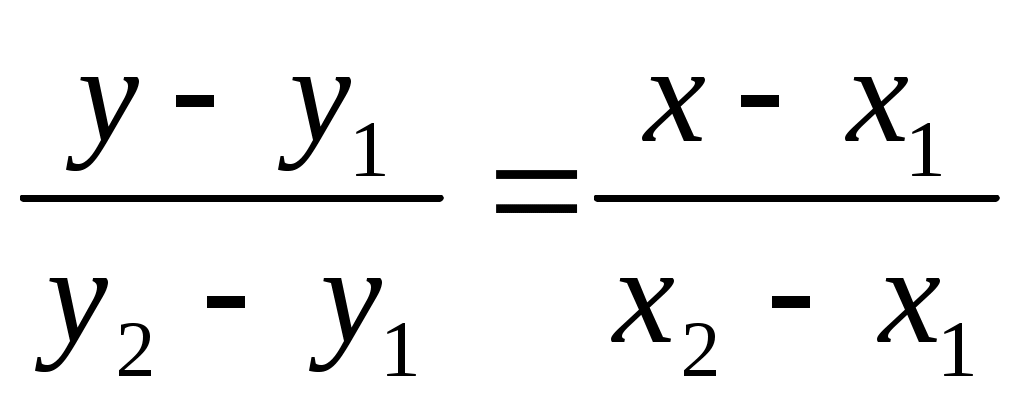 (3.5).
(3.5).
Уравнение пучка прямых
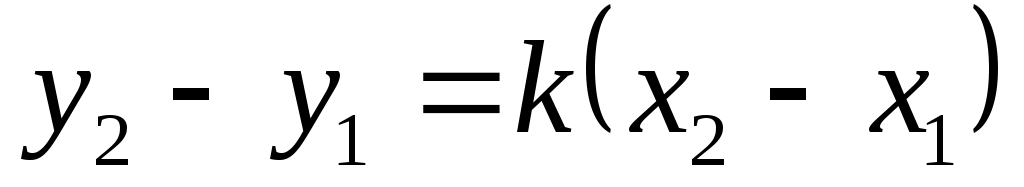
Уравнение прямой в отрезках
Уравнение называется уравнением прямой в отрезках.
Общее уравнение прямой и его исследование
Рассмотрим уравнение прямой с угловым коэффициентом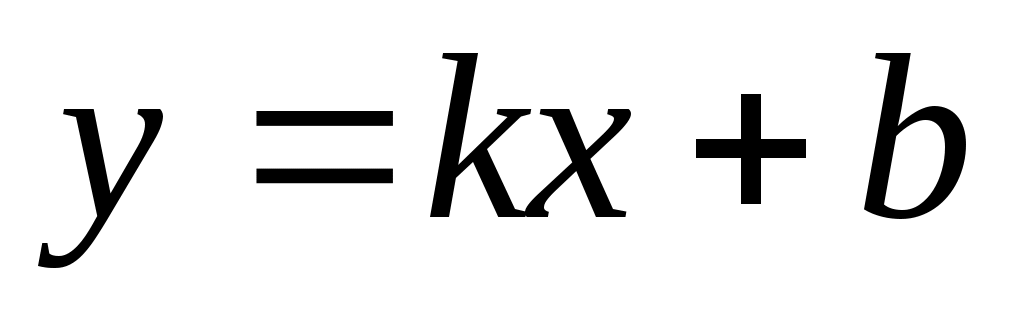 . Перенесем все слагаемые в левую часть и перепишем его в следующем виде:
. Перенесем все слагаемые в левую часть и перепишем его в следующем виде:
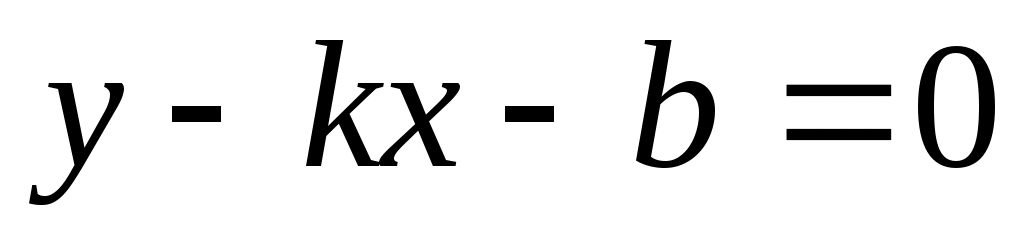 ,
,
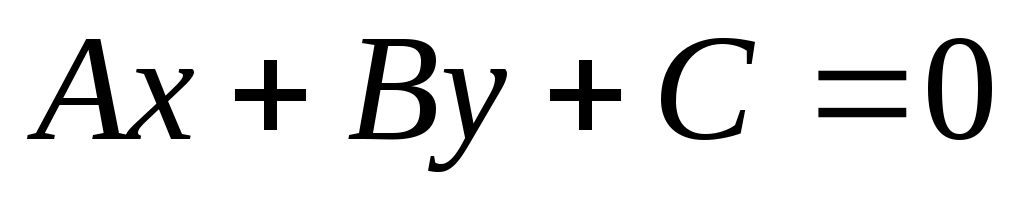 - (3.6)
- (3.6)
общее уравнение прямой, где и не равны нулю одновременно, т.е.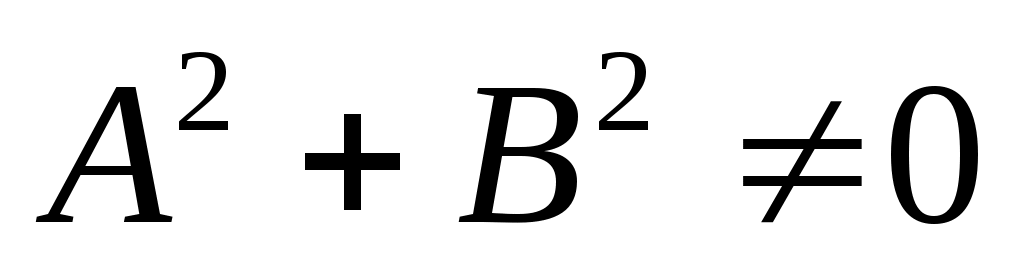 .
.
Рассмотрим частные случаи уравнения (3.6).
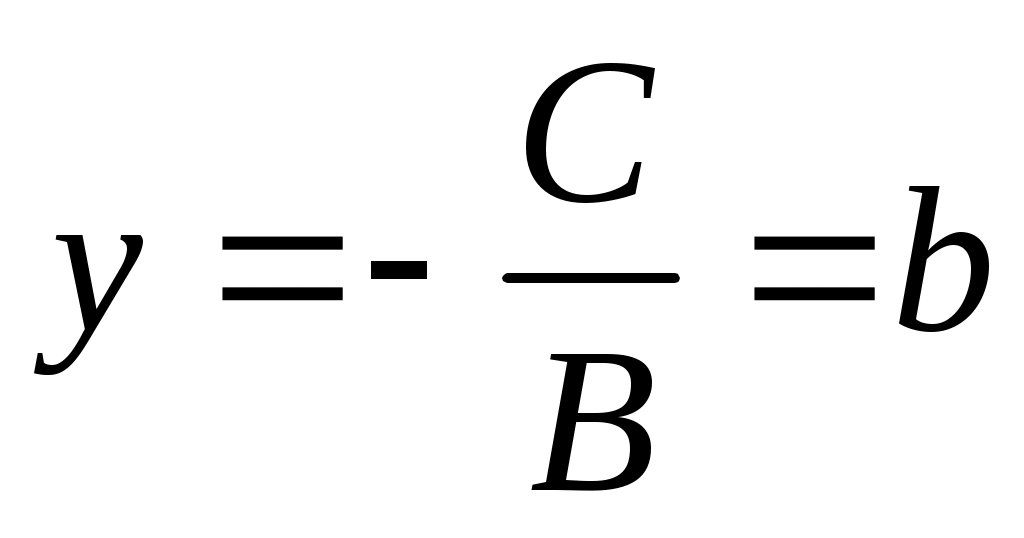 .
.
Если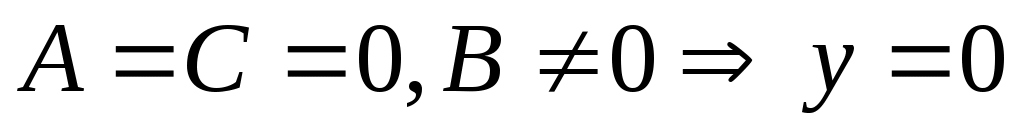 - уравнение оси
- уравнение оси 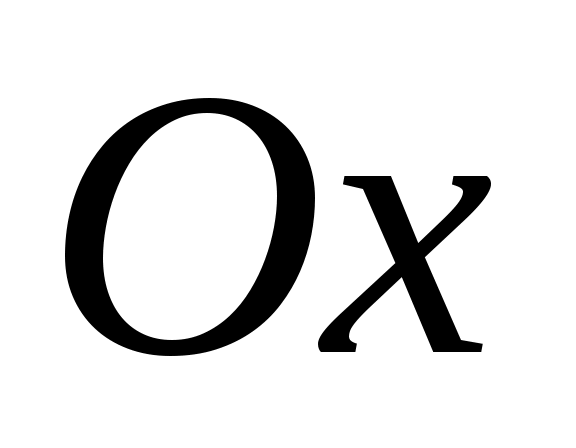 .
.
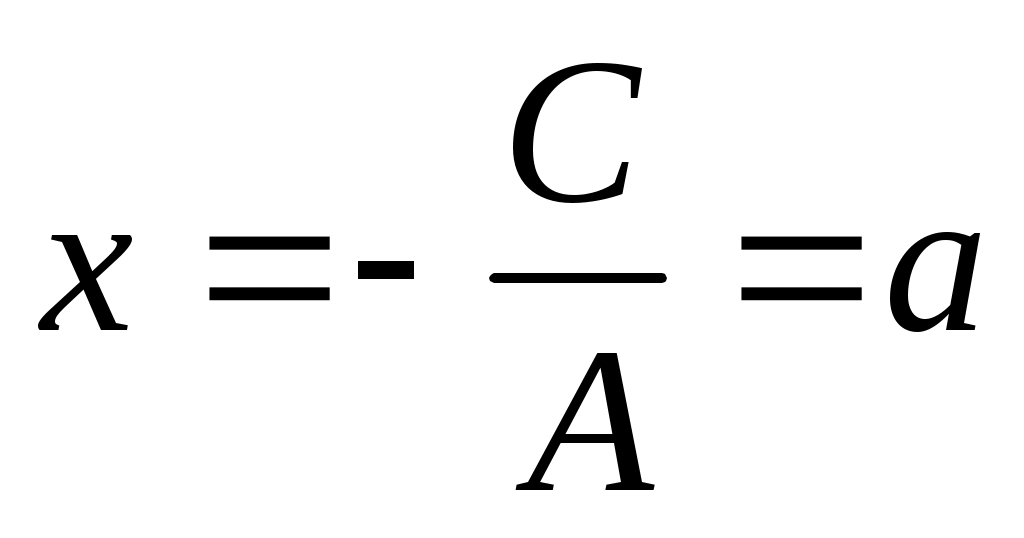 .
.
Если - уравнение оси
- уравнение оси 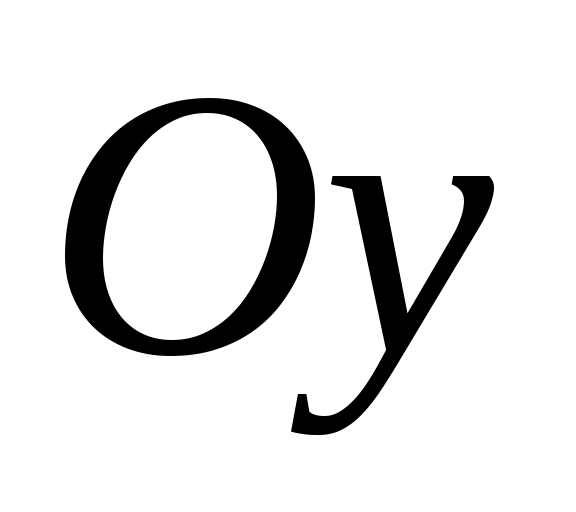 .
.
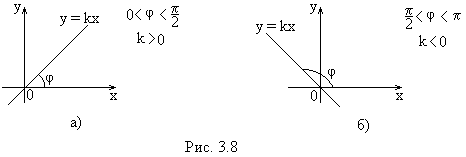
3) Если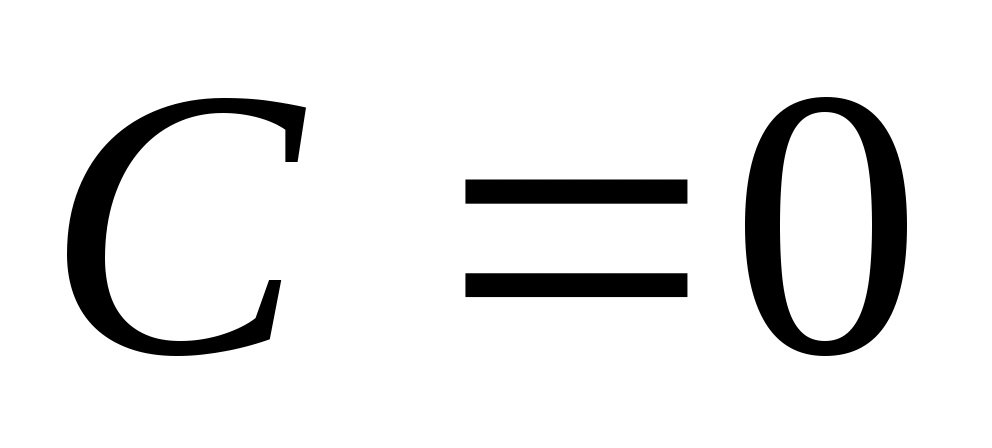 , тогда уравнение имеет вид
, тогда уравнение имеет вид 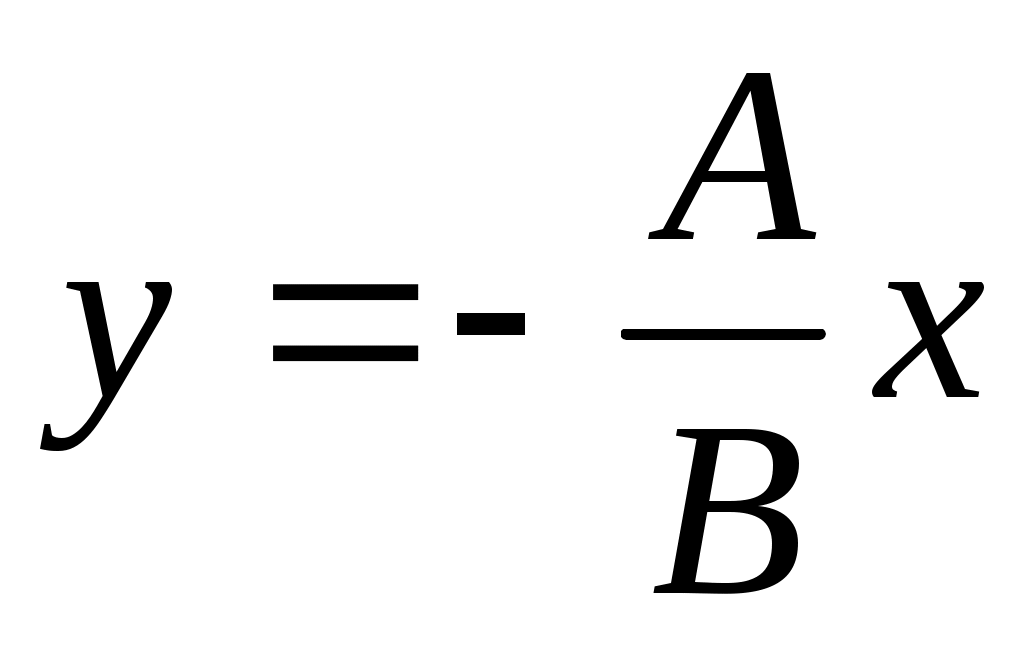 и прямая проходит через начало координат (рис. 3.8).
и прямая проходит через начало координат (рис. 3.8).
Точка пересечения прямых
Если заданы две прямые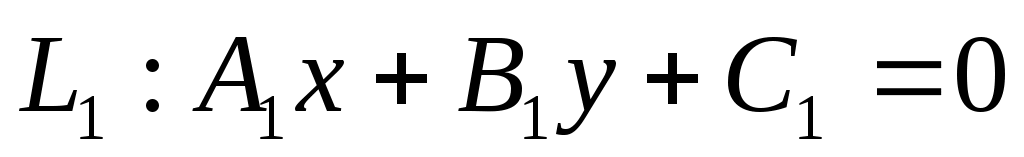 и
и 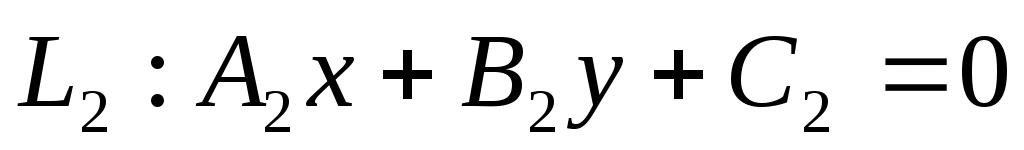 , то координаты точки их пересечения должны удовлетворять уравнению каждой прямой, т.е. они могут быть найдены из системы:
, то координаты точки их пересечения должны удовлетворять уравнению каждой прямой, т.е. они могут быть найдены из системы: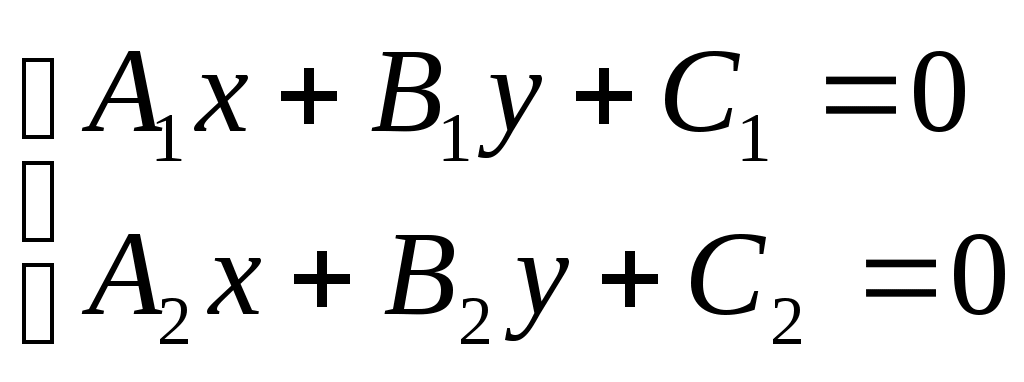 .
.
Если прямые не параллельны, т.е.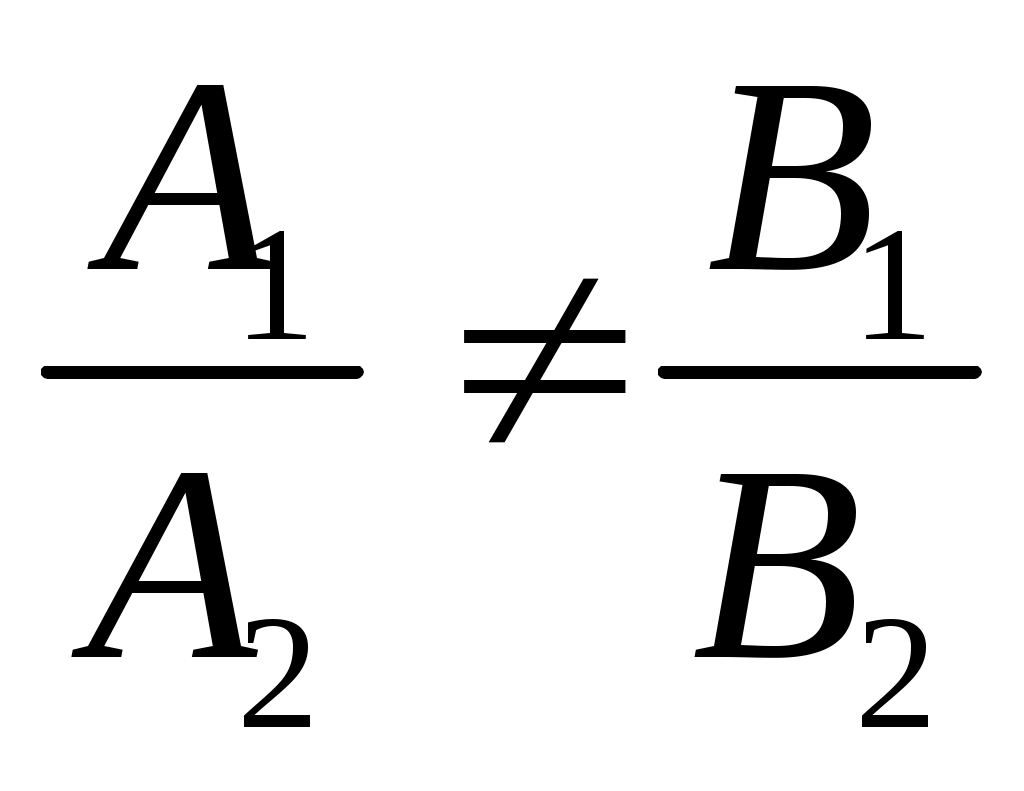
Е
 сли точка передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты называются текущими координатами.
сли точка передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии. Поэтому координаты называются текущими координатами.Любую линию в принципе можно выразить соответствующим уравнением. Однако не всякое уравнение на определяет на плоскости некоторую линию.
Например: определяет только одну точку (0;0);
не определяет никакого множества точек, т.к. левая часть уравнения не может равняться нулю.
Чтобы убедится, лежит ли точка на данной линии , надо проверить, удовлетворяют ли координаты этой точки уравнению .
Уравнения линии могут быть самыми различными, однако надо отметить, что не каждое уравнение имеет геометрический образ в виде линии.
Взаимное расположение двух линий
Чтобы определить взаимное расположение 2-х линий, необходимо знать уравнений этих линий. Если система этих уравнений совместна, то линии имеют общие точки. В противном случае общих точек нет. Число общих точек равно числу решений системы уравнений
Например, прямая линия и окружность
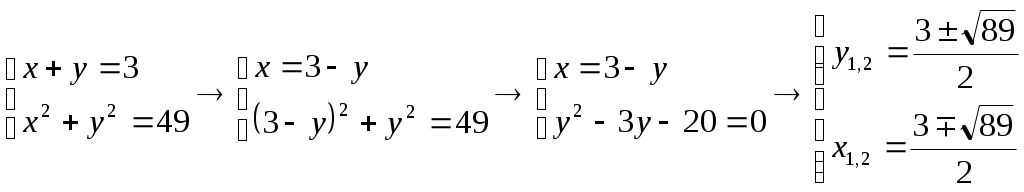 .
.Уравнение прямой на плоскости
В декартовой системе координат рассмотрим прямую
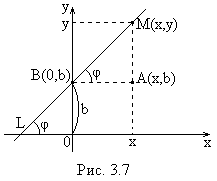 | Выберем на прямой L произвольную точку Введем угловой коэффициент прямой Из последнего равенства |
Полученное уравнение называется уравнением прямой с угловым коэффициентом.
Частные случаи уравнения (3.1):

-
Если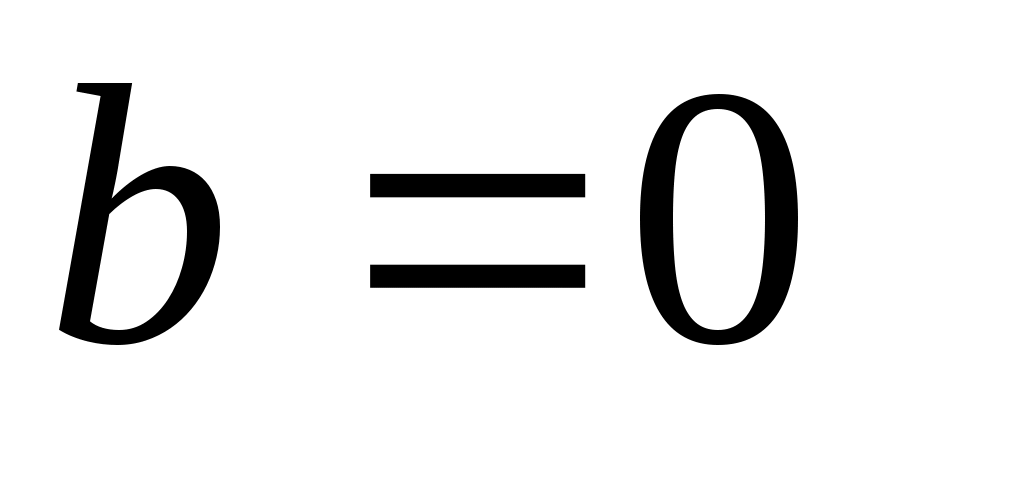 , тогда
, тогда 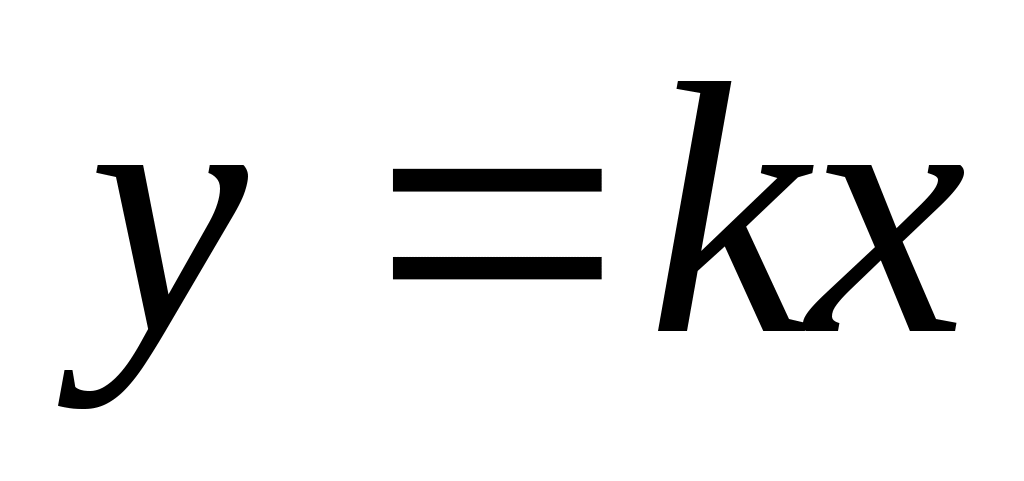 и уравнение (3.1) представляет прямую, проходящую через начало координат под углом
и уравнение (3.1) представляет прямую, проходящую через начало координат под углом 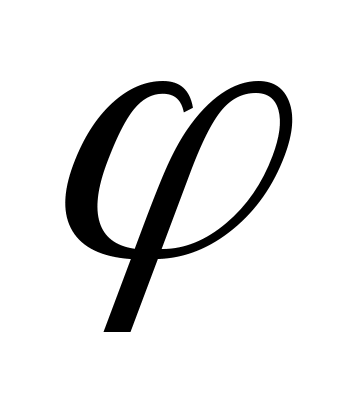 к оси
к оси 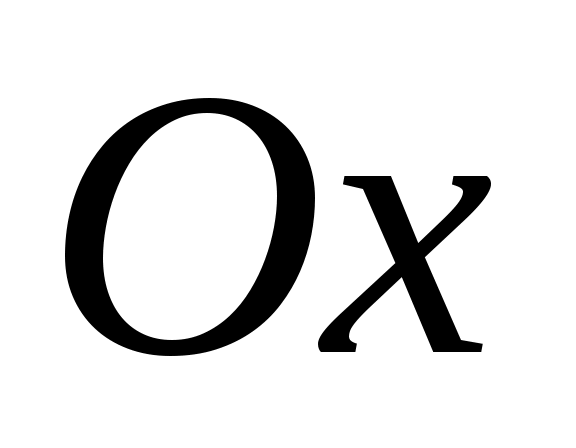 (рис. 3.8).
(рис. 3.8).

-
Если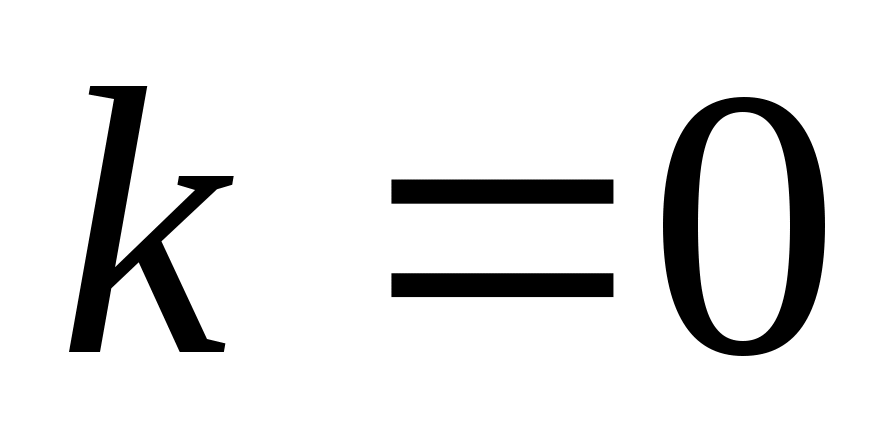 (т.е.
(т.е. 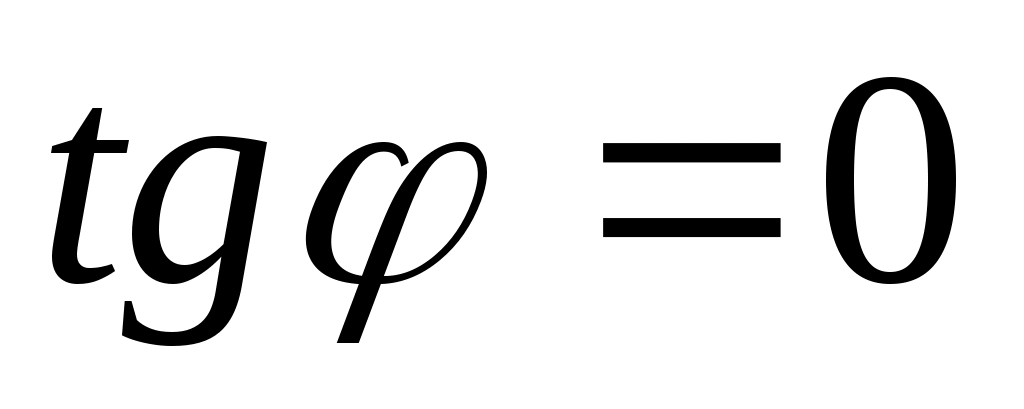 ), тогда
), тогда 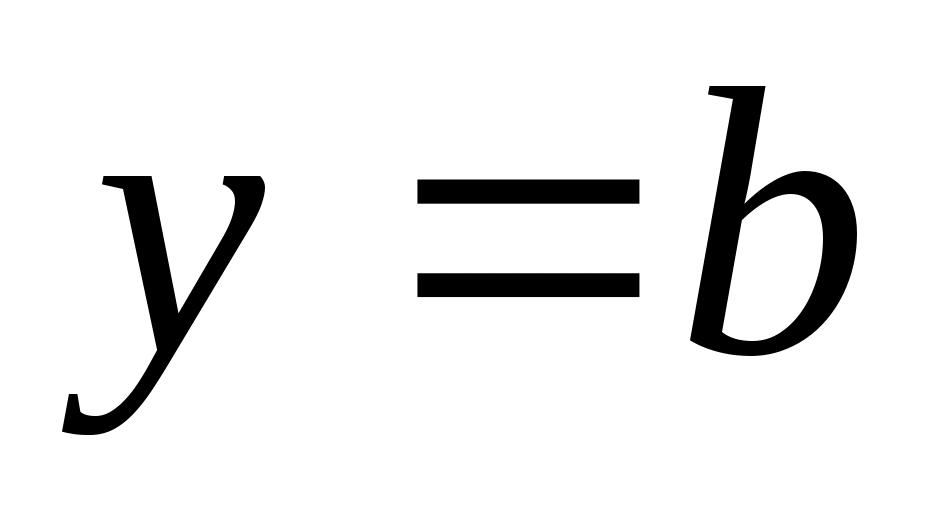 и уравнение (3.1) представляет собой прямую, параллельную оси
и уравнение (3.1) представляет собой прямую, параллельную оси 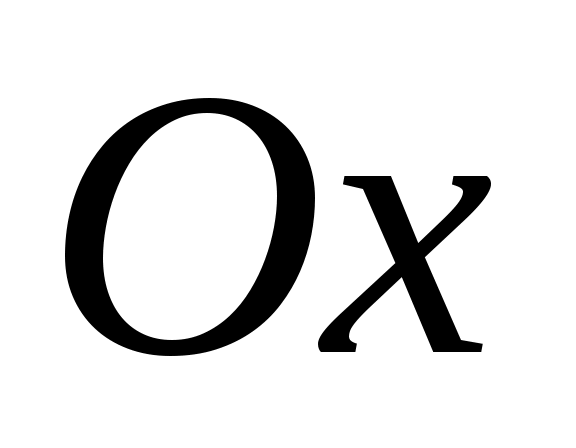 (рис. 3.9).
(рис. 3.9).

-
Если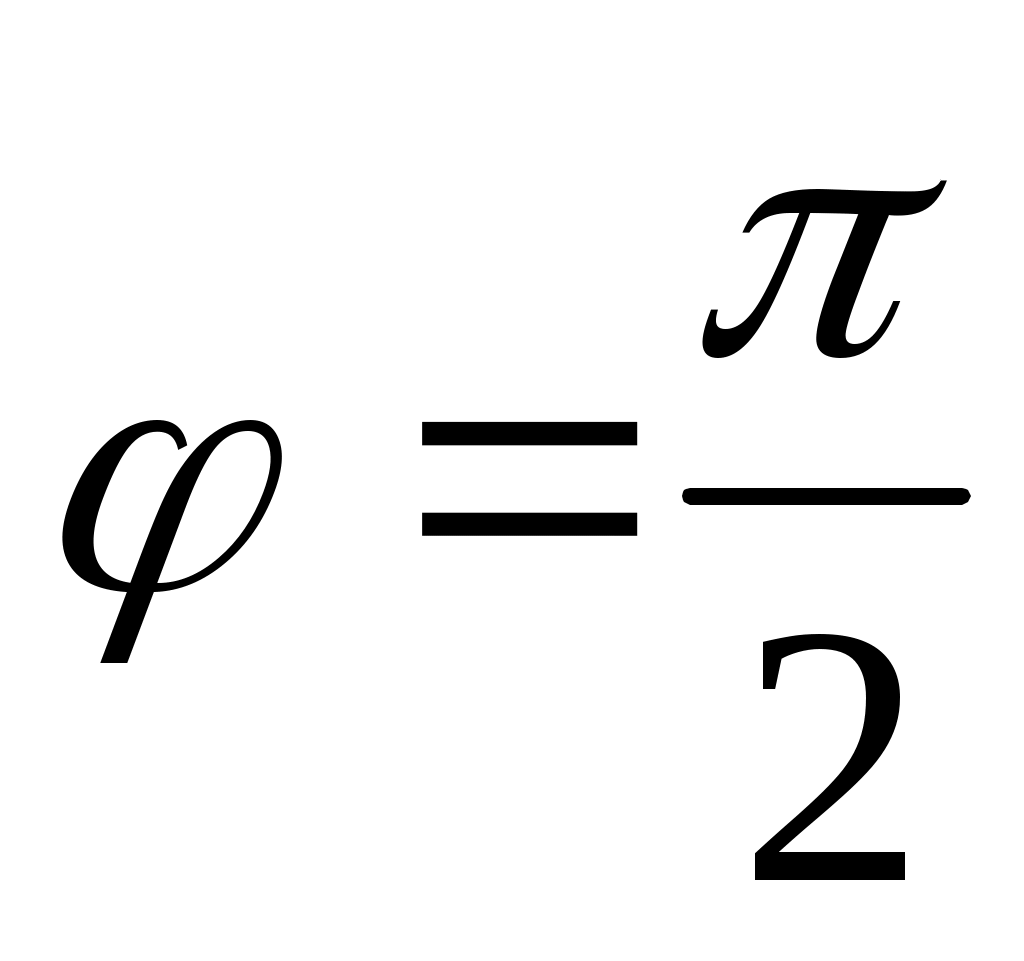 , тогда прямая
, тогда прямая 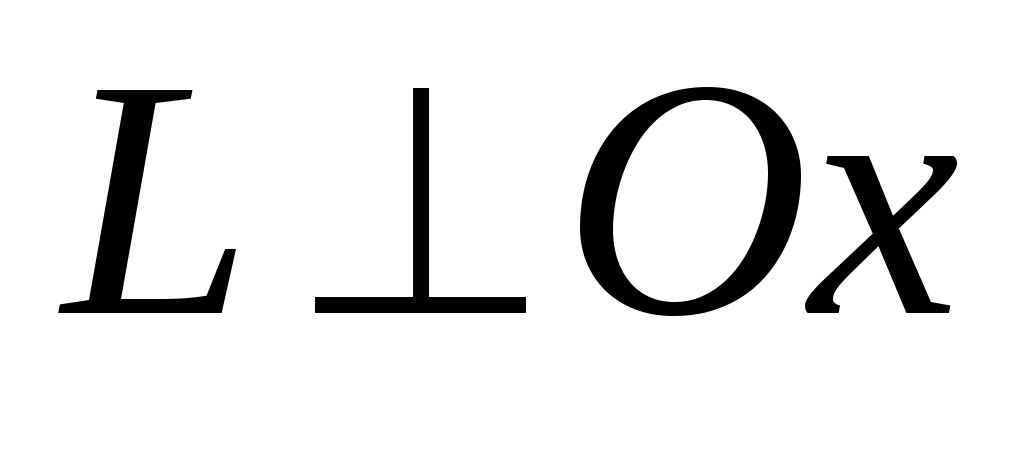 (рис. 3.10). Предположим, что
(рис. 3.10). Предположим, что 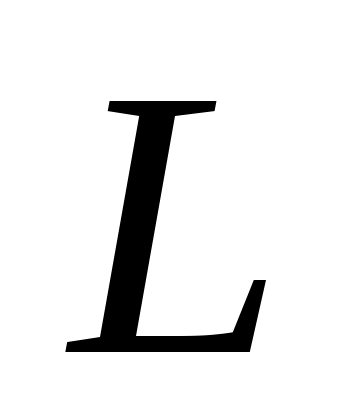 отсекает на оси
отсекает на оси 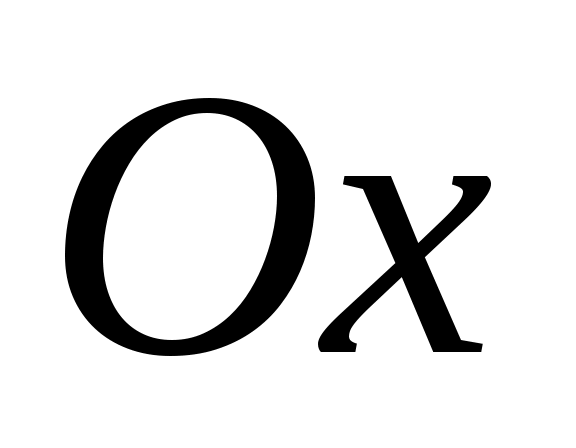 отрезок, равный
отрезок, равный  (рис. 3.10). Очевидно, что уравнений такой прямой
(рис. 3.10). Очевидно, что уравнений такой прямой 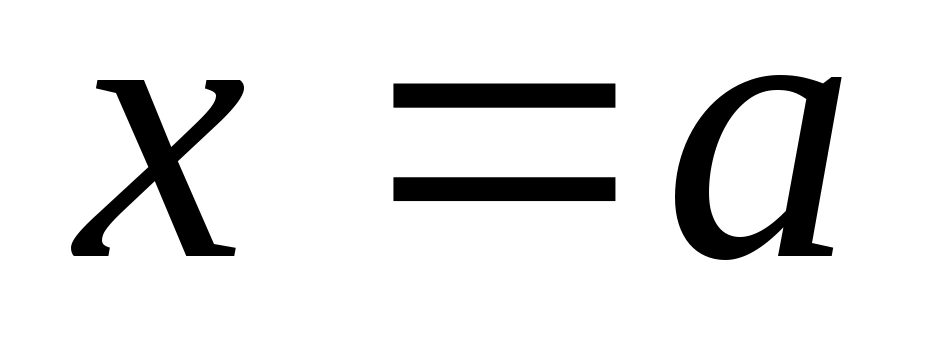 .
.
Уравнение прямой, проходящей через заданную точку в данном направлении
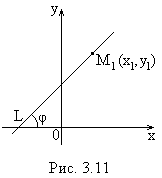 | Пусть прямая Вычитая из (3.1) уравнение (3.2), получим Полученное уравнение называется уравнением прямой по точке и угловому коэффициенту |
Уравнение прямой, проходящей через две заданные точки
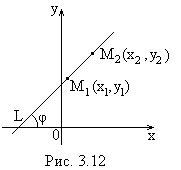 | Пусть известны две точки, принадлежащие Т.к. точка |
Из последнего равенства
Уравнение пучка прямых
Уравнение прямой в отрезках
Уравнение называется уравнением прямой в отрезках.
Общее уравнение прямой и его исследование
Рассмотрим уравнение прямой с угловым коэффициентом
общее уравнение прямой, где и не равны нулю одновременно, т.е.
Рассмотрим частные случаи уравнения (3.6).
-
Если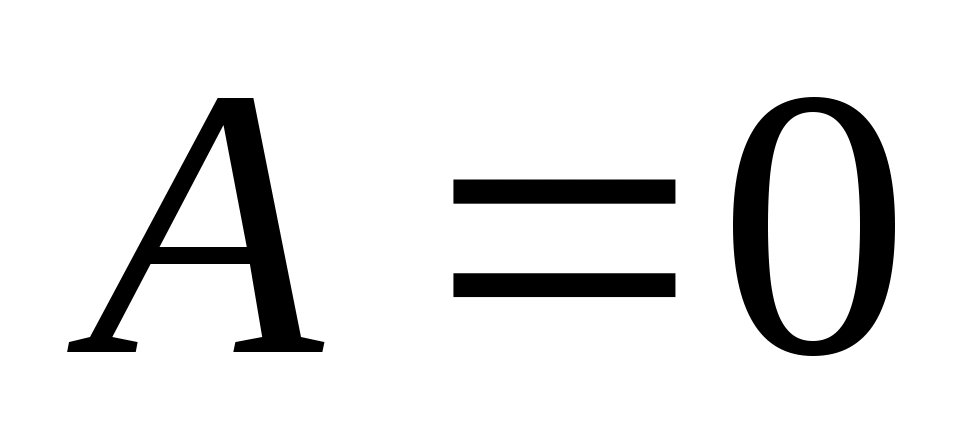 , т.е. уравнение (3.6) не содержит
, т.е. уравнение (3.6) не содержит 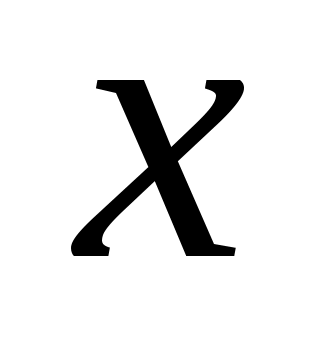 , то оно представляет прямую, параллельную оси
, то оно представляет прямую, параллельную оси 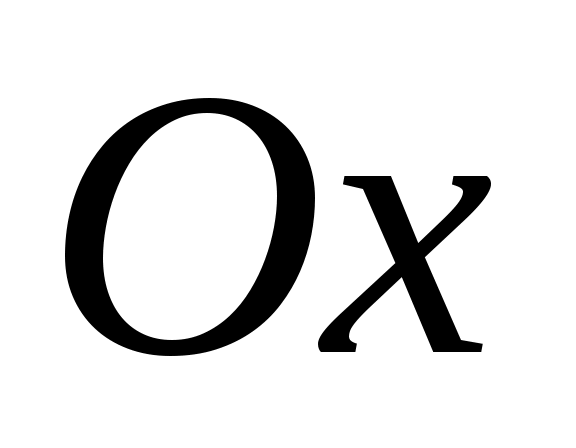 (рис. 3.9):
(рис. 3.9):
Если
-
Если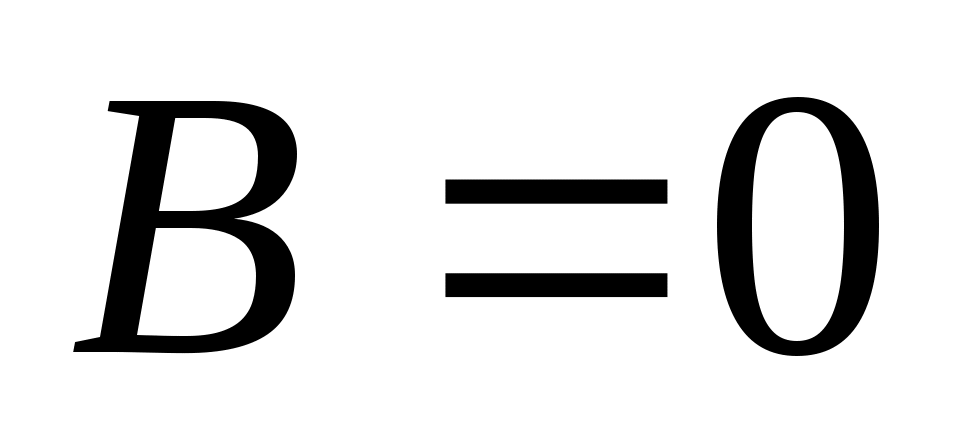 (уравнение не содержит ), тогда прямая параллельна оси
(уравнение не содержит ), тогда прямая параллельна оси 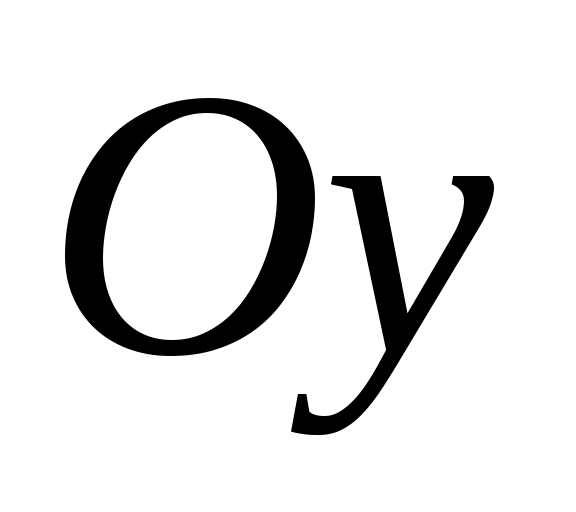 (рис.3.10):
(рис.3.10):
Если
3) Если
Точка пересечения прямых
Если заданы две прямые
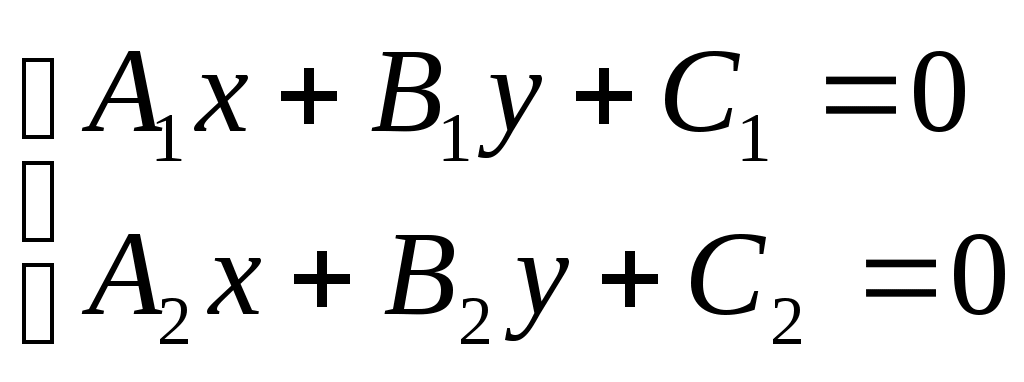 .
.Если прямые не параллельны, т.е.


