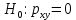
Альтернативная гипотеза:



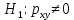
Для проверки гипотезы рассчитываем значение t-критерия Стьюдента:



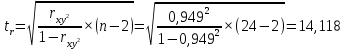
По таблице значений критерия Стьюдента находим табличное (критическое) значение критерия на уровне значимости 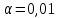(доверительная вероятность 99%) и с числом степеней свободы :



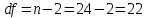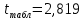
Вывод: поскольку 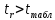, то нулевую гипотезу о равенстве нулю коэффициента корреляции отклоняем с вероятностью допустить ошибку в 1%. С вероятностью 99% связь между признаками является статистически значимой, не случайной.

3. Рассчитаем коэффициенты линейного уравнения регрессии для зависимости потребительских расходов в среднем на душу населения от среднедушевых денежных доходов населения.

Общий вид линейного уравнения парной регрессии:

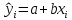, где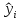

– расчетные теоретические значения результативного признака для 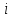-го наблюдения;

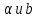– оценки параметров линейного уравнения парной регрессии;

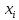– значение факторного признака 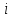-го наблюдения.

Параметры линейного уравнения найдем с помощью метода наименьших квадратов (МНК).

Для определения параметров необходимо решить систему линейных уравнений (систему нормальных уравнений):



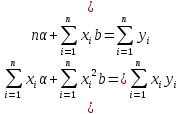
Для расчета параметров можно использовать готовые формулы, которые вытекают из данной системы:





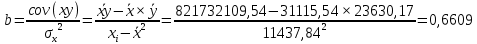
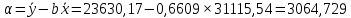
Получили линейное уравнение парной регрессии:

---

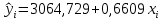
Вывод: коэффициент регрессии 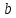показывает, что при увеличении среднедушевых денежных доходов населения 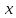на 1 руб., величина потребительских расходов в среднем на душу населения 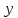в среднем возрастает на 0,6609 руб. Положительное значение подтверждает вывод о прямой зависимости между потребительскими расходами в среднем на душу населения и среднедушевыми денежными доходами населения в месяц.

Свободный член 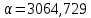оценивает влияние прочих факторов, оказывающих воздействие на результативный признак. Т.е. воздействие прочих факторов уменьшает значение потребительских расходов в среднем на душу населения.

Теоретические (расчетные) значения результативного признака (потребительских расходов на душу населения) 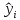получаем путем последовательной подстановки значений факторного признака (среднедушевые денежные доходы населения) 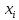в уравнение регрессии.

Рассчитываем остатки, как разность фактических и расчетных значений результативного признака: 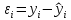. Расчет представлен в таблице 2.

Таблица 2 – Вспомогательная таблица для оценки качества модели

№
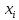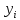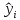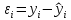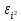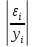1	22797	18052	18132,13	-80,13	6420,82	0,004
2	20334	16133	16504,24	-371,24	137819,14	0,022
3	36735	31757	27344,28	4412,72	19472097,8	0,161
4	46124	32422	33549,82	-1127,82	1271977,95	0,034
5	24386	18237	19182,36	-945,36	893705,53	0,049
6	19503	13484	15951	-2471	6105841	0,155
7	15603	9878	13377,34	-3499,34	12245380,4	0,261
8	21571	18855	17321,18	1533,18	2350640,91	0,088
9	22829	17258	18153,28	-895,28	801526,28	0,049
10	30015	23115	22902,78	212,22	45037,33	0,009
11	24434	17855	19214,08	-1359,08	1847098,45	0,071
12	23166	17749	18376,01	-627,01	393141,54	0,034
13	28852	22895	22134,106	760,89	578953,59	0,034
14	25431	20844	19873,04	970,96	942763,32	0,049
15	27296	20314	21105,69	-791,69	626773,06	0,037
16	24081	20681	18980,77	1700,23	2890782,05	0,089
17	42669	32080	31266,28	813,72	662140,24	0,026
18	23992	18352	18921,95	-569,95	324843,0	0,030
19	48758	33201	35290,73	-2089,73	4366971,47	0,059
20	34619	27638	25945,73	1692,26	2863743,91	0,065
21	39084	32997	28896,82	4100,18	16811476	0,142
22	30937	24938	23512,16	1425,84	2033019,71	0,061
23	59774	35242	42571,62	-7329,62	53723402,6	0,172
24	53783	43147	38611,95	4535,05	20566678,5	0,117
Итого	746773	567124	567119,346	0,00	151962234,6	1,818

---

4. Дадим интервальные оценки для параметров модели парной регрессии с доверительной вероятностью .

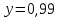Находим остаточную сумму квадратов отклонений:



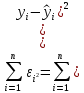
Рассчитываем среднюю квадратическую ошибку модели:



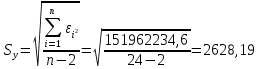
Находим стандартную ошибку свободного члена :



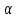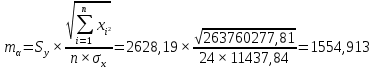
Находим стандартную ошибку коэффициента регрессии :



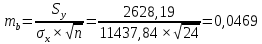
По таблице значений критерия Стьюдента находим табличное (критическое) значение критерия на уровне значимости 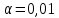и с числом степеней свободы .



Доверительный интервал для свободного члена :







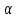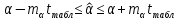
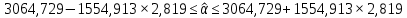
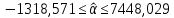
Вывод: c вероятностью 99% значение свободного члена 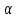будет находится в пределах от 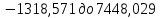. Т.к. в доверительный интервал попадает 0, то свободный член не является статистически значимым.

Доверительный интервал для коэффициента регрессии :







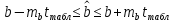
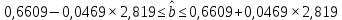
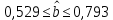
Вывод: с вероятностью 99% значение коэффициента регрессии будет находится в пределах от 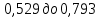. Т.е. с вероятностью 99% при увеличении среднедушевых денежных доходов населения в месяц

---

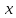на 1 руб. значение потребительских расходов в среднем на душу населения 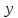возрастет не менее, чем на 0,529 руб., но не более чем на 0,793 руб. Т.к. в доверительный интервал не попадет 0, то коэффициент регрессии является статистически значимым.

5. Проверим статистическую значимость параметров уравнения парной регрессии с надежностью

Выдвигаем нулевые гипотезы о том, что найденные параметры не являются статистически значимым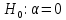и:

и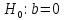

Для проверки гипотез рассчитываем t-критерий Стьюдента:





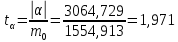
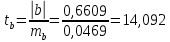
Вывод: поскольку 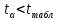, то нулевую гипотезу о равенстве нулю свободного члена 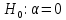принимаем. На уровне значимости 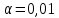свободный член не является статистически значимым, значение показателя случайно. Свободный член признается равным нулю.

Т.к. 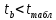, то нулевую гипотезу 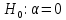отклоняем с вероятностью допустить ошибку в 1%. Коэффициент регрессии является статистически значимым, следовательно, и фактор (среднедушевые денежные доходы населения в месяц) при этом коэффициент не значим.

6. Проверим качество построенного уравнения регрессии

Коэффициент детерминации характеризует долю вариации результативного признака под влиянием фактора, включенного в модель.



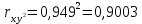
Вывод: 90,03 вариации потребительских расходов в среднем на душу населения 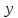происходит под влиянием величины среднедушевых денежных доходов населения в месяц 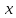. Остальные 9,97% вариации потребительских расходов в среднем на душу населения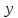

---

объясняется влиянием прочих случайных факторов.

Выдвигаем нулевую гипотезу о том, что найденные показатели тесноты связи случайны, т.е. коэффициент детерминации равен нулю:



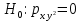
Альтернативная гипотеза:



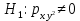
Для проверки нулевой гипотезы рассчитываем значение F-критерия Фишера:



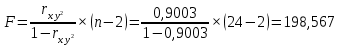
По таблице значений критерия Фишера находим табличное (критическое) значение критерия на уровне значимости 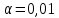и с числом степеней свободы :



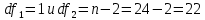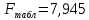
Вывод: поскольку 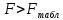, то нулевую гипотезу о равенстве нулю коэффициента детерминации отклоняем с вероятностью допустить ошибку в 1%. Модель зависимости потребительских расходов в среднем на душу населения от среднедушевых денежных доходов населения является статистически значимой, показатели силы связи не случайны.

Для оценки точности модели рассчитываем среднюю относительную ошибку аппроксимации:



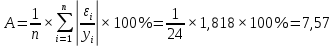
Вывод: средняя относительная ошибка аппроксимации показывает, что в среднем фактические значения потребительских расходов в среднем на душу населения отличаются от полученных по модели на 7,57%. Поскольку ошибка больше 7%, то данное уравнение не желательно использовать в качестве регрессии.

7. Дадим прогноз потребительских расходов в среднем на душу населения с надежностью для гипотетического региона, в котором среднедушевые денежные доходы населения в месяц на 3% больше среднего по выборке.

Прогнозное значение факторного признака:



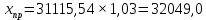
Прогнозное значение результативного признака (точный прогноз):



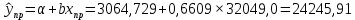
Рассчитываем среднюю квадратическую ошибку прогноза:



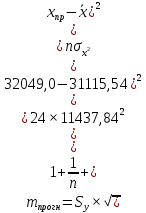
Табличное (критическое) значение критерия на уровне значимости

---

Смотрите также файлы

• И. Ф. Буш выделил один час в неделю для специальных занятий по обучению студентов наложению бандажей и повязок.docx

• Виды кредитных организаций.doc

• После касания униформы, включая головной убор, маску.docx

• Программалы амтамасыз етуді тадау Оу бадарламасына сйкес оыту масаттары.docx

• Классификация наследственных заболеваний человека хромосомные болезни человека.doc