Файл: Лекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика.doc

1. 
   Режимы движения механизма
   

Полное время движения механизма – отрезок времени от момента начала движения до его полной остановки (для механизма с одной степенью свободы – от начала движения до полной остановки начального звена).
На рис.7.1 представлена тахограмма ¹ движения механизма, с начальным звеном в виде кривошипа.


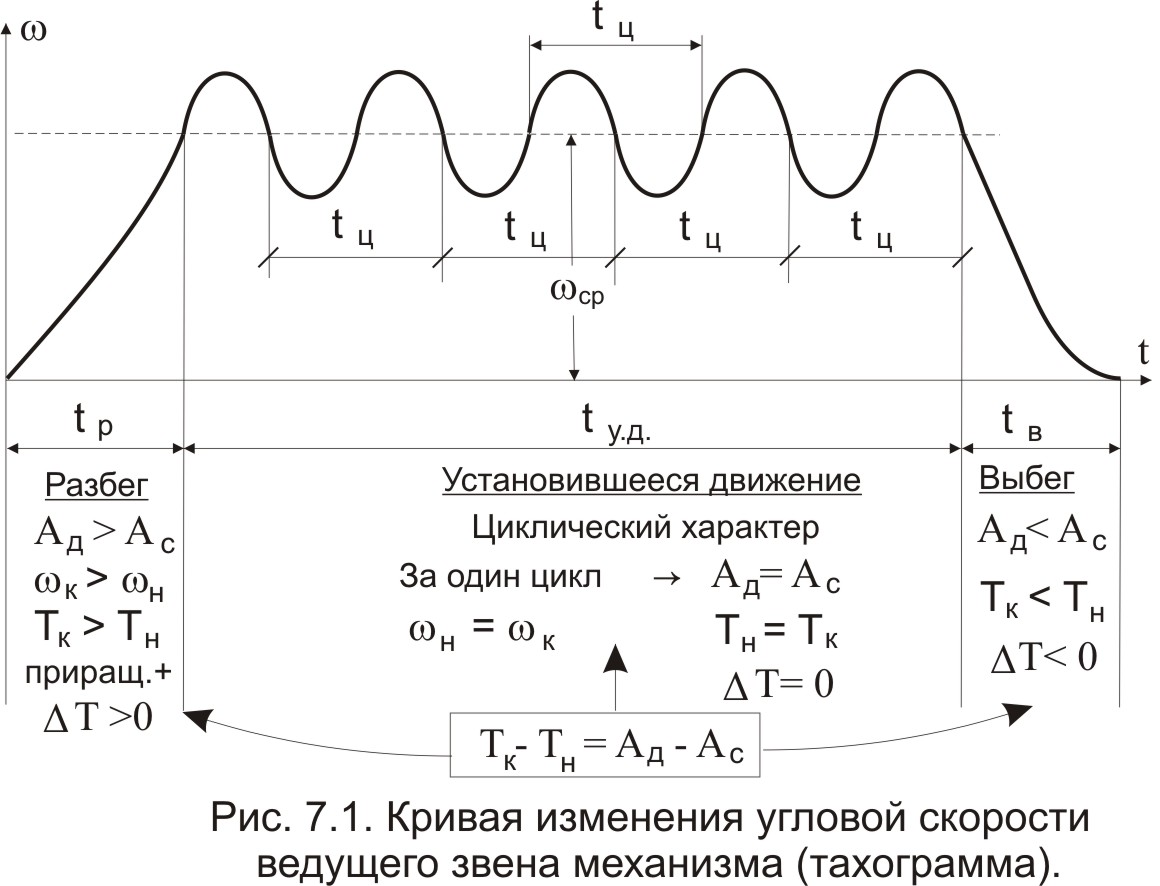
Из графика видно, что в общем случае полное время движения можно разделить на три части:

1. 
   Время разбега – характеризуется увеличением скорости начального звена от нуля до некоторого среднего (номинального) значения рабочей скорости.
   
2. 
   Время установившегося движения – характеризуется периодическим изменением скорости начального звена около среднего значения рабочей скорости. При этом все кинематические характеристики начального звена (положение кривошипа, его угловая скорость, угловое ускорение) - периодические функции. Кинетическая энергия механизма во времени изменяется также по периодическому закону. Промежуток времени, по истечении которого положение начального звена, его скорость и ускорение, а также кинетическая энергия механизма принимают первоначальные значения и затем начинают периодически повторяться – называют циклом установившегося движения.
   
3. 
   Время выбега – характеризуется убыванием скорости начального звена от средней рабочей скорости до полной остановки.
   

На диаграмме (Рис.7.1) использованы следующие обозначения:

- работа движущих сил и работа сил сопротивления за один полный цикл;

- угловая скорость начального звена вначале цикла и в конце цикла;

- кинетическая энергия механизма вначале цикла и в конце цикла;

- время разбега, время установившегося движения, время выбега;

- время цикла установившегося движения.
В рамке под диаграммой приведено выражение теоремы об изменении кинетической энергии механизма для времени полного цикла (интегральная форма теоремы). Из теоремы следует, что при

---

> приращение кинетической энергии механизма за цикл положительно, т.е. угловая скорость начального звена увеличивается. И, наоборот, при < приращение кинетической энергии за цикл отрицательно, что соответствует уменьшению угловой скорости начального звена. Наконец, при = приращение кинетической энергии за один цикл равно нулю, а, значит, скорости начального звена вначале и в конце цикла одинаковы.

2. 
   Неравномерность движения начального звена. Средняя скорость. Коэффициент неравномерности
   

Часто на вопрос о характеристиках движения механизма в установившемся режиме работы студенты отвечают: «Это режим работы, при котором все показатели выходят на номинальный рабочий уровень, т.е. стабилизируются».

Это неверный ответ.

Из предыдущего параграфа (п.7.1) следует, что угловая скорость начального звена в установившемся режиме изменяется, т.е. движение начального звена является неравномерным.

В чем же причина такой неравномерности?

Для анализа этого явления решим уравнение (6.29) относительно углового ускорения:

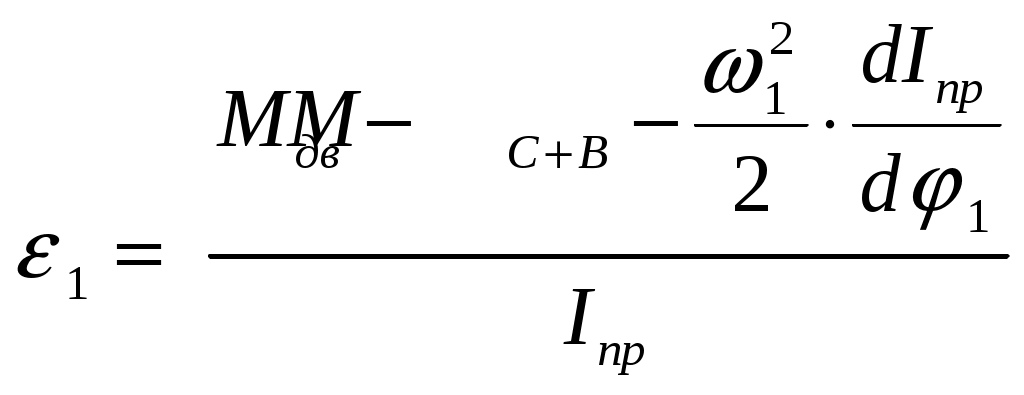, (7.1)
Из (7.1) видно, что угловое ускорение зависит от ряда факторов. Движение будет равномерным, если обеспечить . Возможно ли это на практике?

Из трех составляющих числителя (7.1) только движущий момент (момент на валу кривошипа) условно можно считать постоянным ¹ и не зависящим от положения начального звена, т.е. .

---

Приведенный момент сил сопротивления и веса зависит от закона изменения сил полезных и вредных сопротивлений, а также от величины и направления скоростей точек приложения этих сил и сил веса звеньев. Величина этого момента может быть установлена расчетным путем. Известно, что она может изменяться по весьма сложному закону и в весьма широких пределах. Таким образом, ≠ .

Третья составляющая содержит приведенный момент инерции механизма , который является функцией и зависит от кинетической энергии звеньев. Сама кинетическая энергия может изменяться от нуля (при полной остановке отдельных звеньев) до некоторого максимального значения. Отсюда следует, что для рычажных механизмов .
Обобщив результаты анализа, приходим к выводу, что неравномерность движения начального звена для рычажных механизмов - явление не просто возможное, а скорее – обычное и закономерное.

Причинами неравномерности следует считать:

1. 
   изменение сил сопротивления при движении механизма (смотри, например, график сил трения в поступательной паре ползун-стойка в курсовом проекте);
   
2. 
   различное влияние сил тяжести звеньев (при опускании центров масс звеньев, силы тяжести являются движущими силами и, наоборот, при их подъеме – силами сопротивления);
   
3. 
   сложный характер изменения приведенного момента инерции механизма (что означает изменение величины и направления сил инерции звеньев).
   

Неравномерность движения количественно оценивается по величине коэффициента неравномерности ( ). Коэффициент вычисляется, исключительно, для режима установившегося движения.

---

Д 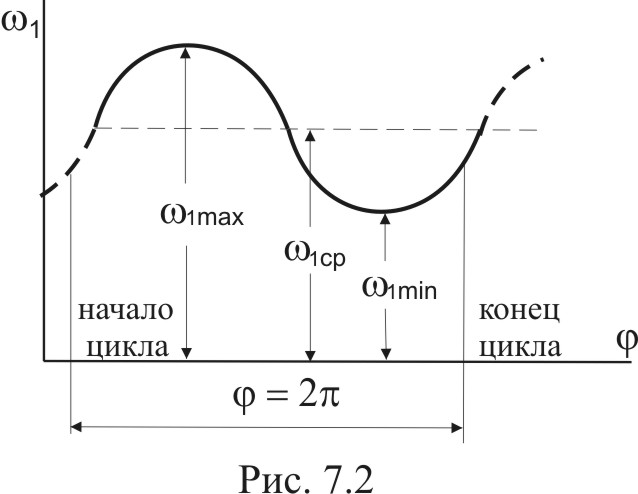ля вывода расчетной формулы введем понятия максимальной, минимальной и средней скорости начального звена.

Рассмотрим изменение угловой скорости начального звена за один цикл установившегося движения (Рис.7.2). Наибольшую скорость в цикле будем считать максимальной (_1max), а наименьшую – минимальной (_1min). Среднюю угловую скорость звена найдем приближенно, как полу-сумму _1max и _1min : ¹
(7.2)

Коэффициент неравномерности численно определяется отношением амплитуды изменения угловой скорости (_1max - _1min) к величине средней скорости _1ср, т.е.:
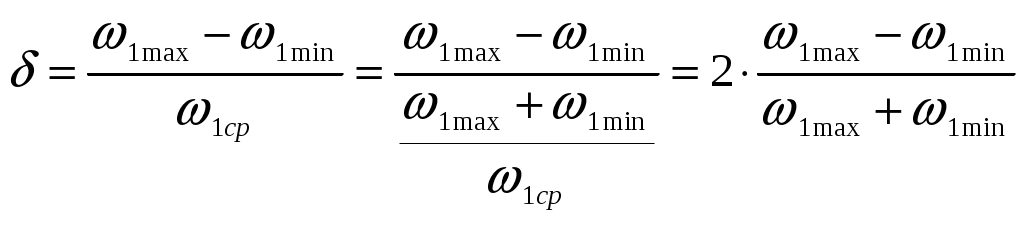(7.3)
Теоретические пределы изменения .
Нижний предел (т.е. = 0) комментариев не требует. Действительно, при условии _1max - _1min = 0 выражение (7.3) дает такой результат. Это режим равномерного движения начального звена механизма, когда _1max = _1min = _1ср. Как показано ранее, этот режим для реальных механизмов является недостижимым идеалом.

Второй предел (т.е. = +) трудно объяснить, опираясь на выражение (7.3). Даже если предположить, что _1min = 0 (это случай максимально большой амплитуды ₁ ) из (7.3) получаем в результате = 2. Парадокс объясняется тем, что истинное значение средней скорости отличается от вычисленного по (7.2) приближенного значения. Так, например, при кратковременном движении с _1max и длительной остановке с _1min = 0 истинная средняя скорость _1ср будет стремиться к нулевому значению (_1ср  0). Подставив в (7.3) _1ср = 0, получим правильный результат

---

= +.
Неравномерность движения для механизмов и машин - явление нежелательное. Она ведет к появлению целого ряда негативных факторов. Так, возникающие при изменении скорости ведущего звена дополнительные ускорения всех звеньев вызывают добавочные динамические нагрузки в кинематических парах и элементах привода механизма. Кроме того, в связи с неравномерностью могут возникать дополнительные колебания звеньев, отрицательно влияющие на динамику и ресурс работы машины. В силу этих причин, от неравномерности стремятся если не избавиться полностью, то хотя бы уменьшить. Одно из решений в данном случае – установка маховика (см. Лекции по ТММ, Часть 2, Лекция 8).

Значения для некоторых реальных типов машин приведены ниже:

1. 
   Насосы, сельскохозяйственные машины, конвейеры . . . . . . . . . 0,20,1
   
2. 
   Металлообрабатывающие станки, двигатели внутреннего
   

сгорания (ДВС) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 0,020,01

3. 
   Электродвигатели, генераторы . . . . . . . . . . . . . . . . . . . . . . . . . 0,010,005
   
4. 
   Авиационные двигатели, турбогенераторы . . . . . . . . . . . . меньше 0,005
   

Из таблицы видно, что более быстроходным машинам соответствуют меньшие значения коэффициента . И, напротив, для тихоходных машин требования к равномерности движения менее жесткие.

3. 
   Диаграмма “Энергия - масса” при установившемся режиме работы. Порядок построения.
   

Диаграмма “Энергия - масса” (диаграмма Виттенбауэра) – графическая зависимость приращения кинетической энергии механизма ( Δ ) от приведенного момента инерции ( Δ ).
Диаграмма может быть использована:

• 
  для определения коэффициента неравномерности механизма;
  
• 
  для подбора маховика с целью снижения ;
  
• 
  для определения текущего значения угловой скорости начального звена ₁.
  

Построение диаграммы выполняется в несколько этапов:

---