Файл: Выделить и формально описать наиболее существенные связи экономических объектов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 46
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
х 0 означает, что обе компоненты вектора х = (х1 , х2 ) строго положительны.
4. х 0 2 f / x2i 0, i = 1, 2.
Свойство 4 (вторая производная производственной функции по любой координате неположительна) означает, что с ростом объема затрат одного из ресурсов при неизменном объеме использования другого ресурса величина прироста выпуска на каждую дополнительную единицу i-го ресурса не увеличивается (это свойство известно как закон убывающей эффективности).
5. При х 0 2 f / ( xi x2 ) 0.
Это свойство означает, что с ростом затрат одного из ресурсов предельная эффективность другого ресурса возрастает.
6. f ( tx1 , tx2 ) = t p f ( x1 , x2 ).
Свойство 6 означает, что производственная функция является однородной функцией степени р. Иными словами, при переходе от вектора затрат ресурсов х к вектору tх объем выпуска изменяется в t p раз. При р 1 имеем рост выпуска в t p раз с ростом масштаба производства в t раз; при р 1 имеем снижение выпуска в t p раз с ростом масштаба производства в t раз. При р = 1 имеем постоянную эффективность производства независимо от роста его масштаба.
Средние и предельные значения производственной функции
Рассмотрим многофакторную производственную функцию (5)
y = f (x ) = f (x1 , x2 ,…,xn ).
1. Средней производительностью i-го ресурса, или средним выпуском по i-му ресурсу, называется величина
Ai = f (x ) / xi , i = 1, 2, … , n. (15)
2. Предельной (маржинальной) производительностьюi-го ресурса, или предельным выпуском по i-му ресурсу, называется первая частная производная
Mi = f / xi , i = 1, 2, … , n. (16)
в приращениях функции и аргумента частную производную можно приближенно представить в виде
Mi
i f (x ) xi , i = 1, 2, … , n.
3. Отношение предельной производительности i-го ресурса к его средней производительности
Ei = Mi / Ai = ( xi / f (x )) ( f / xi ) , , i = 1, 2, … , n. (17)
Называется эластичностью выпуска по i-му ресурсу (частной эластичночтью выпуска). В экономической теории для эластичности часто используется разностный аналог формулы (17):
Ei = ( f / f 100% ) / ( xi / xi 100% ).
Из этой формулы следует, что эластичность выпуска по i-му ресурсу равна относительному изменению объема выпуска при изменении затрат этого ресурса на один процент.
Сумма всех эластичностей
Ех = Е1 + Е2 + … + Еп
называетсяэластичностью производства.
Средние и маржинальные показатели, а также эластичность производственной функции являются одними из основных характеристик, используемых в экономике.
Пример 2.
Найдем средние и маржинальные значения, а также эластичности для двухфакторных мультипликативной и аддитивной функции.
Решение.
а) Для мультипликативной ПФ типа Кобба-Дугласа (10) имеем:
A1 = f (x ) / x1 = a0 x1a1 - 1 x2a2 , A2 = f (x ) / x2 = a0 x1a1 x2a2 - 1
M1 = f / x1 = a1 A1 , M2 = f / x2 = a2 A2
E1 = M1 / A1 =a1 , E2 M2 / A2 = a2 .
Из полученных выражений с учетом соотношений (14) следует, что
Mi Ai , i = 1, 2 ,
б) Для аддитивной функции вида (9) имеем:
A1 = f (x ) / x1 = a0 / x1 + a1 + a2 x2 / x1 ,
A2 = f (x ) / x2 = a0 / x2 + a2 + a1 x1 / x2
M1 = f / x1 = a1 , M2 = f / x2 = a2
E1 = M1 / A1 =a1 / (a0 / x1
+ a1 + a2 x2 / x1 ) ,
E2 M2 / A2 = a2 / (a0 / x2 + a2 + a1 x1 / x2 ) .
Величина
Rij = -dxj / dxi ( i, j = 1, 2 ) (18)
В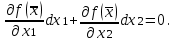
ыражение для Rij. Поскольку f (x ) = const, то df = 0, т.е. первый дифференциал равен нулю, откуда следует:
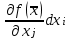
П
оделив это уравнение на ( i, j = 1, 2 ) , получаем выражение для предельной нормы замены i-го ресурса j-м ресурсом:
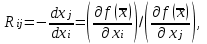

( i j, i, j = 1, 2 ). (19)
Для двухфакторной производственной функции справедливо равенство
Rij = ( E1 x2 ) / ( E2 x1 ) , (20)
Что непосредственно проверяется прямой подстановкой выражений для эластичности (17) в соотношение (19).
Пример 3.
Найдем выражения для предельных норм замены в случаях: а) производственнойфункции Кобба-Дугласа (13) и б) аддитивной двухфакторной ПФ (9).
Решение.
а) Подставляя в формулу (20) выражения эластичности для мультипликативной функции (см. пример 2а), получаем:
R12 = ( 1L ) / ( 2K ), R21 = ( 2 K ) / ( 1 L ).
Б) Аналогичная подстановка в случае аддитивной ПФ (пример 2б) приводит к еще более простым выражениям:
R12 = a1 /a2 , R21 = a2 / a1 .
Убывающая эффективность производства
Рассмотрим производственную функцию Кобба-Дугласа. Поделив обе части уравнения (13) на переменную L, получаем с учетом равенства 1 +
2 = 1 однофакторную производственную функцию:
y = a0 ka1 , (21)
где y = Y / L – производительность труда, k = K / L – фондовооруженность. График функции (21) показан на рис. 1.
Поскольку 1 1, то вторая производная
d2 y / d k2 = a01 ( 1 – 1 ) k1 – 1 0 ,
Пример 4.
Выпуск однопродуктовой фирмы определяется ПФ Кобба-Дугласа Y=3K1/3L2/3. Найти распределение фондов К и затрат труда L, при котором выпуск будет максимальным, если на аренду фондов и оплату труда выделено 150 денежных единиц (д.е.), стоимость аренды фондов wL=5 д.е./чел.
Решение.
пусть К и L - искомые распределение фондов и затраты труда, тогда по условию задачи имеем KwK+LwL=150. Из этого уравнения связи выразим одно искомое неизвестное через другое, например L через K:L=150/wL-KwK/wL=30-2K. Далее подставляем полученное выражение в уравнение производственной функции, откуда получаем функцию одной переменной – аргумента KY=3K1/3(30-2K)2/3. Теперь находим точку максимума этой функции, приравнивая нулю производную:
Y = (30-2K)2/3 / K2/3 – 4K1/3 / (30-2K)1/3 = 0.
Отсюда последовательно получаем, что К = 5 е.ф., L = 20 чел.
Рис. 1
 Y
Y


 y
y


y


4. х 0 2 f / x2i 0, i = 1, 2.
Свойство 4 (вторая производная производственной функции по любой координате неположительна) означает, что с ростом объема затрат одного из ресурсов при неизменном объеме использования другого ресурса величина прироста выпуска на каждую дополнительную единицу i-го ресурса не увеличивается (это свойство известно как закон убывающей эффективности).
5. При х 0 2 f / ( xi x2 ) 0.
Это свойство означает, что с ростом затрат одного из ресурсов предельная эффективность другого ресурса возрастает.
6. f ( tx1 , tx2 ) = t p f ( x1 , x2 ).
Свойство 6 означает, что производственная функция является однородной функцией степени р. Иными словами, при переходе от вектора затрат ресурсов х к вектору tх объем выпуска изменяется в t p раз. При р 1 имеем рост выпуска в t p раз с ростом масштаба производства в t раз; при р 1 имеем снижение выпуска в t p раз с ростом масштаба производства в t раз. При р = 1 имеем постоянную эффективность производства независимо от роста его масштаба.
Средние и предельные значения производственной функции
Рассмотрим многофакторную производственную функцию (5)
y = f (x ) = f (x1 , x2 ,…,xn ).
1. Средней производительностью i-го ресурса, или средним выпуском по i-му ресурсу, называется величина
Ai = f (x ) / xi , i = 1, 2, … , n. (15)
2. Предельной (маржинальной) производительностьюi-го ресурса, или предельным выпуском по i-му ресурсу, называется первая частная производная
Mi = f / xi , i = 1, 2, … , n. (16)
в приращениях функции и аргумента частную производную можно приближенно представить в виде
Mi
i f (x ) xi , i = 1, 2, … , n.
3. Отношение предельной производительности i-го ресурса к его средней производительности
Ei = Mi / Ai = ( xi / f (x )) ( f / xi ) , , i = 1, 2, … , n. (17)
Называется эластичностью выпуска по i-му ресурсу (частной эластичночтью выпуска). В экономической теории для эластичности часто используется разностный аналог формулы (17):
Ei = ( f / f 100% ) / ( xi / xi 100% ).
Из этой формулы следует, что эластичность выпуска по i-му ресурсу равна относительному изменению объема выпуска при изменении затрат этого ресурса на один процент.
Сумма всех эластичностей
Ех = Е1 + Е2 + … + Еп
называетсяэластичностью производства.
Средние и маржинальные показатели, а также эластичность производственной функции являются одними из основных характеристик, используемых в экономике.
Пример 2.
Найдем средние и маржинальные значения, а также эластичности для двухфакторных мультипликативной и аддитивной функции.
Решение.
а) Для мультипликативной ПФ типа Кобба-Дугласа (10) имеем:
A1 = f (x ) / x1 = a0 x1a1 - 1 x2a2 , A2 = f (x ) / x2 = a0 x1a1 x2a2 - 1
M1 = f / x1 = a1 A1 , M2 = f / x2 = a2 A2
E1 = M1 / A1 =a1 , E2 M2 / A2 = a2 .
Из полученных выражений с учетом соотношений (14) следует, что
Mi Ai , i = 1, 2 ,
б) Для аддитивной функции вида (9) имеем:
A1 = f (x ) / x1 = a0 / x1 + a1 + a2 x2 / x1 ,
A2 = f (x ) / x2 = a0 / x2 + a2 + a1 x1 / x2
M1 = f / x1 = a1 , M2 = f / x2 = a2
E1 = M1 / A1 =a1 / (a0 / x1
+ a1 + a2 x2 / x1 ) ,
E2 M2 / A2 = a2 / (a0 / x2 + a2 + a1 x1 / x2 ) .
Величина
Rij = -dxj / dxi ( i, j = 1, 2 ) (18)
В
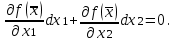
ыражение для Rij. Поскольку f (x ) = const, то df = 0, т.е. первый дифференциал равен нулю, откуда следует:
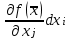
П

оделив это уравнение на ( i, j = 1, 2 ) , получаем выражение для предельной нормы замены i-го ресурса j-м ресурсом:
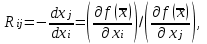

( i j, i, j = 1, 2 ). (19)
Для двухфакторной производственной функции справедливо равенство
Rij = ( E1 x2 ) / ( E2 x1 ) , (20)
Что непосредственно проверяется прямой подстановкой выражений для эластичности (17) в соотношение (19).
Пример 3.
Найдем выражения для предельных норм замены в случаях: а) производственнойфункции Кобба-Дугласа (13) и б) аддитивной двухфакторной ПФ (9).
Решение.
а) Подставляя в формулу (20) выражения эластичности для мультипликативной функции (см. пример 2а), получаем:
R12 = ( 1L ) / ( 2K ), R21 = ( 2 K ) / ( 1 L ).
Б) Аналогичная подстановка в случае аддитивной ПФ (пример 2б) приводит к еще более простым выражениям:
R12 = a1 /a2 , R21 = a2 / a1 .
Убывающая эффективность производства
Рассмотрим производственную функцию Кобба-Дугласа. Поделив обе части уравнения (13) на переменную L, получаем с учетом равенства 1 +
2 = 1 однофакторную производственную функцию:
y = a0 ka1 , (21)
где y = Y / L – производительность труда, k = K / L – фондовооруженность. График функции (21) показан на рис. 1.
Поскольку 1 1, то вторая производная
d2 y / d k2 = a01 ( 1 – 1 ) k1 – 1 0 ,
Пример 4.
Выпуск однопродуктовой фирмы определяется ПФ Кобба-Дугласа Y=3K1/3L2/3. Найти распределение фондов К и затрат труда L, при котором выпуск будет максимальным, если на аренду фондов и оплату труда выделено 150 денежных единиц (д.е.), стоимость аренды фондов wL=5 д.е./чел.
Решение.
пусть К и L - искомые распределение фондов и затраты труда, тогда по условию задачи имеем KwK+LwL=150. Из этого уравнения связи выразим одно искомое неизвестное через другое, например L через K:L=150/wL-KwK/wL=30-2K. Далее подставляем полученное выражение в уравнение производственной функции, откуда получаем функцию одной переменной – аргумента KY=3K1/3(30-2K)2/3. Теперь находим точку максимума этой функции, приравнивая нулю производную:
Y = (30-2K)2/3 / K2/3 – 4K1/3 / (30-2K)1/3 = 0.
Отсюда последовательно получаем, что К = 5 е.ф., L = 20 чел.
Рис. 1
 Y
Y 


 y
y

y


