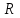Файл: Выделить и формально описать наиболее существенные связи экономических объектов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 49
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Ожидаемая доходность портфеля, состоящего из n ценных бумаг, равна
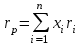
((70)
где xi – доля начальной стоимости портфеля, инвестированная в i-й вид ценных бумаг, ri – ожидаемая доходность i-го вида ценных бумаг, n – количество видов ценных бумаг в портфеле.
Рис. 4
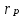
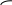
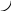
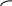
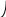
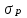
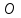
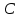
Стандартное отклонение портфеля rp вычисляется следующим образом. Дисперсия доходности портфеля – это дисперсия суммы случайных величин; как известно из теории математической статистики, она равна ковариации :
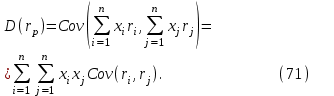
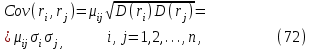
Здесь Cov(ri,rj) – ковариация ожидаемых доходностей ценных бумаг i и j, вычисляемая по формуле
Где
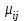- коэффициент корреляции между доходностями 
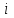-й и 
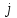-й ценных бумаг, D и 
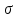- соответственно дисперсия и стандартное (среднее квадратическое отклонение) доходностей ценных бумаг. Как известно,
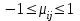.Формула для стандартного отклонения портфеля имеет вид:
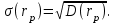(73)Пример 1.
Найти ожидаемую доходность и стандартное отклонение доходности портфеля, состоящего из 30% акций компании А и 70% компании В, если их доходности некоррелированы и равны соответственно 20% и 10%, а стандартные отклонения – 10% и 5%.
Решение.
По формуле (70) получаем:
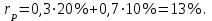Поскольку доходности бумаг некоррелированы , то 
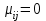при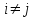 
и тогда 
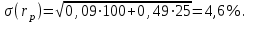
Приведённый пример показывает, что портфель ценных бумаг обладает меньшим риском, чем некоторые отдельные составляющие его бумаги. Это свойство портфеля называется диверсификацией: увеличение количества видов ценных бумаг при одновременном сокращении их долей в общей ожидаемой доходности уменьшает риск портфеля.
Пример 2.
Найти ожидаемую доходность и её стандартное отклонение для портфеля, состоящего из 10 видов ценных бумаг с некоррелированными доходностями. Доли ценных бумаг
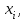их доходности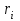 
и стандартные отклонения
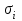приведены в таблице.Таблица 1.
| Пара-метры | Номера ценных бумаг i | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| xi ¸ % | 10 | 10 | 10 | 10 | 10 | 10 | 20 | 10 | 5 | 5 |
| ri ¸ % | 15 | 15 | 18 | 12 | 25 | 20 | 10 | 28 | 35 | 40 |
| σi ¸ % | 8 | 8 | 10 | 7 | 12 | 10 | 5 | 15 | 20 | 25 |
Решение.
rp = 0,1 · 15 + 0,1 · 15 + 0,1 · 18 + 0,1 · 12 + 0,1 · 25 + 0,1 · 20 + 0,2 · 10 + 0,1 · 28 +
+ 0,005 · 35 + 0,005 · 40 = 19,05 %.
Так как случайные величины доходностей бумаг являются независимыми, то дисперсия доходности портфеля равна
D ( rp ) = 0,01 · 64 + 0,01 · 64 + 0,01 · 100 + 0,01 · 49 + 0,01 · 144 + 0,01 · 100 +
+ 0,04 · 25 0,01 · 225 + 0,0025 · 400 + 0,0025 · 625 = 11,02.
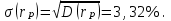
Тогда
На рис. 5 показано достижимое множество, представляющее собой все портфели, которые можно сформировать из n видов ценных бумаг.
Рис. 5
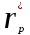
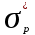
Рис. 6
