Файл: Выделить и формально описать наиболее существенные связи экономических объектов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.05.2024
Просмотров: 50
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

O 1 1 X
МОДЕЛЬ ПОТРЕБИТЕЛЬСКОГО ВЫБОРА
х = ( х1, х2, …, хп ), (22)
Функции полезности
На множестве потребительских наборов Х определена функция
и ( х ) = и ( х1 , х2 , …, хп ) , (23)
Свойства функции полезности в предположении о ее дифференцируемости.
1. u /xi = ui 0, i = 1, 2, …, n. (24)
2. 2 u / x2i = uii < 0, i = 1, 2, …, n, (25)
Предельная полезность любого товара уменьшается с ростом его потребления. Это утверждение называется законом Госсена
3. 2 u / ( xixj ) = uij > 0, i j, ( i, j = 1, 2, …, n ). (26)
Это свойство означает, что предельная полезность каждого продукта увеличивается с ростом количества другого продукта.
Несколько видов функций полезности, удовлетворяющих принятым допущениям.
а) Неоклассическая:
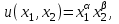 , > 0, + < 1. (27)
, > 0, + < 1. (27)б) Квадратическая:
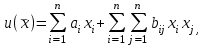 (28)
(28)в) Логарифмическая функция:
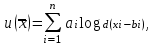 (29)
(29)Линии безразличия
u ( x1 , x2 ) = const . (30)
Основные свойства линий безразличия.
1. Линии безразличия, соответствующие разным уровням удовлетворения потребностей, не касаются и не пересекаются. Это следует из вида их определения (30).
-
Линии безразличия убывают. Рассмотрим уравнение этой линиив виде
x2
= ( x1 ) , (31)
которое можно получить из (30).
d x2 / d x1 = - u1 / u2(32)
3. Линии безразличия выпуклы вниз. Действительно, вторая производная функции (31), согласно правилу дифференцирования частного, вычисляется по формуле:
d ( d x2 / d x1 ) / d x1 = d2 x2 / = - ( u11 u2 - u21 u1 ) / ( u2 )2.
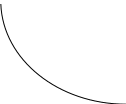
Характерный вид линий безразличия функции полезности показан на рис. 2.
Из формулы (32) следует важное приближенное равенство
-x2 /x1 u1 / u2.
Пример 1.
Если предельная полезность первого товара равна 6, а второго товара – 2, то при уменьшении потребления первого товара на единицу нужно увеличить потребление второго товара на 3 единицы при том же уровне удовлетворения потребностей.

Рис. 2
 Х2
Х2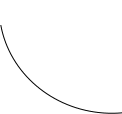
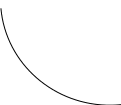 С1
С1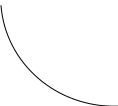
C4
C3
C2
C1

X1
Бюджетное множество
Поскольку граница G определяется соотношением px = I, то бюджетное множество В описывается системой следующих неравенств:

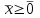 ,
, 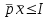 , (33)
, (33)или в развернутой форме:
хi
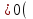 i=1,2,…,n), p1x1+p2x2+…+pnxn
i=1,2,…,n), p1x1+p2x2+…+pnxn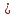 I (34)
I (34)Для случая набора из двух товаров бюджетное множество представляет собой треугольник в системе координат х1Ох2, ограниченный координатными осями и прямой р1х1+р2х2= I (рис.3).
Рис. 3
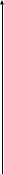
X2


I/p2








 p1x1 + p2x2 = I
p1x1 + p2x2 = I































1 2 3 4
O I/p1 X1
Задача потребительского выбора

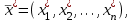 (35)
(35)Формальный вид задачи потребительского выбора – ищется точка максимума (35) функции полезности на бюджетном множестве
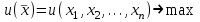 (36)
(36)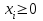
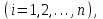
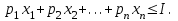
Рассмотрим задачу потребительского выбора для случая набора для двух товаров: найти набор
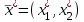 такой что
такой чтоПоиск оптимального набора
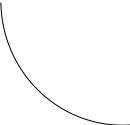
 можно интерпретировать графически как последовательный переход на линии безразличия более высокого уровня полезности (рис.4)- вправо-вверх - до тех пор, пока эти линии имеют общие точки с бюджетным множеством.
можно интерпретировать графически как последовательный переход на линии безразличия более высокого уровня полезности (рис.4)- вправо-вверх - до тех пор, пока эти линии имеют общие точки с бюджетным множеством.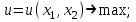
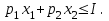 (38)
(38)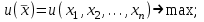 (39)
(39)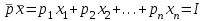 .
.Последнее уравнение в (39) называется уравнением связи.
Рис. 4
Х2

 х
х
2

O x2 X1
Решение задачи потребительского выбора
Функция Лагранжа
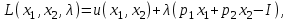 (40)
(40)где - неопределенный множитель Ланранжа. Экономический смысл этого множителя: если цены и доход меняются в одно и то же число раз , то функция полезности, а значит, и решение задачи потребительского выбора не изменится. Далее ищется точка максимума функции L: все три частные производные этой функции приравниваются к нулю, т.е. получаем систему трех уравнений:
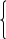 L / х1 = u1 - p1 = 0,
L / х1 = u1 - p1 = 0,L / х2 = u2 - p2 = 0,
L / =p1x1 - p2x2 – i = 0.
И





сключив из этих уравнений неизвестную , получаем систему двух уравнений с двумя неизвестными x1 и x2 :
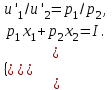 (41)
(41) Решение (x1*,x2*) системы уравнений (41) является решением задачи потребительского выбора.
В многомерном случае (39) также используется метод Лагранжа имеет вид:
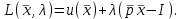
(42)
Далее, согласно условиям максимума , составляется система из (n+1) уравнений относительно (n+1) неизвестных
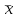 и
и 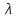 :
: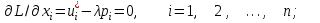 (43)
(43) 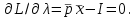
Исключая из этих уравнений неизвестную
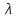 , получаем систему n уравнений относительно n неизвестных – координат точки условного максимума :
, получаем систему n уравнений относительно n неизвестных – координат точки условного максимума :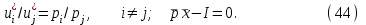
Решение
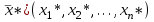 этой системы уравнений – точка условного экстремума - является решением общей задачи потребительского выбора.
этой системы уравнений – точка условного экстремума - является решением общей задачи потребительского выбора.Функции спроса
Решение задачи потребительского выбора
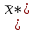 называется точкой спроса. Эта точка спроса зависит от цен
называется точкой спроса. Эта точка спроса зависит от цен 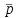 и дохода I. Иными словами, точка спроса является функцией цен и дохода, т.е. функцией спроса. В свою очередь, функция спроса представляет собой вектор-функцию п + 1 аргумента (в общем случае п цен р1, р2,…, рп, и дохода I), состоящую из п компонент:
и дохода I. Иными словами, точка спроса является функцией цен и дохода, т.е. функцией спроса. В свою очередь, функция спроса представляет собой вектор-функцию п + 1 аргумента (в общем случае п цен р1, р2,…, рп, и дохода I), состоящую из п компонент:х = х (р1, р2,…, рп, , I),
Таким образом, функция спроса – это набор п функций, каждая из которых зависит от п + 1 аргумента:
х1 = х1 (р1, р2,…, рп, , I),
х2 = х2 (р1, р2,…, рп, , I),
……………………………(45)
хп = хп (р1, р2,…, рп, , I.
Функции (45) называются функциямиспроса соответствующих товаров.
Пример 2.
Для набора из двух товаров на рынке, известных ценах на них р1 и р2 и доходе I найти функции спроса, если функция полезности имеет вид u ( x1 , x2 ) = x10,5 x20,5 .
Решение.
Дифференцируя данную функцию полезности, получаем
u1 = 0,5 x20,5 / x10,5, u2 = 0,5 x10,5 / x20,5.
Далее, подстановка в формулы (41) приводит к системе уравнений:
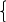 x2 / x1 = p1 / p2 ,
x2 / x1 = p1 / p2 ,p1
