ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 54
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
деп оларды бір нүктеден бастап салғанда пайда болатын бұрыштың шамасын айтамыз (62-сурет).
Қарама – қарсы бағытталған векторлардың арасындағы бұрыш 1800-қа, ал бағыттас векторлардың арасындағы бұрыш 00-қа тең.
Есеп.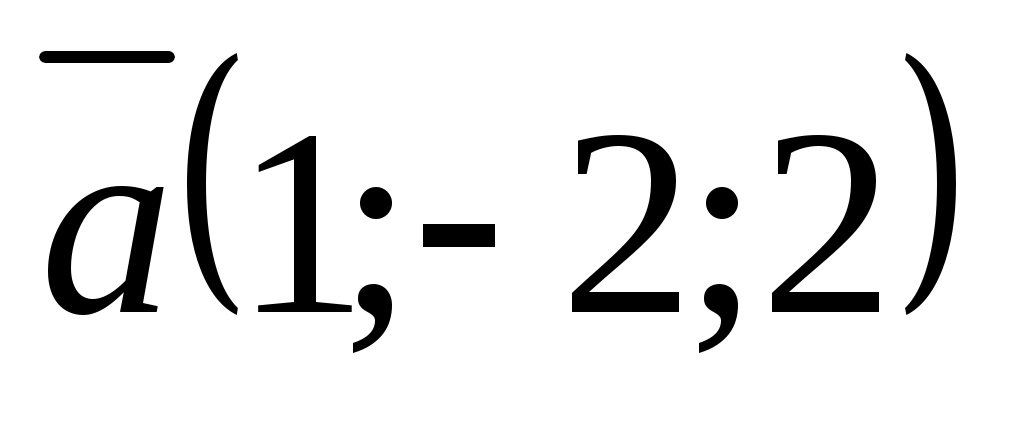 және
және 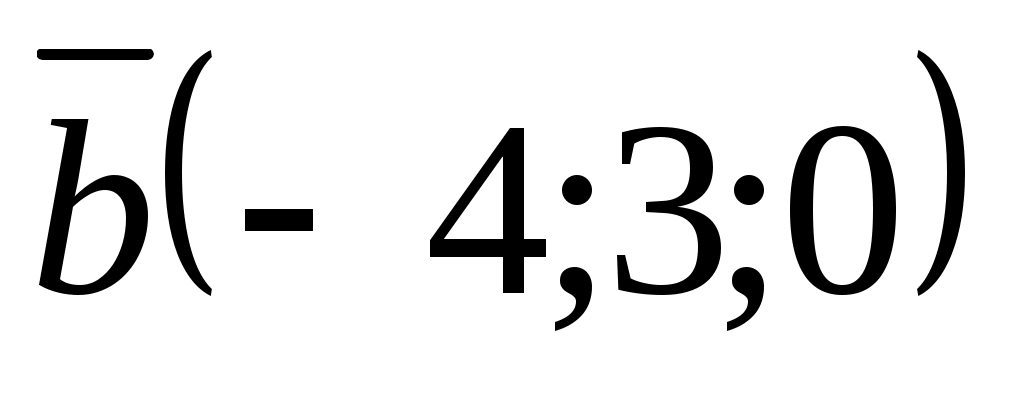 векторларының арасындағы бұрыштың косинусын табыңдар.
векторларының арасындағы бұрыштың косинусын табыңдар.
Шешуі.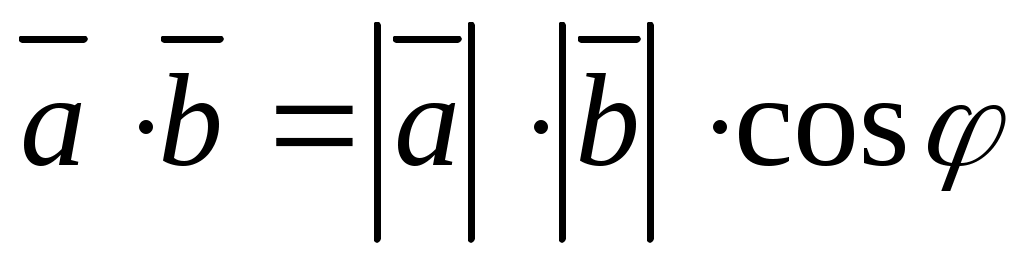 . Бұдан
. Бұдан
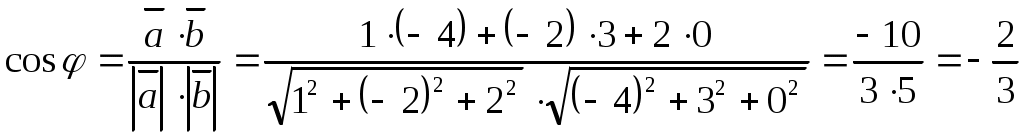 .
.
Жауабы: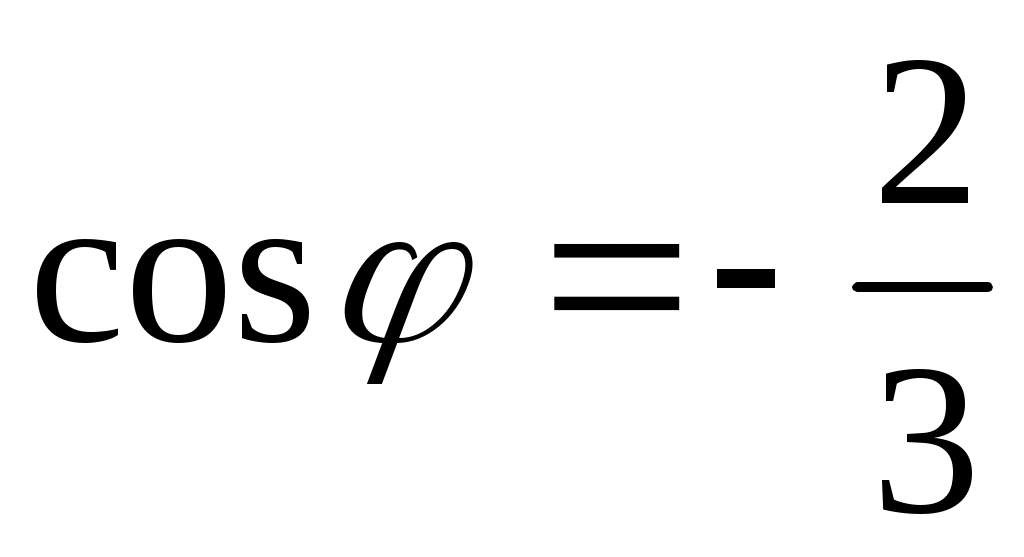 .
.
Тапсырмалар.
№19. Мына векторлардың скаляр көбейтіндісін табыңдар: 1)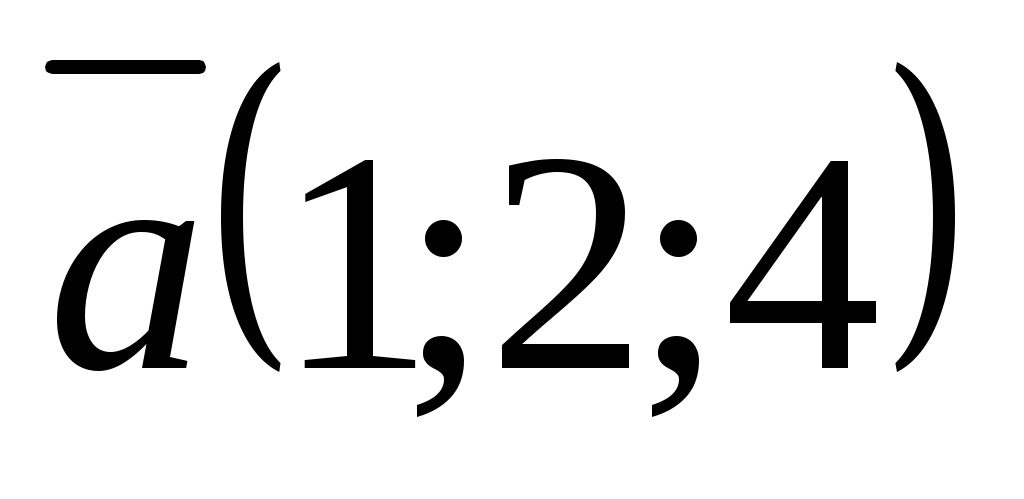 және
және 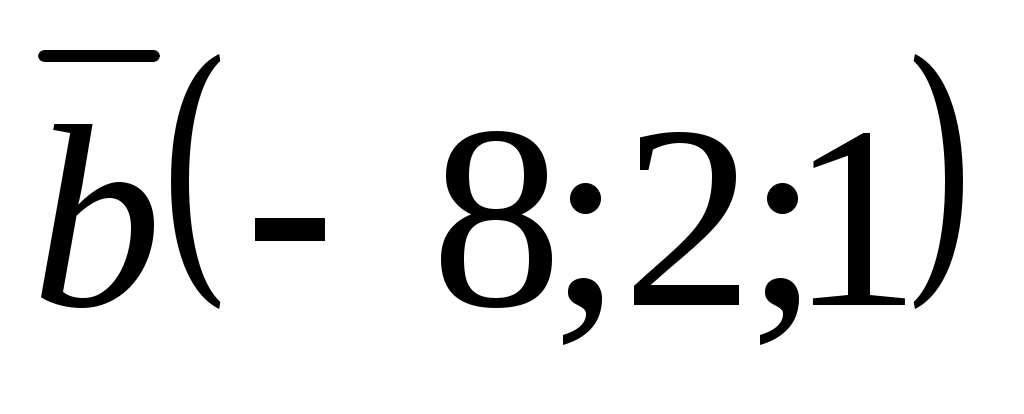 ; 2)
; 2) 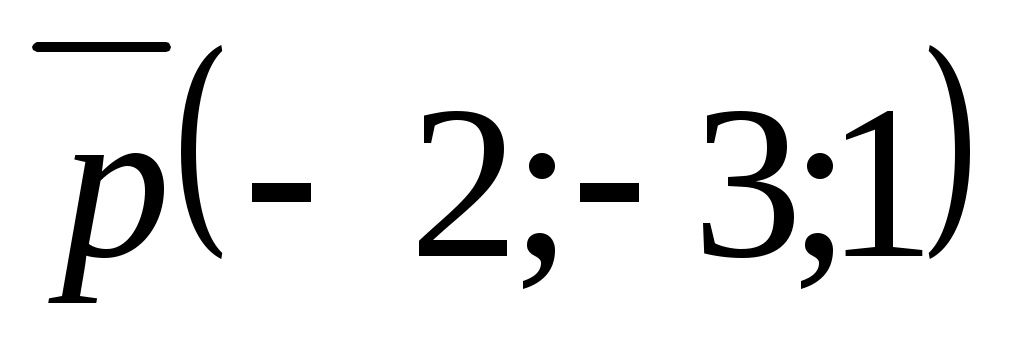 және
және 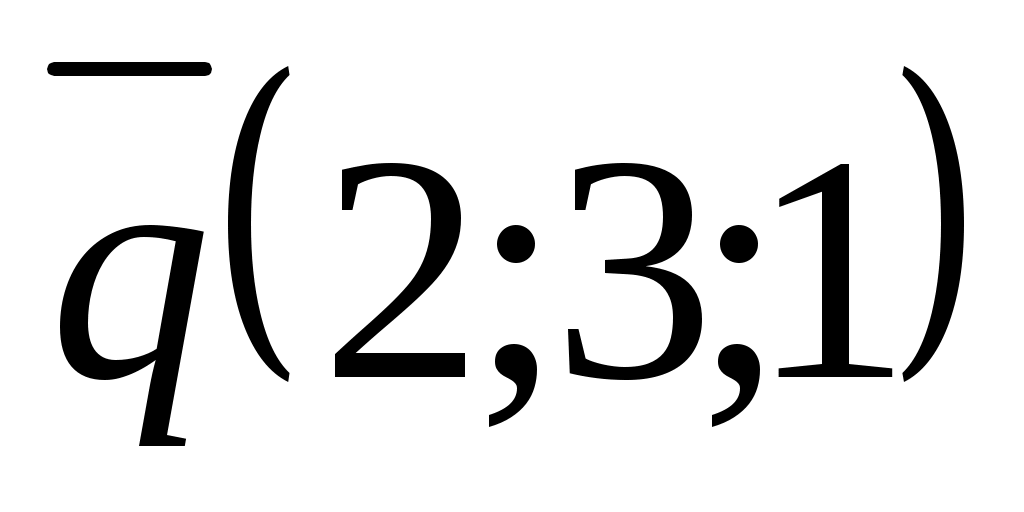 .
.
№20.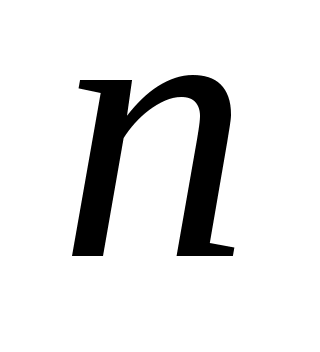 -нің қандай мәндерінде: 1)
-нің қандай мәндерінде: 1) 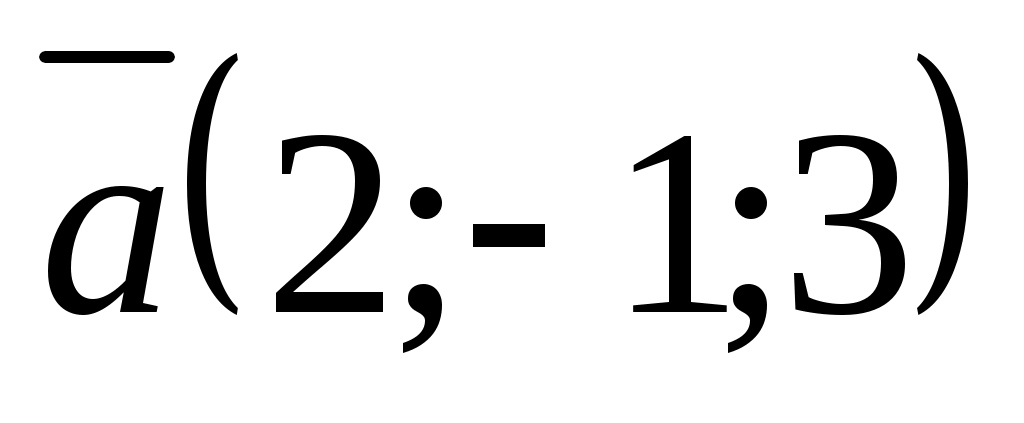 ,
, 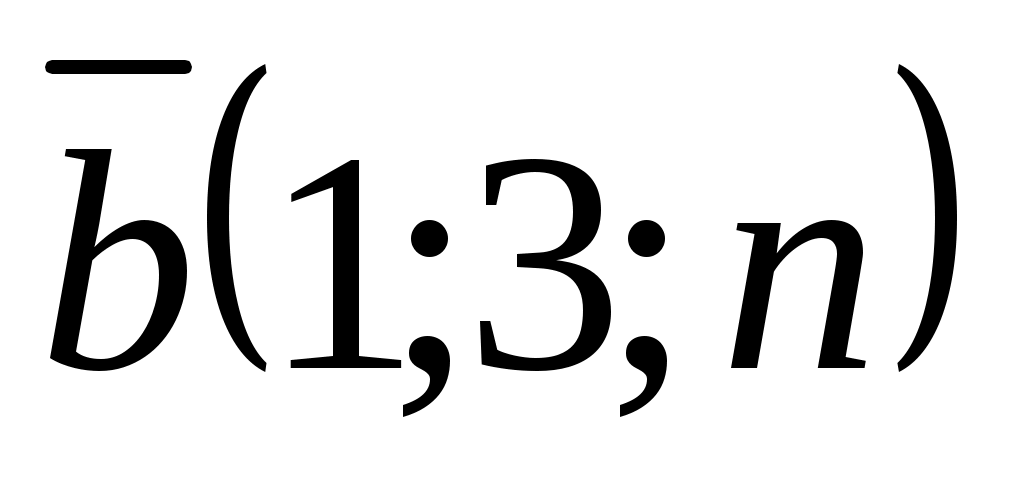 ; 2)
; 2) 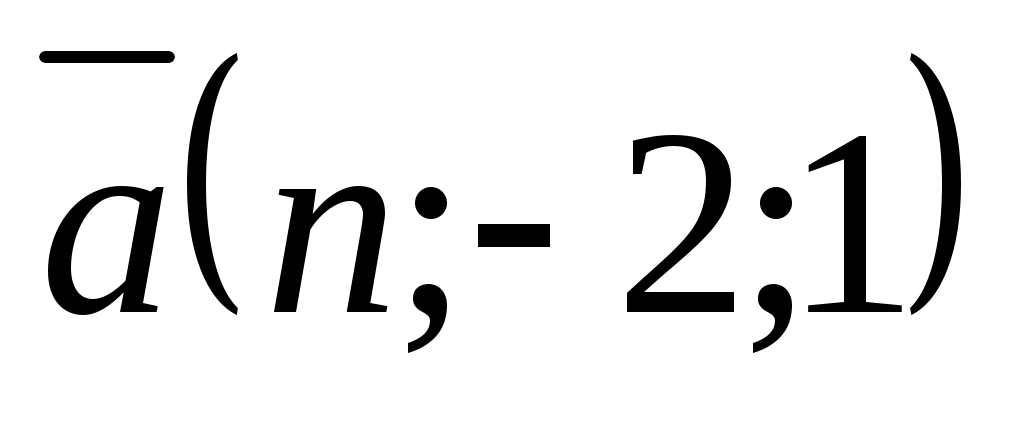 ,
, 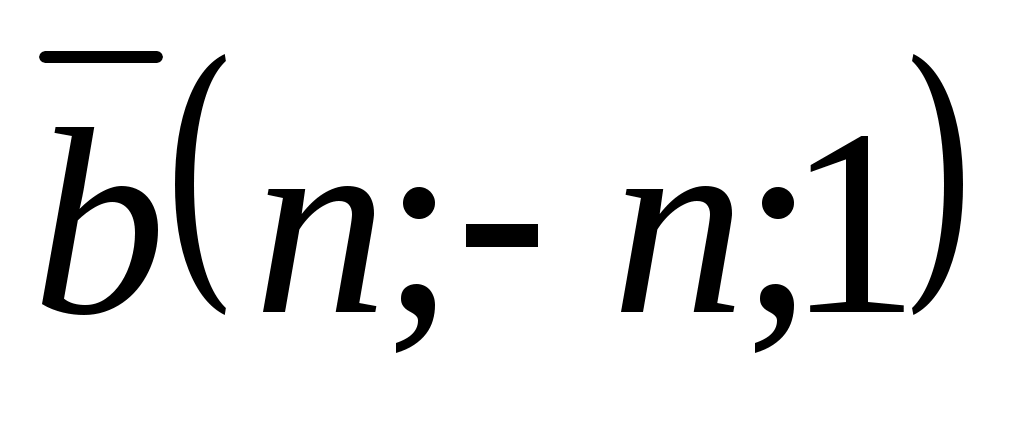 векторлары перпендикуляр болады?
векторлары перпендикуляр болады?
№21.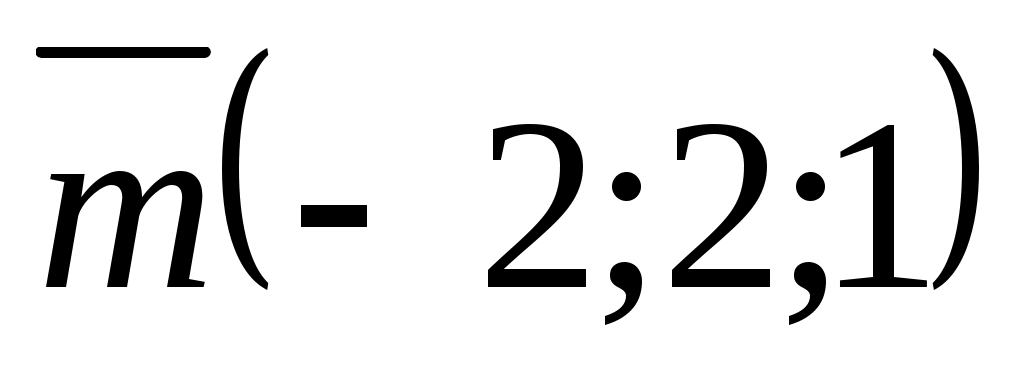 және
және 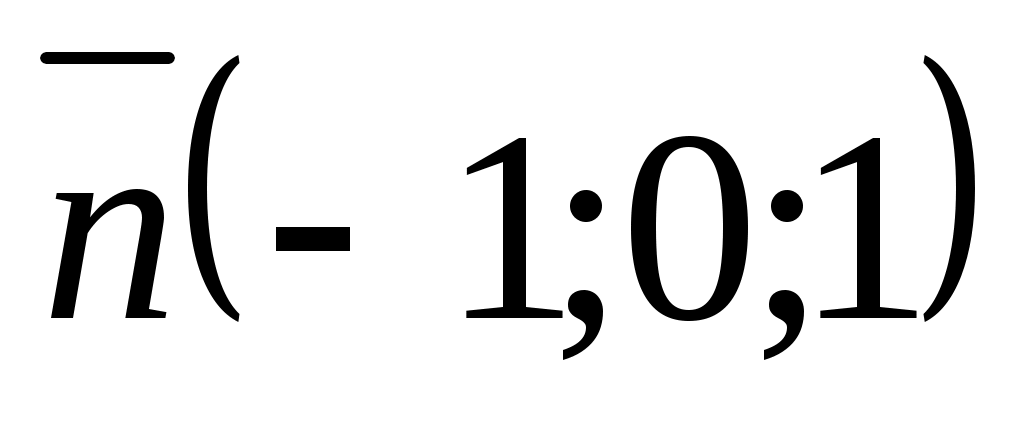 векторларының арасындағы бұрышты табыңдар.
векторларының арасындағы бұрышты табыңдар.
№22. Төрт нүкте берілген: А(0;1;-1), В(1;-1;2), С(3;1;0), D(2;-3;1).
және векторларының арасындағы бұрыштың косинусын табыңдар.
векторларының арасындағы бұрыштың косинусын табыңдар.
№23.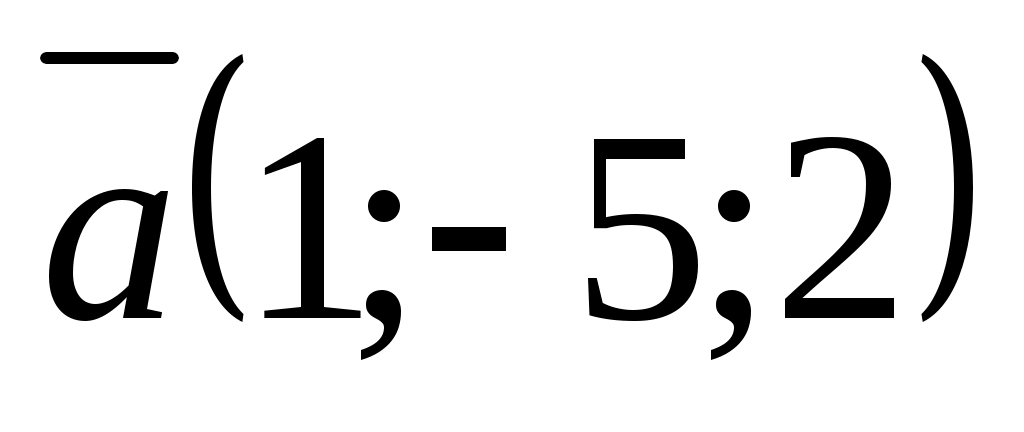 және
және 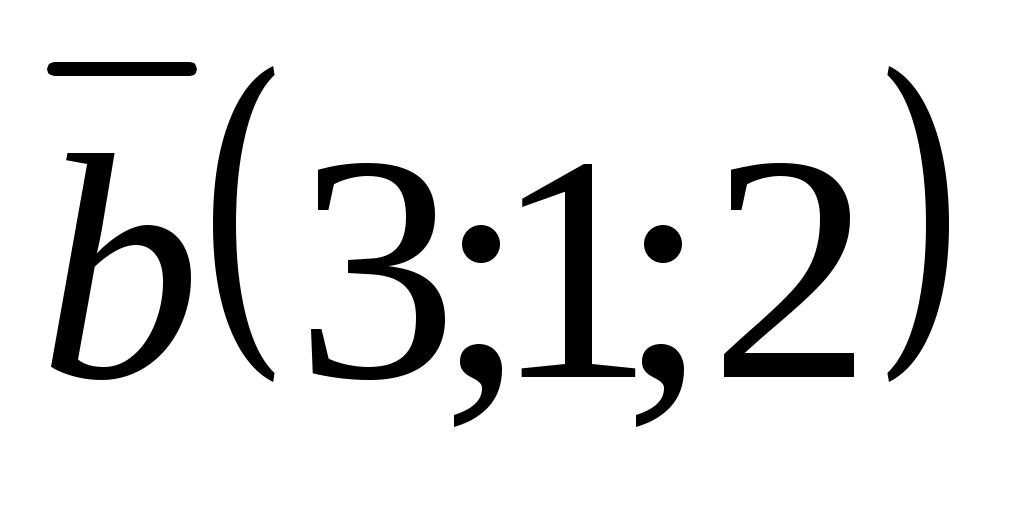 векторлары берілген.
векторлары берілген. 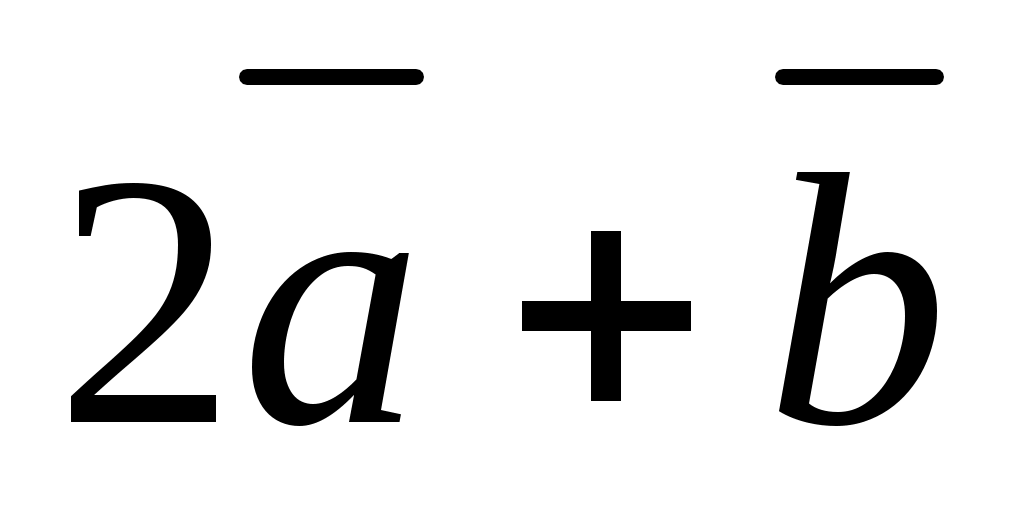 және
және 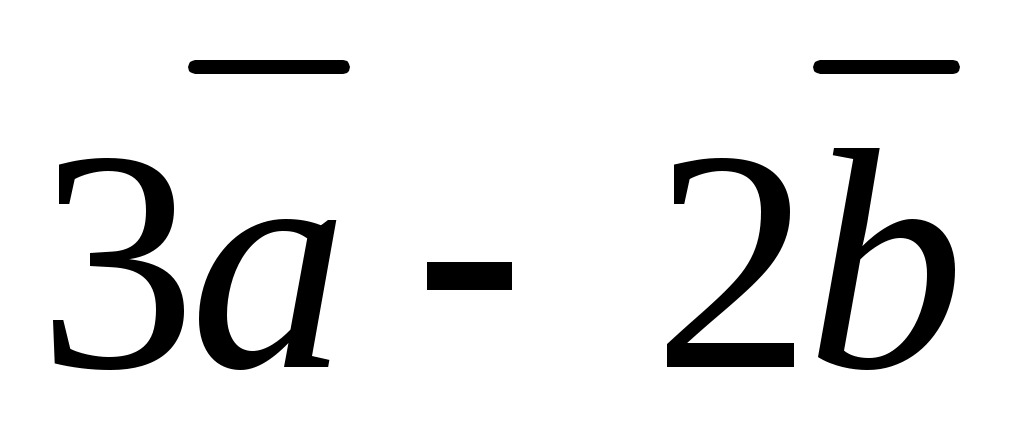 векторларының скаляр көбейтіндісі табыңдар.
векторларының скаляр көбейтіндісі табыңдар.
№24. А(0; 1; -1), В(1; -1; 2), С(3; 1; 0) нүктелері берілген. АВС үшбұрышындағы С бұрышының косинусын табыңдар.
§ 5. ПРИЗМА
5.1. Призманың анықтамасы.
Бұл параграфта біз көпжактың дербес түрлерінің бірі призмамен (11.1-сурет) танысамыз. Бұл фигура ерте ғасырлардан белгілі.
Призма пішіндес заттар үйлер салғанда кеңінен қолданылады (11.2-сурет). Призма сөзі гректің ргата — "кесілген бөлік" сөзінен алынған.
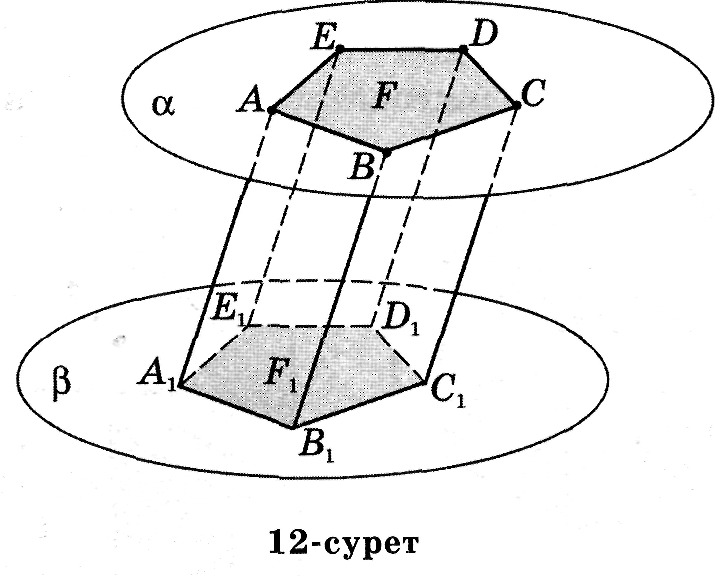
2-анықтама. Екі жагы параллель жазықтықтарда жататын өзара тец көпжақтар, ал цалган жақтары параллелограмдар болът келген көпжақты призма деп атайды (12-сурет).
11-сурет
Аталған параллелограмдар призманың бүйір жақтары деп аталады.
Параллель жазықтықтарда жататын Ғ және Ғ1көпбұрыштары призманың табандары, ал қалған жақтары бүйір жақтары деп аталады. Жоғарғы Ғ және төменгі Ғ1табандарының төбелерін қосатын кесінділер призманың бүйір қырлары деп аталады.
12-суреттегі АВСDЕ және А1В1С1D1Е1көпбұрыштары призманың табандары, ал АА1, ВВ1, СС1, DD1жөне ЕЕ1кесінділері — бүйір кырлары.
Призманың барлықбүйір қырларының параллелъ және тең(12-сурет).
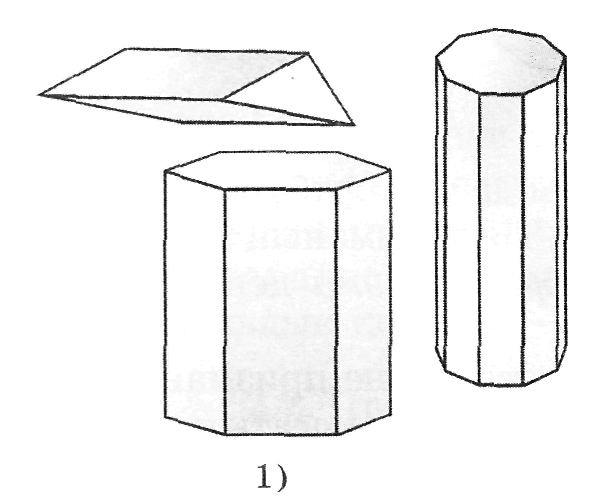
Табанының қабырғалар санына қарай призма үшбұрьппты, төрт-бұрышты, ..., п бұрышты болып бөлінеді (13-сурет).
13-сурет
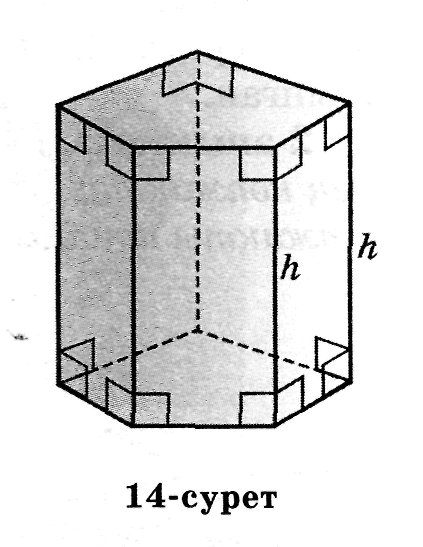
Егер призманың барлық бүйір жақтары да тіктөртбұрыш болып келсе, ол тік призма деп аталады (14-сурет). Тік призманың табанында дұрыс көпбұрыш жатса, онда призма дұрыс призма деп аталады (15-сурет).
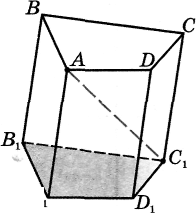
Призманыц диагоналі — оның ішімен өтетін жөне призманың екі табанының (бір бүйір жағында жатпайтын) төбелерін қосатын кесінді. 16-суреттегі АС1кесіндісі — призманың диагоналі.
Табандарының арасында оларға перпендикуляр орналасқан кесінді призманыц биіктігі деп аталады (осы кесіндінің ұзындығын да биіктігі деп атай береміз). 17-суреттегі СН кесіндісі призманың биіктігі.
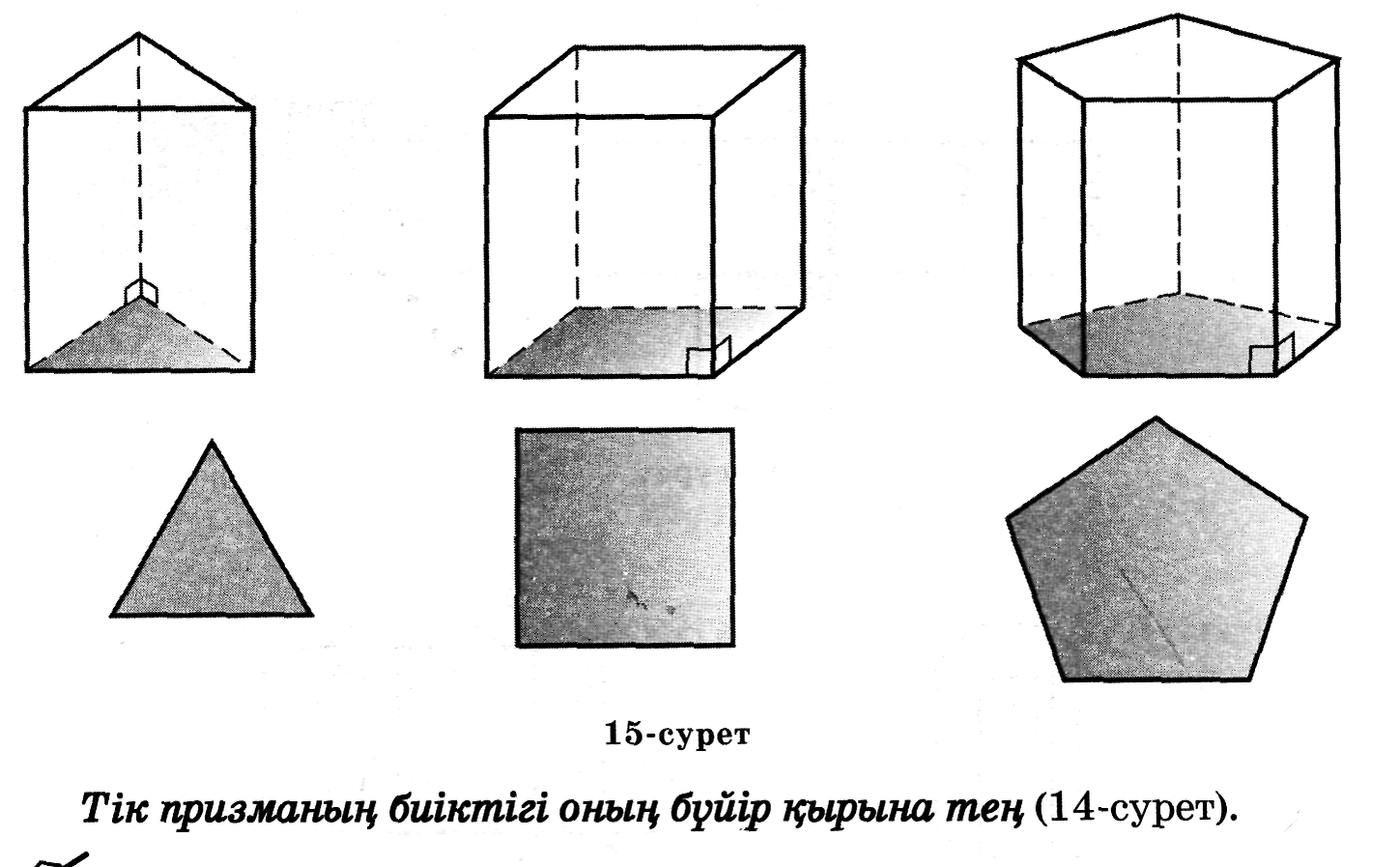
Тік призманың биіктігі оның бүйір қырына тең (14-сурет).
Призманың бір жағында жатпайтын екі бүйір қыры аркылы өтетінжазыктықпен кимасы оның диагоналъдыц цимасы деп аталады.
Мысалы, АСС1А1 және ЕСС1Е1 – призманың диагональдық қималары (18-сурет).
Кез келген призманың диагональдық қимасы – параллелограмм, ал тік призманың диагональдық қимасы – тіктөртбұрыш.
5.2. Призма бетінің ауданы
Бізге көпжақтың беті саны шектеулі көпбұрыштардан (жақтардан) тұратыны белгілі.
Призманың бүйір жақтарының бірігуі оның бүйір беті деп аталады. Призманың табандары мен бүйір бетінің бірігуі призманың толық беті деп аталады.
Анықтама. Призманың бүйір бетінің ауданы деп оның бүйір жақтарының аудандарының қосындысын айтады; толық бетінің ауданы деп оның барлық жақтарының аудандарының қосындысын айтады. Призманың бүйір бетінің ауданын Sпр.б.б (23-сурет) деп, толық бетін Sпр.т.б (24-сурет) деп белгілейміз.

1 -теорема. Тік призманың бүйір бетінің ауданы оның табанының периметрін призманың биіктпігіне көбейтпкенге тең, яғни
Sп 6 б= Р • һ,мұндағы Р — призма табанының периметрі, һ—тік призманың биіктігі.
2-теорема.Призманьщтолыцбетініцауданы оньщ буйір бетінің ауданы мен екі еселенген табан ауданының қосындысына тең:
Sпр.т.б=Sпр.б.б+2Sтаб.
Тапсырмалар.
№25. Дұрыс төртбұрышты призманың бір бүйір жағының ауданы 6дм2. Оның бүйір бетінін ауданын табыңдар.
№26. Табанының қабырғасы 5см, ал бүйір жағының диагоналі 13см-ге тең дұрыс төртбұрышты призманың биіктігін табыңдар.
№27. Үшбұрышты тік призманың бүйір кыры 4см, ал табанының қабырғалары 3см, 5см жөне 6см. Призманың бүйір бетінің ауданын табьщдар.
№28. Үшбұрышты көлбеу призманың бүйір кыры 8см, ал бүйір қырларының арақашыктықтары 3см, 4см, 5см. Призманың бүйір бетінің ауданын табыңдар.
№29. Үшбұрышты тік призманың барлык кырлары тең. Оның бүйір бетінің ауданы 48 см2. Призманың толык бетінің ауданын табыңдар.
№30. Дұрыс алтыбұрышты призманың бүйір бетінің ауданы 72 дм2, ал бүйір жағының диагоналі 5см. Призманың биіктігін жөне табанының кабырға-
сын табыңдар.
№31. Дұрыс төртбұрышты призманың толық бетінің ауданы 80 дм2, бүйір бетінің ауданы 64 дм2. Призманың биіктігін табыңдар.
№32. Үшбұрышты көлбеу призманың екі бүйір жағы өзара перпендикуляр. Олардың ортақ қыры 4,8м жөне қалған екі бүйір кырынан 1,2м, 3,5м кашықтықта орналасқан. Призманың бүйір бетінің ауданын табыңдар.
№33. Көлбеу призманын бүйір қыры оның табан жазықтығымен 30° бұрыш жасайды. Призманың бүйір кыры 12см. Оның биіктігін табыңдар.
№34. Кубтың карама-карсы екі қыры арқылы жүргізілген қимасының ауданы 64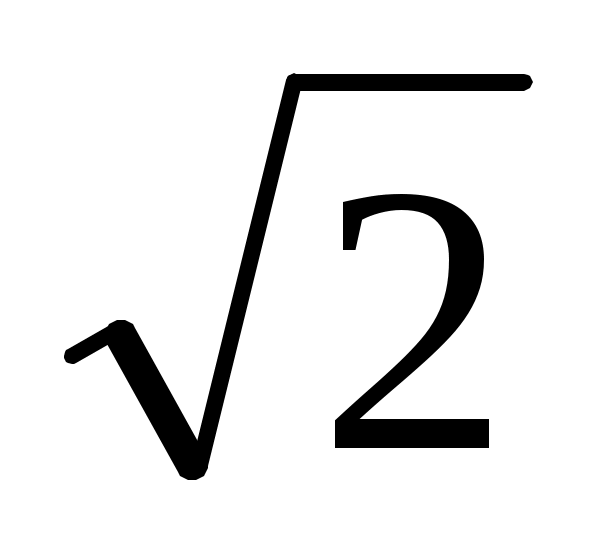 см2-ге тең. Кубтың қырын және диагоналін табыңдар.
см2-ге тең. Кубтың қырын және диагоналін табыңдар.
№35. Тік призманың табаны — тікбұрышты үшбұрыш. Гипотенузаның ортасы арқылы оған перпендикуляр қима жүргізілген. Егер табанының катеттері
20см жөне 21см, ал призманың бүйір кыры 42см болса, қиманың ауданы
неге тең?
Қарама – қарсы бағытталған векторлардың арасындағы бұрыш 1800-қа, ал бағыттас векторлардың арасындағы бұрыш 00-қа тең.
| Теорема. Векторлардың скаляр көбейтіндісі олардың модульдерін сол векторлар арасындағы бұрыштың косинусына көбейткенде шығатын санға тең болады, яғни |  |
Есеп.
Шешуі.
Жауабы:
Тапсырмалар.
№19. Мына векторлардың скаляр көбейтіндісін табыңдар: 1)
№20.
№21.
№22. Төрт нүкте берілген: А(0;1;-1), В(1;-1;2), С(3;1;0), D(2;-3;1).
және
№23.
№24. А(0; 1; -1), В(1; -1; 2), С(3; 1; 0) нүктелері берілген. АВС үшбұрышындағы С бұрышының косинусын табыңдар.
§ 5. ПРИЗМА
5.1. Призманың анықтамасы.
Бұл параграфта біз көпжактың дербес түрлерінің бірі призмамен (11.1-сурет) танысамыз. Бұл фигура ерте ғасырлардан белгілі.
Призма пішіндес заттар үйлер салғанда кеңінен қолданылады (11.2-сурет). Призма сөзі гректің ргата — "кесілген бөлік" сөзінен алынған.
2-анықтама. Екі жагы параллель жазықтықтарда жататын өзара тец көпжақтар, ал цалган жақтары параллелограмдар болът келген көпжақты призма деп атайды (12-сурет).
 |  |
11-сурет

Аталған параллелограмдар призманың бүйір жақтары деп аталады.
Параллель жазықтықтарда жататын Ғ және Ғ1көпбұрыштары призманың табандары, ал қалған жақтары бүйір жақтары деп аталады. Жоғарғы Ғ және төменгі Ғ1табандарының төбелерін қосатын кесінділер призманың бүйір қырлары деп аталады.
12-суреттегі АВСDЕ және А1В1С1D1Е1көпбұрыштары призманың табандары, ал АА1, ВВ1, СС1, DD1жөне ЕЕ1кесінділері — бүйір кырлары.
Призманың барлықбүйір қырларының параллелъ және тең(12-сурет).
Табанының қабырғалар санына қарай призма үшбұрьппты, төрт-бұрышты, ..., п бұрышты болып бөлінеді (13-сурет).
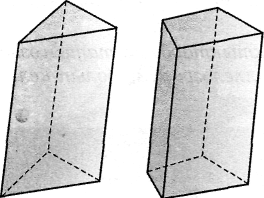 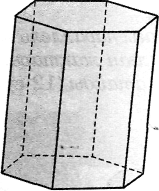 |  |
13-сурет
Егер призманың барлық бүйір жақтары да тіктөртбұрыш болып келсе, ол тік призма деп аталады (14-сурет). Тік призманың табанында дұрыс көпбұрыш жатса, онда призма дұрыс призма деп аталады (15-сурет).
Призманыц диагоналі — оның ішімен өтетін жөне призманың екі табанының (бір бүйір жағында жатпайтын) төбелерін қосатын кесінді. 16-суреттегі АС1кесіндісі — призманың диагоналі.
Табандарының арасында оларға перпендикуляр орналасқан кесінді призманыц биіктігі деп аталады (осы кесіндінің ұзындығын да биіктігі деп атай береміз). 17-суреттегі СН кесіндісі призманың биіктігі.

Тік призманың биіктігі оның бүйір қырына тең (14-сурет).
Призманың бір жағында жатпайтын екі бүйір қыры аркылы өтетінжазыктықпен кимасы оның диагоналъдыц цимасы деп аталады.
 16-сурет | 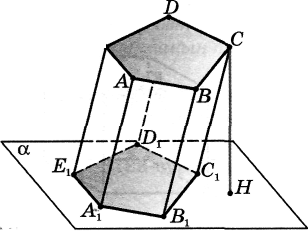 17-сурет |
Мысалы, АСС1А1 және ЕСС1Е1 – призманың диагональдық қималары (18-сурет).
Кез келген призманың диагональдық қимасы – параллелограмм, ал тік призманың диагональдық қимасы – тіктөртбұрыш.
5.2. Призма бетінің ауданы
Бізге көпжақтың беті саны шектеулі көпбұрыштардан (жақтардан) тұратыны белгілі.
Призманың бүйір жақтарының бірігуі оның бүйір беті деп аталады. Призманың табандары мен бүйір бетінің бірігуі призманың толық беті деп аталады.
Анықтама. Призманың бүйір бетінің ауданы деп оның бүйір жақтарының аудандарының қосындысын айтады; толық бетінің ауданы деп оның барлық жақтарының аудандарының қосындысын айтады. Призманың бүйір бетінің ауданын Sпр.б.б (23-сурет) деп, толық бетін Sпр.т.б (24-сурет) деп белгілейміз.

1 -теорема. Тік призманың бүйір бетінің ауданы оның табанының периметрін призманың биіктпігіне көбейтпкенге тең, яғни
Sп 6 б= Р • һ,мұндағы Р — призма табанының периметрі, һ—тік призманың биіктігі.
2-теорема.Призманьщтолыцбетініцауданы оньщ буйір бетінің ауданы мен екі еселенген табан ауданының қосындысына тең:
Sпр.т.б=Sпр.б.б+2Sтаб.
Тапсырмалар.
№25. Дұрыс төртбұрышты призманың бір бүйір жағының ауданы 6дм2. Оның бүйір бетінін ауданын табыңдар.
№26. Табанының қабырғасы 5см, ал бүйір жағының диагоналі 13см-ге тең дұрыс төртбұрышты призманың биіктігін табыңдар.
№27. Үшбұрышты тік призманың бүйір кыры 4см, ал табанының қабырғалары 3см, 5см жөне 6см. Призманың бүйір бетінің ауданын табьщдар.
№28. Үшбұрышты көлбеу призманың бүйір кыры 8см, ал бүйір қырларының арақашыктықтары 3см, 4см, 5см. Призманың бүйір бетінің ауданын табыңдар.
№29. Үшбұрышты тік призманың барлык кырлары тең. Оның бүйір бетінің ауданы 48 см2. Призманың толык бетінің ауданын табыңдар.
№30. Дұрыс алтыбұрышты призманың бүйір бетінің ауданы 72 дм2, ал бүйір жағының диагоналі 5см. Призманың биіктігін жөне табанының кабырға-
сын табыңдар.
№31. Дұрыс төртбұрышты призманың толық бетінің ауданы 80 дм2, бүйір бетінің ауданы 64 дм2. Призманың биіктігін табыңдар.
№32. Үшбұрышты көлбеу призманың екі бүйір жағы өзара перпендикуляр. Олардың ортақ қыры 4,8м жөне қалған екі бүйір кырынан 1,2м, 3,5м кашықтықта орналасқан. Призманың бүйір бетінің ауданын табыңдар.
№33. Көлбеу призманын бүйір қыры оның табан жазықтығымен 30° бұрыш жасайды. Призманың бүйір кыры 12см. Оның биіктігін табыңдар.
№34. Кубтың карама-карсы екі қыры арқылы жүргізілген қимасының ауданы 64
№35. Тік призманың табаны — тікбұрышты үшбұрыш. Гипотенузаның ортасы арқылы оған перпендикуляр қима жүргізілген. Егер табанының катеттері
20см жөне 21см, ал призманың бүйір кыры 42см болса, қиманың ауданы
неге тең?
