ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 57
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Параллель қиманың ауданының пирамида табанының ауданына қатынасы пирамида төбесінен қимаға дейінгі қашықтықтың квадратының пирамида биіктігінің квадратына қатынасына тең болады.
. (52-сурет)Дұрыс пирамидадан алынған қиық пирамиданы дұрыс қиық пирамида дейді. Бүйір жағының биіктігі дұрыс қиық пирамиданың апофемасы деп аталады. 52.2-суреттегі М1М кесіндісі дұрыс қиық пирамиданың апофемасы.
Дұрыс қиық пирамиданың
• бүйір жақтары тең;
• бүйір қырлары тең;
• апофемалары тең;
• әрбір табан қабырғасындағы екіжақты бұрыштары тең;
• бүйір қырларындағы екіжақты бұрыштары теңболатынын дәлелдеуге болады.
Теорема. Дұрыс қиықпирамиданыңбүйірбеті оның табандарыныңпериметрлерініңқосындысының жартысын апофемасына көбейткенге тең, яғни
Sқ.пир.б.б=
(P+P1)kмұндағы Р және Рг— пирамида табандарының периметрлері.
Тапсырмалар.
№64. Табандарының қабырғалары 7см және 5см, ал апофемасы 2см болатын дұрыс төртбұрышты қиық пирамиданың бүйір бетінің және толық бетінің аудандарын табыңдар.
№65. Табандарының кабырғалары 10см және 4см, ал бүйір қыры 5см болатын дұрыс үшбұрышты қиық пирамиданың бүйір бетінің және толық бетінің аудандарын табыңдар.
№66. Дұрыс төртбұрышты қиық пирамиданың жоғарғы табанының қабырғасы 1 см-ге тең, ал төменгі табан қабырғасы одан бес есе ұзын. Пирамиданың бүйір бетінің ауданы 24
см2-ге тең. Қиық пирамиданың апофемасын және биіктігін табыңдар.§9. Цилиндр
9.1. Цилиндр – айналу денесі
Геометриялык фигура — цилиндрді өмірде жиі кездестіреміз (63-сурет). Бұл фигураны қалай анықтап, қалай салуға болады?
Тіктөртбұрышты оның бір қабырғасын қамтитын осьтен айналдыру арқылы цилиндрді алуға болады. 64.1 -суретте Ғ тіктөртбұрышы және оның бір қабырғасын қамтитын l осі берілген.
Егер осы F тіктөртбұрышын l осінен айналдырсақ, онда біз айналу денесі (фигурасы) – цилиндрді аламыз (64,2-сурет).
Анықтама. Цилиндр деп тіктөртбұрышты оның қабырғаларының бірінен айналдырғанда шығатын фигураны (денені) атайды.
| 65-суретте АОО1В тіктөртбұрышын оның ОО1кабырғасын қамтитын l осінен айналдырғанда шыққан цилиндр бейнеленген. АОО1В тіктөртбұрышының ОО1осіне параллель АВ қабырғасы цилиндрдің бүйір беті деп аталатын қисық бетті жасайды және ол цилиндрдің жасаушысы деп аталады. АО жөне О1В кесінділерінің айналуынан цилиндрдің табандары депаталатын өзара тең екі дөңгелек аламыз. Сонымен цилиндрдің беті цилиндрдің табандары. деп аталатын екі дөңгелектен және цилиндрдің бүйір бетінен тұрады. |  |
Жасаушының ұзындығы цилиндрге биіктік болып табылады. Ол табан жазықтықтарының арақашықтығына, яғни ОО1 кесіндісінің ұзындығына тең.
| Цилиндрдің жазықтықпен қимасы деп жалғыз нүктеден, цилиндрдің жасаушы-сынан немесе табанынан өзгеше фигураны, яғни аталғандардан өзге цилиндр мен жазықтықтың ортақ бөлігін атайды. Қиманы цилиндрдің осі арқылы жүргізуге болады (67-сурет). Мұндай қималар остікқималар деп аталады. Осьтік қиманың қабырғалары табандарының диаметрлерінен және екі жасаушыдан тұрады. |  |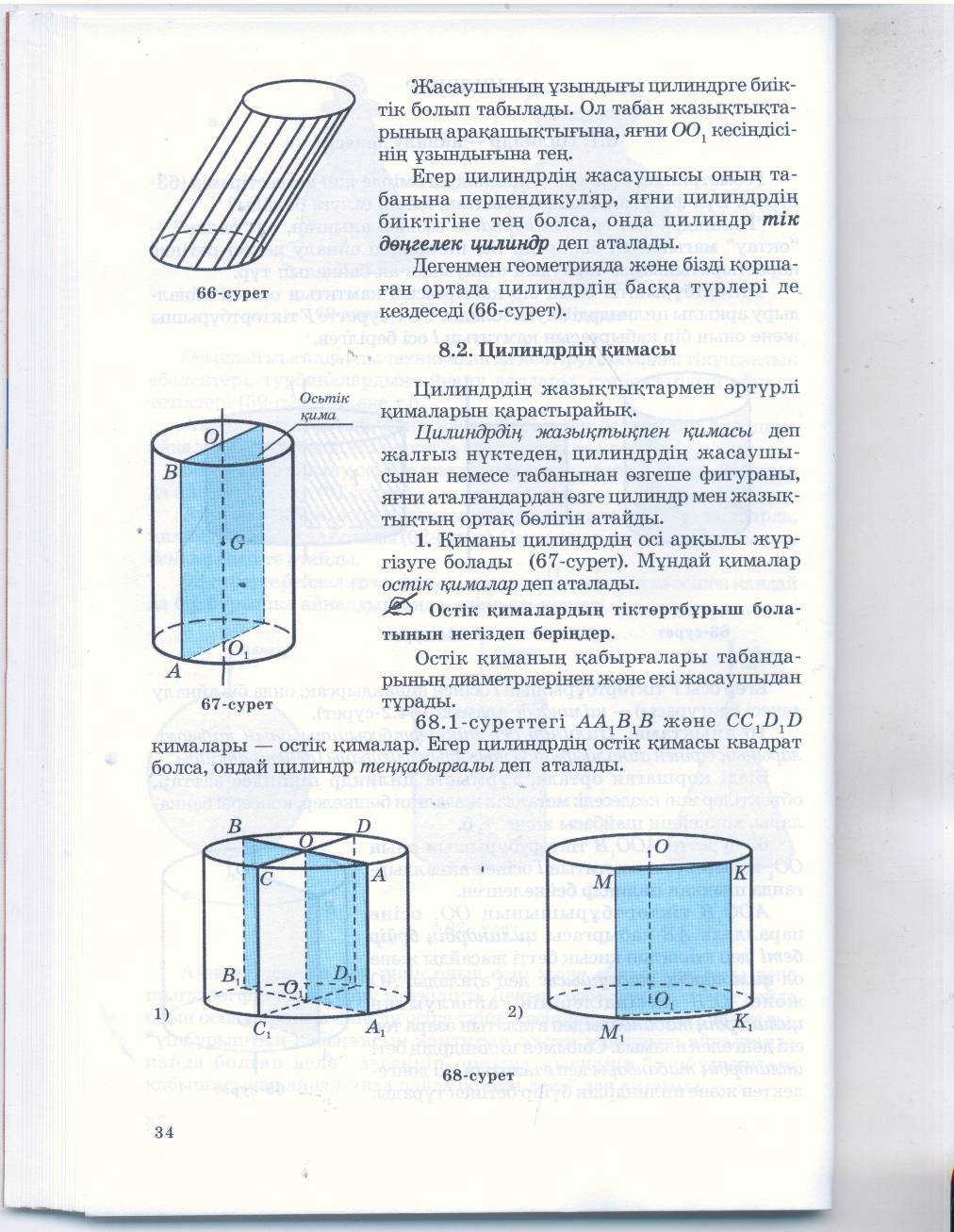
9.2. Цилиндр бетінің ауданы.
Егер цилиндрдің бетін табан шеңберлері бойымен және қайсыбір жасаушысының бойымен киып алып жазып жіберсек, цилиндрдің жазбасын аламыз (72-сурет). Цилиндр бетінің жазбасы тіктөртбұрыштан және өзара тең екі дөңгелектен тұрады.
Егер цилиндрдің радиусы R, ал биіктігі Н болса, онда оның бүйір беті қабырғаларының ұзындығы 2
R мен Н болатын тіктөртбұрышқа жазылады. Осы жазбаның ауданы 2 RН
цилиндрдің бүйір бетінің аудаyы ретінде алынады.
Сонымен, біз мына теореманы дәлелдедік.
Теорема. Цилиндрдіц бүйір бетініңаудан. табан шеңберініңұзындығын оның биіктігіне көбейткенге тең, яғни
Sц.б.б=2
RH.Цилиндрдің толық бетінің ауданын Sцтб табу үшін оның бүйір бетінің ауданына табандарының аудандарын қосу керек:
Sц.т.б=2
RH+2 R2 немесе
Sц.т.б=2
R(H+R)№67. Цилиндрдің радиусы 3см, биіктігі 8см. Цилиндрдің осьтік қимасы диагоналінің ұзындығын табыңдар.
№68. Цилиндрдің осьтік қимасы — квадрат. Оның ауданы 196см2-ге тең. Цилиндрдің табанының ауданын табыңдар.
№69.Цилиндрдің радиусы 6см, осьтік қимасының диагоналі 13см. а) Цилиндрдің биіктігін; ә) осьтік қимасының ауданын; б) бүйір бетінің ауданын; в) цилиндрдің толық бетінің ауданын табыңдар.
№70. Тіктөртбұрыштың қабырғалары 4см және 5см. Тіктөртбұрыштың кіші
қабырғасынан айналганда шыққан дененің толық бетінің ауданын табыңдар.
№71. Цилиндрдің ауданы және бүйір бетінің ауданы сәйкесінше 50см2 және 30см2-ге тең. Цилиндрдің радиусы мен биіктігін табыңдар.
№72. Радиусы 2см жөне биіктігі 4см-ге тең цилиндр берілген. Оның осінен 1см, қашықтықта оське параллель қима жүргізілген. Қиманың ауданын және периметрін табыңдар (73-сурет).
№73. Цилиндрдін биіктігі 16см, радиусы 10см. Цилиндрдің осіне параллель және одан 6см қашықтықта өтетін қиманың ауданын табындар.
№74. Цилиндрдің табан радиусы мен биіктігі 5см-ге тең. Цилиндрге оның осіне және өзара параллель екі қима жүргізілген. Бұл қималардың аудандары 40см2 жөне 30см2. Қималардың арақашықтығын табыңдар.
№75. Цилиндрдің радиусы 5дм, ал биіктігі 8дм. Цилиндрдің табанына перпендикуляр және табан шеңберінен 60° доға қиьш түсіретін қиманың ауданын табыңдар.
§10. КОНУС
10.1. Конус — айналу денесі
Тағы да бір ерекше геометриялық фигураны — конусты қарастырайық (74.1-сурет).
Бізге Q тікбұрышты үшбұрышы берілсін (74.2-сурет). Егер осы тікбұрышты үшбұрышты оның катеті аркылы өтетін l осінен айналдырсақ, нәтижесінде, айналу денесі — конусты аламыз (74. 3-сурет).
Анықтама. Тікбұрышты үшбұрышты катетінен айналдырғанда шығатын фигура конус деп аталады.
74.3-суретте О бұрышы тік болатын ҒАО үшбұрышын оның ҒО катетінен айналдырғанда алынған конус бейнеленген. Осы суретті және жинақталған ақпараттарды пайдаланып, конустың мынадай қасиеттерін алуға болады:
1. ОА катеті айналғанда конустың табаны деп аталатын дөңгелекті сызып шығады.
2. Конустың табан жазықтығы оның ҒО осіне перпендикуляр,
ҒОА=90°. Енді біз конустың биіктігін анықтай аламыз.Анықтама. Конустың төбесінен оның табан жазықтығына жүргізілген перпендикуляр конустың биіктігі деп аталады.
3. ҒА гипотенузасы осьтен айналғанда конустың бүйір бетін сызып шығады. Табан шеңберінің кез келген нүктесін конустың Ғ төбесімен қосатын кесінділердің проекциялары тең, сондықтан олар өзара тең кесінділер. Бұл кесінділер конустың жасаушылары деп аталады.
10.2. Конустың бетінің ауданы
Егер конустың бүйір бетін қайсыбір жасаушысының бойымен, мысалы, АВ-ның бойымен қиып жазықтыққа жазсақ, онда конустың бүйір бетінің жазбасын аламыз (78.1-сурет).
Конус табанының радиусы R, жасаушысының ұзындығы l, ал биіктігі H болсын (78.2-сурет), яғни осінен айналғанда қарастырылып отырған конус шығатын тікбұрышты үшбұрыштың қабырғалары белгілі дейік. Пифагор теоремасына сөйкес бұл шамалар
l2 =R2+H2
теңдігімен байланысады.
Демек, бұл шамалардың екеуін білсек, үшіншісін таба аламыз. Конус табанының ауданы
R2-ка тең екені белгілі. Ал конустың бүйір бетінің ауданын
өлшеу үшін оның бүйір бетін жасаушыларының бірінің бойымен "қиып", жазықтыққа жазамыз. Сонда радиусы l-ге тең дөңгелектің секторын аламыз (78.2-сурет).
Конустыңбүйірбетініңауданыдегеніміз — осы сектордың ауданы. Оны есептеу үшін алынған секторға сәйкес бұрыштың
градустық шамасын табамыз. Оның доғасының ұзындығы конустың табан шеңберінің ұзындығына, яғни 2 R-ге тең. Екінші жағынан градустық өлшемі -ге тең сектор доғасының ұзындығы 
болады. Сондықтан,2
R= , бұдан 
.Sсек
өрнегіне -дің табылған мәнін қойсақ, конустың бүйір бетінің ауданын есептеу формуласын аламыз:Sкон.б.б
Сонымен, біз мынадай қорытындыға келдік.
Теорема. Конустыц бүйір бетінің ауданы оның табан шеңберінің ұзындығы мен жасаушысының көбейтіндісінің жартысына тең, ягни
Sкон.б.б
мұндағы R — конус табанынын радиусы, l — конустың жасаушысы.
Конус бетінің ауданы немесе конустың толык бетінің ауданы үшін оның жазбасының SТОЛЫК ауданы алынады. Ол конустың бүйір бетінің ауданы мен табанының ауданының қосындысынан тұрады (78-сурет).
Sкон.т.б =
Rl + R2 = R(l+R), мұндағы l — конустың жасаушысы, R— табанының радиусы.Тапсырмалар.
№76. Конустың биіктігі 15см, радиусы 8см. Конустың жасаушысын табыңдар.