ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.10.2024
Просмотров: 53
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
§6. Параллелепипедтер.
6.1. Параллелепипедтің анықтамасы.
Анықтама. Табандары параллелограмдар болатын призманы параллелепипед деп атайды (27-сурет).
Қарама-қарсы жақтарының үш жұбының қай-қайсысын да табандары ретінде ала беруге болады.
Паралелепипедке төрт диагональ жүргізуге болады. 28-суретте ABCDA1B1C1D1 параллелепипедінің диагональдары – AC1, BD1, CA1, DB1.
Анықтама. Барлық жақтары тіктөртбұрыш болатын параллелепипедті тікбұрышты параллелепипед деп атайды (29-сурет).
Тікбұрышты параллелепипедтің бір төбесінен шығатын үш қырының ұзындығы оның өлшемдері деп аталады. 30.1-суретте өлшемдері a, b, c болатын тікбұрышты параллелепипед бейнеленген.
Барлық өлшемдері тең тікбұрышты параллелепипед куб деп аталады (30.2-сурет). Кубтың барлық жақтары квадраттар.
Теорема. Тікбұрышты параллелепипедтің диагоналінің квадраты, оның бір төбесінен шығатын қабырғаларының квадраттарының қосындысына тең (32-сурет).
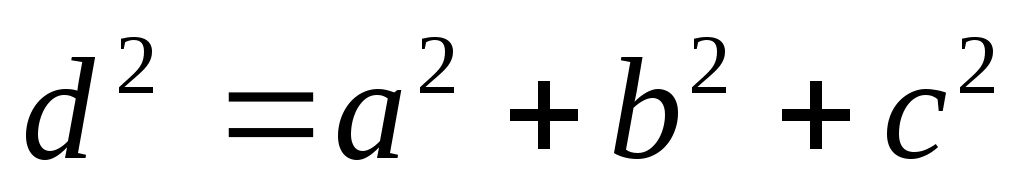
33-суретте параллелепипедтің диагоналдық қимасы берілген.
33-сурет
6.2. Кубтың және тікбұрышты параллелепипед беттерінің аудандары.
Біз куб пен тікбұрышты параллелепипедтің қасиеттері туралы біраз мағлұматпен таныспыз. Олардың жақтары – біз аудандарын жеңіл есептей білетін квадраттар немесе тіктөртбұрыштар.
Олардың бүйір беті мен толық бетін ажырата білу керек. Бүйір беті тек бүйір жақтарынан ғана тұрады, оған табандары кірмейді.
Табанының қырлары a, b және бүйір қыры c болатын тікбұрышты параллелепипедті қарастыралық (35-сурет). Ол призманың дербес түрі болғандықтан, 1, 2-теоремалардан мыналарды аламыз:
Sтік.пар.б.б.=(2a+2b)c=2(a+b)c,
Sтік пар.т.б=2(a+b)c+2ab7
Сонымен, тікбұрышты параллелепипедтің бүйір бетінің ауданы оның төрт бүйір жағының аудандарының қосындысына тең, ал толық беті оның бүйір бетінің ауданы мен екі еселенген табанының ауданының қосындысына тең.
Куб болғанда, b=c=a (36-сурет). Сондықтан,
Sкуб.б.б.=4a2, Sкуб.т.б.=6a2,
мұндағы а – куб қыры.
Тапсырмалар.
№36. Тікбұрышты параллелепипед қабырғаларының өлшемдері 4дм, 2дм және 4дм. Параллелепипедтің диагоналінің ұзындығын есептеңдер.
№37. Тікбұрышты параллелепипедтін өлшемдері 2см, 3см жөне 6см. Оның диагональдарының ұзындықтарын табыңдар.
№38. Параллелепипедтің өлшемдері 3см, 4см жөне 5см. Параллелепипед диагоналінің оның ең кіші жағымен жасайтын көлбеулік бұрышын табыңдар.
№39. Куб диагоналінің үзындығы 4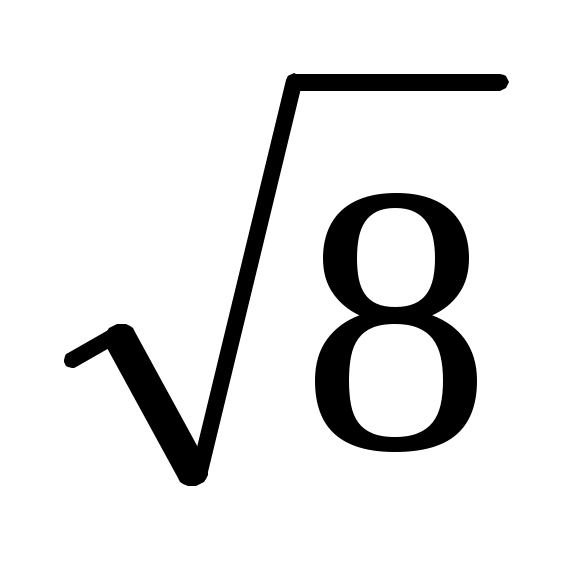
см. Куб кырының ұзындығын табыңдар.
№40. Егер кубтың қыры а) 4см; ә) 10см; б) 1м болса, оның толық бетінің ауданы неге тең?
№41. Егер кубтың қыры а) 6см, ә) 10см; б) 12см болса, оның бүйір бетінің және толық бетінің аудандары неге тең?
№42. Табанының қабырғалары 2см және 4 см-ге, биіктігі 2 см-ге тең тік бұрышты параллелепипед берілген. Параллелепипедтің бүйір бетінің және толық бетінің аудандарын табыңдар.
№43. Ағаш тақтайдың ұзындығы 6см, ені 24см, қалыңдығы 3см. Оның толық бетінің ауданын есептеңдер.
№44. Егер кубтың толык беті а) 150 см2; ө) 600 см2; б) 216 см2 болса, оның кырының ұзындығын есептеңдер.
№45. Егер кубтың бүйір бетінің ауданы а) 64 см2; ә) 324 см2; б) 576 см2 болса, кубтың толық бетінің ауданын есептеңдер.
№46. Тікбұрышты параллелепипедтің үш жағының аудандары 24дм2, 28дм2 және 42м2. Оның өлшемдерін табыңдар.
№47. Тік параллелепипедтің табанының диагональдары 0,6м жөне 0,8м-ге тең ромб болып табылады. Параллелепипедтің бүйір жағының диагоналі 1,3м. Оның толық бетін табыңдар.
№48. Тікбұрышты параллелепипедтің үш өлшемінің қатынасы 1:2:3, ал толық беті 198 дм2. Оның өлшемдерін табыңдар.
§7. Пирамида.
7.1. Пирамиданың анықтамасы және жалпы қасиеттері.
Көпжақтардың ерекше бір түрі – пирамида. Пирамида тақырыбын қозғағанда Мысыр пирамидаларын атамай кету мүмкін емес. Олар тек математиктерді ғана емес, сонымен қатар физиктерді, тарихшыларды, т.б. қызықтырып келеді. Оларды зерттеумен ғалымдар жүздеген ғасырлар бойы айналысуда. Сонымен пирамида дегеніміз не?
Алдымен пирамиданың ең қарапайым түрі – үшбұрышты пирамидаларды қарастыралық.
Пирамиданың табанында жатқан үшбұрыштың түріне қарай пирамида әртүрлі көрінуі мүмкін. Мысалы, 38.1-суретте тікбұрышты пирамида, ал 38.2-суретте ұшбұрышты көлбеу пирамида бейнеленген.
Бұл атаулар пирамиданың биіктігінің, дәлірек айтқанда, биіктігінің табаны қалай, қайда орналасқанымен байланысты. Пирамиданың биіктігі дегеніміз — оның төбесінен табан жазықтығына түсірілген перпендикуляр немесе осы перпендикулярдың ұзындығы.
Үшбүрышты пирамиданың биіктігін нүктеден жазықтыққа түсірілген перпендикуляр түсінігі арқылы анықтауға болады. 38.1-суреттен тік пирамида биіктігінің табаны пирамида табанының ішкі нүктесі болатынын көреміз. Көлбеу пирамида биіктігінің табаны пирамида табанынан тысқары жатыр (38.2-сурет).
38.3-суретте дұрыс үшбүрышты пирамида бейнеленген. Ондай пирамиданың табанында дұрыс үшбүрыш жатады, ал оның барлық бүйір жақтары өзара тең болатын теңбүйірлі үшбұрыштар болып табылады. Бұл жағдайда биіктіктің табаны пирамида табанының центріне дәл түседі (табанының центрін табанының төбелерінен бірдей қашықтықта орналасқан нүкте ретінде анықтауға болады).
Геометрияда барлық жақтары теңқабырғалы үшбұрыштар болатын пирамиданың дербес түрі жиі карастырылады. Мұндай пирамидаларды тетраэдрлер деп атайды. Ол "төртжақты" деген мағына білдіреді.
Үшбұрышты пирамидалар (жазықтықтағы үшбұрыштар тәрізді) қатаңдық касиетіне ие. Пирамидалар — "қатаң" геометриялық фигуралар, басқаша айтқанда, олардың пішінін өзгертуге болмайды.
Жалпы жағдайда пирамиданың түрін оның табанында жататын көпбұрыш анықтайды. Сондықтан пирамидалар төртбұрышты, бесбұрышты, жетібұрышты тіпті п бұрышты да болуы мүмкін. Егер оның табанында п бұрыш жатса, онда пирамида п бұрышты деп аталады.
Анықтама. Пирамида деп бір жагы кез келген көпбұрыш, ал қалган жақтары төбелері ортақ ушбұрыштардан тұратын көпжақты атайды.
39-суретте табандары көпбұрыштар болатын әртүрлі пирамидалар бейнеленген. Пирамидаларды дөңес және дөңес емес деп бөлеміз.
Үшбұрышты пирамидалар (40-сурет) әрқашан дөңес көпжақтарға жатады. Ал басқа пирамидалардың дөңес емес болуы да мүмкін. 41-суретте дөңес емес SАВСD төртбұрышты пирамида бейнеленген. Оны кез келген жағымен жазықтыққа жатқызуға келмейді.
Егер біз "пирамида" деп жазсақ (немесе айтсақ), онда әңгіме дөңес пирамида туралы болып тұр деп түсінуіміз керек.
Анықтама. Егер пирамиданың табаны дұрыс көпбұрыш болып, төбесінің проекциясы табанының центріне дәл түссе, онда ол дұрыс пирамида деп аталады. (42-сурет).
42-суретте дұрыс алтыбұрышты пирамида бейнеленген.
Дұрыс пирамиданың бүйір жағының пирамида тпөбесінен түсірілген биіктігі пирамиданың апофемасы деп аталады.
Мысалы, 42-суретте ҒК—пирамиданың апофемасы.
Дұрыс пирамиданың
• бүйір қырларының тең екенін;
• бүйір жақтарының тең екенін;
• апофемаларының тең екенін;
• табанындағы екіжақты бұрыштарының тең екенін;
• бүйір қырларындағы екіжақты бұрыштарының тең екенін дәлелдеуге болады.
7.2. Пирамида бетінің ауданы
Анықтама. Пирамиданың буйір бетініц ауданы Sпир.б.б деп оның барлық бүйір жақтарының аудандарының қосындысын айтады. Толық бетінің ауданы оның барлық жақтарының аудандарының цосындысына тең.
Яғни Sпир.т.б=Sпир.б.б+Sтаб, мұндағы Sтаб – табанының ауданы.
Теорема. Пирамиданың бүйір бетінің ауданы оның табанының периметрінің жартысын пирамиданың апофемасына көбейткенге тең.
Sпир.б.б=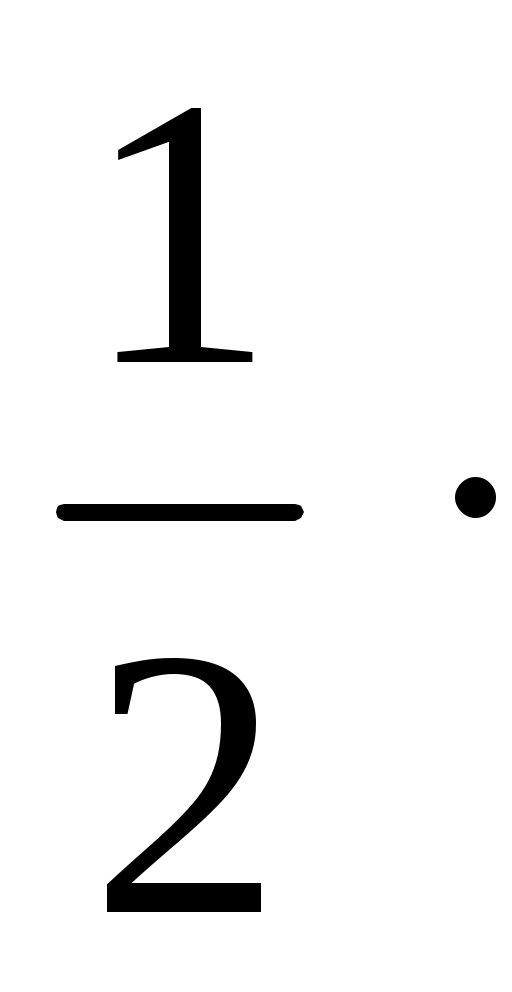
Pk, мұндағы k – пирамида апофемасы.
Тапсырмалар.
№49. Пирамиданың табаны — диагоналі 10 см-ге тең тіктөртбұрыш. Пирамиданың әрбір бүйір кыры 13см. Пирамиданың биіктігін табыңдар.
№50. Пирамиданың әрбір бүйір қыры 17см-ге тең, ал табаны — қабырғалары 18см және 24см болатын тіктөртбұрыш. Пирамиданың биіктігін табыңдар.
№51. Пирамиданың табаны — кабырғасы 6см-ге тең теңқабырғалы үшбұрыш. Пирамиданың әрбір бүйір қыры табан жазықтығымен 45° бұрыш жасайды. Пирамиданың биіктігін табыңдар.
№52. Төртбұрышты дұрыс пирамиданың биіктігі 7см-ге тең, ал табан қабырғасы 8см. Бүйір қырын табыңдар.
№53. Пирамиданың табаны — қабыргалары 12см және 10см болатын тіктөртбұрыш. Пирамиданың ұзындығы 8см-ге тең биіктігінің табаны тіктөрт-бұрыштың диагональдарының қиылысу нүктесі болып табылады. а) Пира-миданың бүйір бетінің ауданын; ә) пирамиданың толық бетінің ауданын табыңдар.
№54. Пирамиданың табаны — теңбүйірлі үшбұрыш. Үшбұрыштың биіктігі 12дм, ал табаны 8дм. Пирамиданың әрбір бүйір кыры 15дм. Пирамиданың биіктігін табындар.
№55. Пирамиданың табаны — тіктөртбұрыш. Оның қабырғалары 0,6дм, 0,8дм. Пирамиданың әрбір бүйір кыры 1,5дм. Пирамиданың биіктігін табыңдар.
№56. Дұрыс төртбұрышты пирамиданың табанының ауданы 36см2. Бүйір қыры 5см. Пирамиданың апофемасын және бүйір бетінің ауданын табыңдар.
№57. Дұрыс төртбұрышты пирамиданың толық бетінің ауданы 84дм2, ал табанының ауданы 36дм2. Пирамиданың а) табанының қабырғасын; ә) апофе-масын; б) бүйір қырын табыңдар.
№58. Дұрыс төртбұрышты пирамиданың табанының қабырғасы 10дм, ал бүйір қыры 13дм. Оның биіктігінің ортасы арқылы табанына параллель қиюшы жазыктық жүргізілген. Қиманын ауданын табыңдар.
№59. Дұрыс үшбүрышты пирамиданың табанының қабырғасы 12дм, биіктігі 10дм. Пирамиданың бүйір кабырғасының ортасы арқылы табанына параллель қиюшы жазыктық жүргізілген. Қиманың ауданын табыңдар.
№60. Дұрыс үшбұрышты пирамиданың табанының қабырғасы 10дм, ал бүйір қабырғасы табан жазықтығымен 45° бұрыш жасайды. Пирамиданың бүйір бетінің ауданын табыңдар.
№61. Пирамиданың биіктігі 12м. Табанының ауданы 576м2. Егер параллель қиманың ауданы 64м2 болса, қима пирамида табанынан қандай кашықтықта өтеді?
№62. Пирамиданың табаны — диагональдары 6см және 8см болатын ромб. Пирамиданың биіктігі ромб диагональдарының қиылысу нүктесі арқылы өтеді және 3см-ге тең. Диагональдық қималардың аудандарын табыңдар.
№63. Дұрыс алтыбұрышты пирамиданың табанының қабырғасы 8см, бүйір қыры табан жазықтығымен 45° бұрыш жасайды. Диагональдық қималардың аудандарын табыңдар.
§8. Қиық пирамида және оның бетінің ауданы.
Анықтама. Пирамиданың табаны мен табан жазықтығына параллелъ қима жазықтыгының арасындагы бөлігі қиық пирамида деп аталады (52.1-сурет).
Мысалы, АВСDЕА1.В1С1D1.Е1 көпжағы — бесбұрышты киық пирамида (52.2-сурет). Қиық пирамиданың төменгі (АВСDЕ көпбұрышы) және жоғарғы (А1В1С1D1.Е1 көпбұрышы) екі табаны бар. Қиык пирамидаңың бүйір жақтары — трапециялар, ал оның бүйір кырлары — осы трапециялардың бүйір қабырғалары.
Бір табанының кез келген нүктесінен екінші табан жазықтығына түсірілген перпендикуляр қиық пирамиданың биіктігі деп аталады. 52.2-суреттегі О1О кесіндісін қиық пирамиданың биіктігі, ал оның ұзындығын табандарының арақашықтығы деп атауға да болады.
6.1. Параллелепипедтің анықтамасы.
Анықтама. Табандары параллелограмдар болатын призманы параллелепипед деп атайды (27-сурет).
Қарама-қарсы жақтарының үш жұбының қай-қайсысын да табандары ретінде ала беруге болады.
Паралелепипедке төрт диагональ жүргізуге болады. 28-суретте ABCDA1B1C1D1 параллелепипедінің диагональдары – AC1, BD1, CA1, DB1.
Анықтама. Барлық жақтары тіктөртбұрыш болатын параллелепипедті тікбұрышты параллелепипед деп атайды (29-сурет).
Тікбұрышты параллелепипедтің бір төбесінен шығатын үш қырының ұзындығы оның өлшемдері деп аталады. 30.1-суретте өлшемдері a, b, c болатын тікбұрышты параллелепипед бейнеленген.
Барлық өлшемдері тең тікбұрышты параллелепипед куб деп аталады (30.2-сурет). Кубтың барлық жақтары квадраттар.
Теорема. Тікбұрышты параллелепипедтің диагоналінің квадраты, оның бір төбесінен шығатын қабырғаларының квадраттарының қосындысына тең (32-сурет).
33-суретте параллелепипедтің диагоналдық қимасы берілген.
33-сурет
6.2. Кубтың және тікбұрышты параллелепипед беттерінің аудандары.
Біз куб пен тікбұрышты параллелепипедтің қасиеттері туралы біраз мағлұматпен таныспыз. Олардың жақтары – біз аудандарын жеңіл есептей білетін квадраттар немесе тіктөртбұрыштар.
Олардың бүйір беті мен толық бетін ажырата білу керек. Бүйір беті тек бүйір жақтарынан ғана тұрады, оған табандары кірмейді.
Табанының қырлары a, b және бүйір қыры c болатын тікбұрышты параллелепипедті қарастыралық (35-сурет). Ол призманың дербес түрі болғандықтан, 1, 2-теоремалардан мыналарды аламыз:
Sтік.пар.б.б.=(2a+2b)c=2(a+b)c,
Sтік пар.т.б=2(a+b)c+2ab7
Сонымен, тікбұрышты параллелепипедтің бүйір бетінің ауданы оның төрт бүйір жағының аудандарының қосындысына тең, ал толық беті оның бүйір бетінің ауданы мен екі еселенген табанының ауданының қосындысына тең.
Куб болғанда, b=c=a (36-сурет). Сондықтан,
Sкуб.б.б.=4a2, Sкуб.т.б.=6a2,
мұндағы а – куб қыры.
Тапсырмалар.
№36. Тікбұрышты параллелепипед қабырғаларының өлшемдері 4дм, 2дм және 4дм. Параллелепипедтің диагоналінің ұзындығын есептеңдер.
№37. Тікбұрышты параллелепипедтін өлшемдері 2см, 3см жөне 6см. Оның диагональдарының ұзындықтарын табыңдар.
№38. Параллелепипедтің өлшемдері 3см, 4см жөне 5см. Параллелепипед диагоналінің оның ең кіші жағымен жасайтын көлбеулік бұрышын табыңдар.
№39. Куб диагоналінің үзындығы 4
см. Куб кырының ұзындығын табыңдар.№40. Егер кубтың қыры а) 4см; ә) 10см; б) 1м болса, оның толық бетінің ауданы неге тең?
№41. Егер кубтың қыры а) 6см, ә) 10см; б) 12см болса, оның бүйір бетінің және толық бетінің аудандары неге тең?
№42. Табанының қабырғалары 2см және 4 см-ге, биіктігі 2 см-ге тең тік бұрышты параллелепипед берілген. Параллелепипедтің бүйір бетінің және толық бетінің аудандарын табыңдар.
№43. Ағаш тақтайдың ұзындығы 6см, ені 24см, қалыңдығы 3см. Оның толық бетінің ауданын есептеңдер.
№44. Егер кубтың толык беті а) 150 см2; ө) 600 см2; б) 216 см2 болса, оның кырының ұзындығын есептеңдер.
№45. Егер кубтың бүйір бетінің ауданы а) 64 см2; ә) 324 см2; б) 576 см2 болса, кубтың толық бетінің ауданын есептеңдер.
№46. Тікбұрышты параллелепипедтің үш жағының аудандары 24дм2, 28дм2 және 42м2. Оның өлшемдерін табыңдар.
№47. Тік параллелепипедтің табанының диагональдары 0,6м жөне 0,8м-ге тең ромб болып табылады. Параллелепипедтің бүйір жағының диагоналі 1,3м. Оның толық бетін табыңдар.
№48. Тікбұрышты параллелепипедтің үш өлшемінің қатынасы 1:2:3, ал толық беті 198 дм2. Оның өлшемдерін табыңдар.
§7. Пирамида.
7.1. Пирамиданың анықтамасы және жалпы қасиеттері.
Көпжақтардың ерекше бір түрі – пирамида. Пирамида тақырыбын қозғағанда Мысыр пирамидаларын атамай кету мүмкін емес. Олар тек математиктерді ғана емес, сонымен қатар физиктерді, тарихшыларды, т.б. қызықтырып келеді. Оларды зерттеумен ғалымдар жүздеген ғасырлар бойы айналысуда. Сонымен пирамида дегеніміз не?
Алдымен пирамиданың ең қарапайым түрі – үшбұрышты пирамидаларды қарастыралық.
| 37-суретте О, А, В және С төбелерімен берілген ОАВС үшбұрышты пирамидасы бейнеленген. О нүктесі пирамиданың төбесі деп аталады. Пирамиданың ОАВ, ОВС, ОСА, АВС жақтары – үшбұрыштар. АВС жағын пирамиданың табаны деп атайды. ОА, ОВ, ОС, АВ, ВС АС кесінділері – пирамиданың қырлары. |  |
Пирамиданың табанында жатқан үшбұрыштың түріне қарай пирамида әртүрлі көрінуі мүмкін. Мысалы, 38.1-суретте тікбұрышты пирамида, ал 38.2-суретте ұшбұрышты көлбеу пирамида бейнеленген.
Бұл атаулар пирамиданың биіктігінің, дәлірек айтқанда, биіктігінің табаны қалай, қайда орналасқанымен байланысты. Пирамиданың биіктігі дегеніміз — оның төбесінен табан жазықтығына түсірілген перпендикуляр немесе осы перпендикулярдың ұзындығы.
Үшбүрышты пирамиданың биіктігін нүктеден жазықтыққа түсірілген перпендикуляр түсінігі арқылы анықтауға болады. 38.1-суреттен тік пирамида биіктігінің табаны пирамида табанының ішкі нүктесі болатынын көреміз. Көлбеу пирамида биіктігінің табаны пирамида табанынан тысқары жатыр (38.2-сурет).
38.3-суретте дұрыс үшбүрышты пирамида бейнеленген. Ондай пирамиданың табанында дұрыс үшбүрыш жатады, ал оның барлық бүйір жақтары өзара тең болатын теңбүйірлі үшбұрыштар болып табылады. Бұл жағдайда биіктіктің табаны пирамида табанының центріне дәл түседі (табанының центрін табанының төбелерінен бірдей қашықтықта орналасқан нүкте ретінде анықтауға болады).
Геометрияда барлық жақтары теңқабырғалы үшбұрыштар болатын пирамиданың дербес түрі жиі карастырылады. Мұндай пирамидаларды тетраэдрлер деп атайды. Ол "төртжақты" деген мағына білдіреді.
Үшбұрышты пирамидалар (жазықтықтағы үшбұрыштар тәрізді) қатаңдық касиетіне ие. Пирамидалар — "қатаң" геометриялық фигуралар, басқаша айтқанда, олардың пішінін өзгертуге болмайды.
Жалпы жағдайда пирамиданың түрін оның табанында жататын көпбұрыш анықтайды. Сондықтан пирамидалар төртбұрышты, бесбұрышты, жетібұрышты тіпті п бұрышты да болуы мүмкін. Егер оның табанында п бұрыш жатса, онда пирамида п бұрышты деп аталады.
Анықтама. Пирамида деп бір жагы кез келген көпбұрыш, ал қалган жақтары төбелері ортақ ушбұрыштардан тұратын көпжақты атайды.
39-суретте табандары көпбұрыштар болатын әртүрлі пирамидалар бейнеленген. Пирамидаларды дөңес және дөңес емес деп бөлеміз.
Үшбұрышты пирамидалар (40-сурет) әрқашан дөңес көпжақтарға жатады. Ал басқа пирамидалардың дөңес емес болуы да мүмкін. 41-суретте дөңес емес SАВСD төртбұрышты пирамида бейнеленген. Оны кез келген жағымен жазықтыққа жатқызуға келмейді.
Егер біз "пирамида" деп жазсақ (немесе айтсақ), онда әңгіме дөңес пирамида туралы болып тұр деп түсінуіміз керек.
Анықтама. Егер пирамиданың табаны дұрыс көпбұрыш болып, төбесінің проекциясы табанының центріне дәл түссе, онда ол дұрыс пирамида деп аталады. (42-сурет).
42-суретте дұрыс алтыбұрышты пирамида бейнеленген.
Дұрыс пирамиданың бүйір жағының пирамида тпөбесінен түсірілген биіктігі пирамиданың апофемасы деп аталады.
 | |
Мысалы, 42-суретте ҒК—пирамиданың апофемасы.
Дұрыс пирамиданың
• бүйір қырларының тең екенін;
• бүйір жақтарының тең екенін;
• апофемаларының тең екенін;
• табанындағы екіжақты бұрыштарының тең екенін;
• бүйір қырларындағы екіжақты бұрыштарының тең екенін дәлелдеуге болады.
7.2. Пирамида бетінің ауданы
Анықтама. Пирамиданың буйір бетініц ауданы Sпир.б.б деп оның барлық бүйір жақтарының аудандарының қосындысын айтады. Толық бетінің ауданы оның барлық жақтарының аудандарының цосындысына тең.
Яғни Sпир.т.б=Sпир.б.б+Sтаб, мұндағы Sтаб – табанының ауданы.
Теорема. Пирамиданың бүйір бетінің ауданы оның табанының периметрінің жартысын пирамиданың апофемасына көбейткенге тең.
Sпир.б.б=
Pk, мұндағы k – пирамида апофемасы.Тапсырмалар.
№49. Пирамиданың табаны — диагоналі 10 см-ге тең тіктөртбұрыш. Пирамиданың әрбір бүйір кыры 13см. Пирамиданың биіктігін табыңдар.
№50. Пирамиданың әрбір бүйір қыры 17см-ге тең, ал табаны — қабырғалары 18см және 24см болатын тіктөртбұрыш. Пирамиданың биіктігін табыңдар.
№51. Пирамиданың табаны — кабырғасы 6см-ге тең теңқабырғалы үшбұрыш. Пирамиданың әрбір бүйір қыры табан жазықтығымен 45° бұрыш жасайды. Пирамиданың биіктігін табыңдар.
№52. Төртбұрышты дұрыс пирамиданың биіктігі 7см-ге тең, ал табан қабырғасы 8см. Бүйір қырын табыңдар.
№53. Пирамиданың табаны — қабыргалары 12см және 10см болатын тіктөртбұрыш. Пирамиданың ұзындығы 8см-ге тең биіктігінің табаны тіктөрт-бұрыштың диагональдарының қиылысу нүктесі болып табылады. а) Пира-миданың бүйір бетінің ауданын; ә) пирамиданың толық бетінің ауданын табыңдар.
№54. Пирамиданың табаны — теңбүйірлі үшбұрыш. Үшбұрыштың биіктігі 12дм, ал табаны 8дм. Пирамиданың әрбір бүйір кыры 15дм. Пирамиданың биіктігін табындар.
№55. Пирамиданың табаны — тіктөртбұрыш. Оның қабырғалары 0,6дм, 0,8дм. Пирамиданың әрбір бүйір кыры 1,5дм. Пирамиданың биіктігін табыңдар.
№56. Дұрыс төртбұрышты пирамиданың табанының ауданы 36см2. Бүйір қыры 5см. Пирамиданың апофемасын және бүйір бетінің ауданын табыңдар.
№57. Дұрыс төртбұрышты пирамиданың толық бетінің ауданы 84дм2, ал табанының ауданы 36дм2. Пирамиданың а) табанының қабырғасын; ә) апофе-масын; б) бүйір қырын табыңдар.
№58. Дұрыс төртбұрышты пирамиданың табанының қабырғасы 10дм, ал бүйір қыры 13дм. Оның биіктігінің ортасы арқылы табанына параллель қиюшы жазыктық жүргізілген. Қиманын ауданын табыңдар.
№59. Дұрыс үшбүрышты пирамиданың табанының қабырғасы 12дм, биіктігі 10дм. Пирамиданың бүйір кабырғасының ортасы арқылы табанына параллель қиюшы жазыктық жүргізілген. Қиманың ауданын табыңдар.
№60. Дұрыс үшбұрышты пирамиданың табанының қабырғасы 10дм, ал бүйір қабырғасы табан жазықтығымен 45° бұрыш жасайды. Пирамиданың бүйір бетінің ауданын табыңдар.
№61. Пирамиданың биіктігі 12м. Табанының ауданы 576м2. Егер параллель қиманың ауданы 64м2 болса, қима пирамида табанынан қандай кашықтықта өтеді?
№62. Пирамиданың табаны — диагональдары 6см және 8см болатын ромб. Пирамиданың биіктігі ромб диагональдарының қиылысу нүктесі арқылы өтеді және 3см-ге тең. Диагональдық қималардың аудандарын табыңдар.
№63. Дұрыс алтыбұрышты пирамиданың табанының қабырғасы 8см, бүйір қыры табан жазықтығымен 45° бұрыш жасайды. Диагональдық қималардың аудандарын табыңдар.
§8. Қиық пирамида және оның бетінің ауданы.
Анықтама. Пирамиданың табаны мен табан жазықтығына параллелъ қима жазықтыгының арасындагы бөлігі қиық пирамида деп аталады (52.1-сурет).
Мысалы, АВСDЕА1.В1С1D1.Е1 көпжағы — бесбұрышты киық пирамида (52.2-сурет). Қиық пирамиданың төменгі (АВСDЕ көпбұрышы) және жоғарғы (А1В1С1D1.Е1 көпбұрышы) екі табаны бар. Қиык пирамидаңың бүйір жақтары — трапециялар, ал оның бүйір кырлары — осы трапециялардың бүйір қабырғалары.
Бір табанының кез келген нүктесінен екінші табан жазықтығына түсірілген перпендикуляр қиық пирамиданың биіктігі деп аталады. 52.2-суреттегі О1О кесіндісін қиық пирамиданың биіктігі, ал оның ұзындығын табандарының арақашықтығы деп атауға да болады.