Файл: Приднестровский Государственный Университет им. Т. Г. Шевченко Инженернотехнический институт.docx

При средней твердости шестерни НВ₁ = 229 базовое число циклов нагружения N_{HG 1}= 1,42 (·10⁷),

а для колеса при НВ₂ =208 базовое число циклов нагружения

N_{HG 2=} 1,12 (·10⁷) (интерполированием) (табл. 3).

Таблица 3

Средняя твердость поверхности зубьев	НВср HRC	< 200 –	250 27	300 33	350 38	– 40	– 45	– 50	– 55
NHG циклов (·107)		1,0	1,7	2,5	3,6	4,4	6,0	8,0	10

Поскольку N_{HЕ 2} > N_{HG 2} и N_{HЕ 1} > N_HG1, то 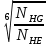= 1
12. Предел контактной выносливости для колеса:

σ_{Н lim2} = 2НВ₂ + 70 =2∙208+70=486 МПа

Допускаемое контактное напряжение для колеса:

принимая коэффициент безопасности S_H =1,1;


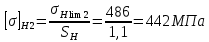
Предел контактной выносливости для шестерни:

σ_{Н lim1} = 2НВ₁ + 70 = 2∙229,5+70=529 МПа

Допускаемое контактное напряжение для шестерни:

принимая коэффициент безопасности S_H =1,1


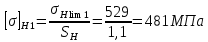
За расчетное допускаемое контактное напряжение в косозубых передачах принимается

[σ]_Н = 0,45· ( [σ]_Н1+[σ]_Н2 ) =0,45∙(481+442)=415 МПа


13. Межосевое расстояние для прямозубой передачи.

Принимая предварительно К_Н = 1,3 и задаваясь значениями

ψ_ba = 0,4 и ψ_ba = 0,5 находим два значения a_w по формуле:








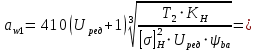
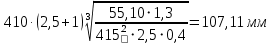
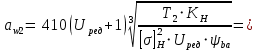
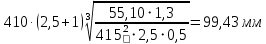
Одно из найденных межосевых расстояний 99,43 мм округляем до ближайшего стандартного значения из следующего ряда

---

a_{w сm} = … 80;90;100;112;125;140;160;180;200… мм.
14. Ширина зубчатых колес:

b₂ = 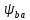∙ a_{w ст} =0,5∙100=50 мм

b₁ = b₂ + 5 мм =50+5=55 мм
15. Модуль передачи:

0,01 ∙ a_{w ст} < т_n < 0,02 ∙ a_{w ст} , мм

0,01 ∙ 100 < т_n < 0,02 ∙ 100, мм

1,00 < т_n < 2,00 мм

Рекомендуется принимать значение модуля т_{n ст}=2 мм (или т_{n ст}=1 мм).

Принимаем т_{n ст} = 2 мм
16. Суммарное число зубьев косозубой передачи (предварительно принимая β’ = 12˚ и cos12˚ = 0,9781):



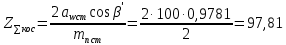
округлив до целого числа, принимаем: Z_∑кос =98

Действительное значение угла наклона зубьев:



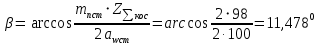
β = 11,478⁰ при [β]= 8˚…15˚

Значения β не округлять!
Осевой шаг:

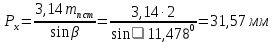при b₂ = 50 мм

должно быть Р_х < b_2- условие выполнено
17. Число зубьев шестерни:

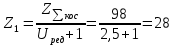округлив до целого числа,
принимаем Z₁ = 28

при Z_1minкос= 17cos³ 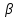= 17cos³11,478⁰ = 16,0

Z₁ > Z_{1min кос} 32> 16,0
18. Число зубьев колеса:

Z₂ = Z_∑кос – Z₁ =98-28=70
19. Уточнение передаточного числа:



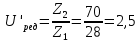
Отклонение от принятого ранее передаточного числа:



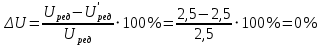
что находится в пределах допустимого [∆U] = ±4%.

20. Геометрические размеры колес.

Делительный диаметр шестерни:

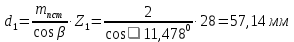-значение d₁ не округлять

Делительный диаметр колеса:

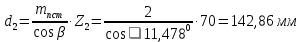-значение d₂

---

не округлять

Межосевое расстояние:



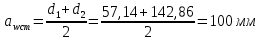
Диаметр вершин зубьев шестерни:

d_a1 = d₁ + 2m_ncт = 57,14+2∙2=61,14 мм

Диаметр вершин зубьев колеса:

d_a2 = d₂ + 2 m_ncm=142,86+2∙2=146,86 мм
Диаметр впадин зубьев шестерни:

d_f1 = d₁ – 2,5m_ncт = 57,14-2,5∙2=52,14 мм

Диаметр впадин зубьев колеса:

d_f2 = d₂ – 2,5m_{n ст} = 142,86-2,5∙2=137,86 мм
21. Проверочный расчет на контактную прочность:



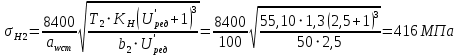
Отклонение от [σ]_Н2 :

∆σ% =

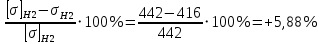
при допускаемом отклонении –5% <[∆σ] <15%.

Условие прочности выполняется.
22. Проверка зубьев на изгиб.

Эквивалентное время работы передачи в сутки при расчете изгиб:

.

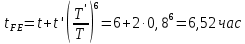23. Эквивалентное время работы передачи в течение всего срока службы:

T_FЕ = t_FЕ ∙ д ∙ L =6,52∙260∙5=8476 час,

где число рабочих дней в году д=260 дн. и срок службы передачи L=5 лет.
24. Эквивалентное число циклов нагружения зубьев колеса:

N_{FЕ 2} = 60 ∙ п₂ ∙ Т_FЕ = 60∙564∙8476=286 827 840 циклов

Таким образом, передача работает при постоянной нагрузке, т.к.

N_{FЕ 2} > N_FG 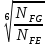= 1
25. Допускаемые напряжения изгиба [σ]_F:

Предел изгибной выносливости для зубьев шестерни σ_{Flim 1} :

σ_{Flim 1} = 1,8 ∙ НВ₁ =1,8∙229,5=413,1 МПа
Предел изгибной выносливости для зубьев колеса σ_Flim2:

σ_{Flim 2} = 1,8 ∙ НВ₂ =1,8∙208=374,4 МПа

где НВ₁ и НВ₂ см. п.11 расчета
Допускаемые напряжения изгиба для шестерни:



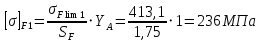
где коэффициент безопасности S_F = 1,75, а коэффициент

режима работы для нереверсивной передачи Y_A = 1.

---

Допускаемые напряжения изгиба для колеса:


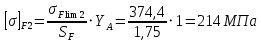
26. Окружное усилие на колесе:



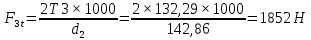
(где Т₃ Нм, см. п.7, аd₂ мм – см. п.20 расчета)
27. Коэффициент формы зубьев при расчете на изгиб по местным напряжениям Y_FS для косозубых передач определяют в зависимости от Z_V (из табл. 4):





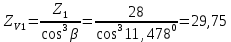
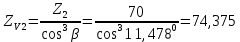
У_FS1 =3,8 (при Z_V1=29,75 ≈30)

У_FS2 = 3,61 (при Z_V2=74,375≈80)

Таблица 4

Значения коэффициента Y_FS в зависимости от Z или Z_V

Zили Zv	17	18	19	20	21	22	23	24	25	26
YFS	4,28	4,23	4,15	4,09	4,05	4,01	3,97	3,93	3,9	3,88

Z или Zv	27	28	29	30	40	50	60	80	100 и более
YFS	3,86	3,84	3,82	3,8	3,7	3,66	3,62	3,61	3,6

Расчет на изгиб производится для той зубчатки, у которой отношение 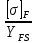меньше.

Для шестерни:

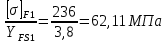
Для колеса:

---

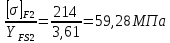
Для колеса это отношение меньше, поэтому расчет ведем по зубу колеса.

Коэффициент нагрузки при расчете на изгиб предварительно принимаем
К_F = 1,3
Коэффициент торцового перекрытия 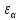определяется:

=

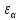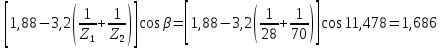
Коэффициент повышения прочности зубьев косозубых передач по напряжениям изгиба Y_Fβ определяется:



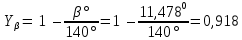
(где 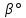=11,478⁰ см. п.16 расчета)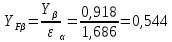


Напряжение изгиба для зубьев колеса:



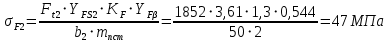
Внимание! Размеры b₂ и m_cmподставляются в мм!

Поскольку σ_F2 = 47 МПа < [σ]_F2 = 2140 МПа, то условие прочности выполняется.
28. Расчет на кратковременные перегрузки.

• 
  _{По контактным напряжениям}
  

Максимальное допускаемое контактное напряжение при пусковой перегрузке:

[σ] _{Н max2} = 2,8 ∙ σ_т =2,8∙395=1106 МПа

где σ_т=395 МПа для материала колеса (см. п.10 расчета)



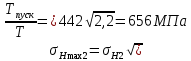
Где σ_Н2 =442 МПа (см п.21 расчета)

Поскольку σ_{Н max2} =656 МПа <[σ]_{Н max2} = 1106Мпа, то условие прочности выполняется.

• 
  По напряжениям изгиба
  

Максимальное допускаемое напряжение изгиба при пусковой

перегрузке:

[σ]_{F max2} = 2,74 ∙ НВ₂ =2,74∙208=570 МПа,

где НВ₂ =208 МПа (см п.11 расчета)

Максимальное напряжение изгиба при пусковой перегрузке:



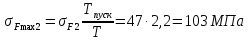
отношение 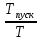дано в задании, а σ_F2 см п.27 расчета.

Поскольку σ_{F max2} =103МПа < [σ]

---