Файл: Расчетнографическая работа по дисциплине механика.docx

Подставим Error: Reference source not found в Error: Reference source not found и запишем:

.

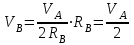(4.14)

Итоговые соотношения для скоростей тел механической системы

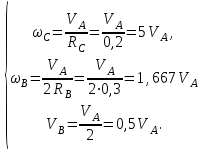(4.05)

Рассчитаем для заданных исходных данных скорости всех тел:

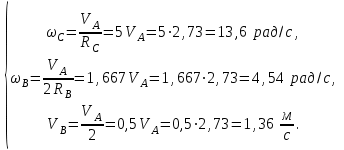(4.16)

4.3. Определение ускорений тел механической системы

Для определения ускорений дифференцируем выражения для скоростей

.

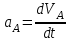(4.07)

Для определения значений ускорений остальных тел механической системы продифференцируем выражения Error: Reference source not found по времени и получим: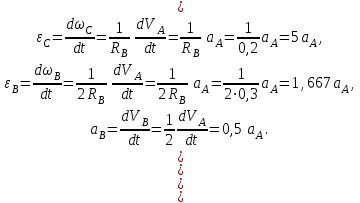

(4.08)

На рис. 4.3 изобразим ускорения всех тел механической системы при заданном ускорении тела .

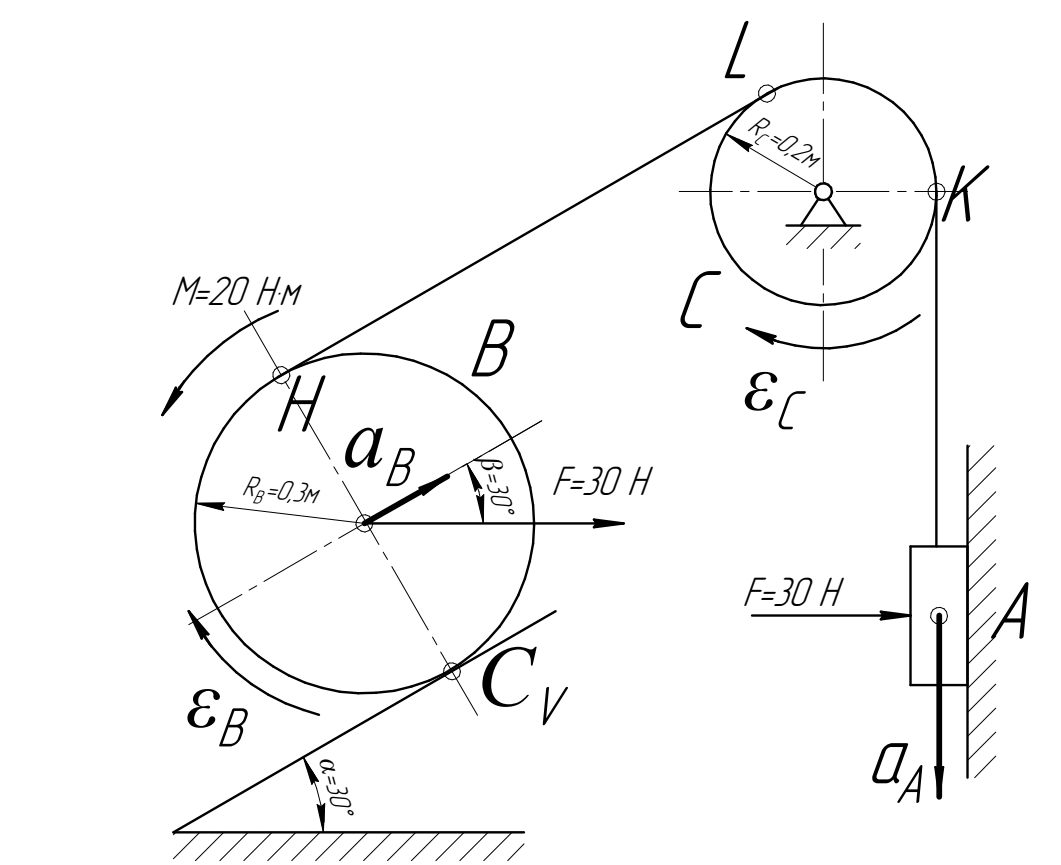Рис. 4.3. Ускорения тел механической системы

Окончательно на основе Error: Reference source not found запишем

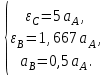(4.19)

Рассчитаем для заданных исходных данных ускорения всех тел:

---

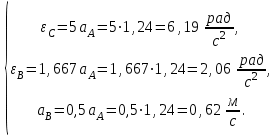(4.20)

---

Задача 5.

Применение теоремы об изменении кинетической энергии к изучению движения механической системы

5.1. Условие задачи

Механическая система (рисунок 5.1) под действием заданных сил и моментов, действующих на ее элементы, из состояния покоя приводится в движение так, что колесо В катится по плоскости. Массы элементов системы m_A, m_B, углы α и β, момент M, действующие силы F, радиусы колеса B и его радиус инерции ρ_B, приведены в таблице 2.1. Масса шкива С равна 5 кг, его радиус равен R_C = 0,2 м. Коэффициент трения скольжения тела А по поверхности равен f=0,1; коэффициент трения качения колеса В равен f_K=0,05R_B.

Считая, что шкив С представляет собой сплошной однородный диск, а гибкие связи невесомые и нерастяжимые, определить для заданной механической системы скорости, перемещения и ускорения всех тел, при найденной скорости , заданном перемещении метра и найденном ускорении тела , перемещающегося по вертикальной поверхности (рис. 5.1). Также необходимо определить натяжение нитей на всех участках.

Рис. 5.1. Механическая система при плоском движении (вариант 12)

Исходные данные:

---

Здесь ‒ массы тел механической системы.

5.2. Теорема об изменении кинетической энергии механической
системы

Задачу решаем на основе теоремы об изменении кинетической энергии механической системы.

Данная теорема имеет следующую формулировку:

«Изменение кинетической энергии механической системы на некоторое ее перемещение равно сумме работ внешних и внутренних сил, действующих на систему на том же перемещении».

Теорема записывается следующей формулой:

,

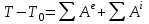(5.0)

где 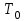‒ кинетическая энергия системы в начальном состоянии для начального момента времени;

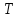‒ кинетическая энергия системы в конечном состоянии для конечного момента времени;

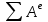‒ сумма работ всех внешних сил, действующих на рассматриваемую механическую систему;

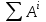‒ сумма работ всех внутренних сил.

Так как механическая система состоит из твердых тел и недеформируемых нитей, то сумма работ внутренних сил равна нулю:

.

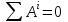(5.0)

Движение системы начинается из состояния покоя, поэтому кинетическая энергия системы в начальный момент времени равна нулю

.

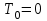(5.0)

При условиях (5.0) и (5.0) уравнение (5.0) принимает вид

.

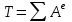(5.0)

Кинетическая энергия системы определяется как сумма кинетических энергий всех тел, входящих в систему

.

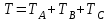(5.0)

---

5.3. Определение кинетической энергии механической системы

Для определения кинетической энергии механической системы необходимо знать скорости тел.

На данном этапе мы, как правило, не знаем не только значения скоростей, но и не знаем направление движения тел.

Поэтому на основе интуиции выбираем предполагаемое направление движения механической системы и изображаем для него скорости всех тел (рис. 5.2). В данном случае воспользуемся вариантом движения системы из задачи 4, показанном на рис. 5.2. Будем считать, что при заданных исходных данных тело будет двигаться вниз по вертикальной плоскости.

Рис. 5.2. Скорости тел механической системы

В дальнейшем при решении задачи выяснится насколько верно мы указали направления движения тел. Если направления движения выбрано не верно, то потребуется лишь поменять направление скоростей на противоположное, но при этом вычисления менять не придется, так как при определении кинетической энергии значения скоростей везде возводятся в квадрат.

Тело совершает поступательное движение со скоростью и его кинетическая энергия определяется формулой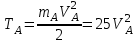

,

(5.0)

где 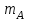‒ масса тела .

Тело совершает вращательное движение с угловой скоростью относительно неподвижного центра . Его кинетическая энергия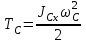

,

(5.0)

---