Файл: Учебное пособие соответствует рабочей программе дисциплины Строительная механика.docx

1.5. Степень свободы и степень изменяемости стержневых систем

Изменяемость внутренней структуры и подвижность сооружения относительно основания характеризуется его степенью свободы.

Свобода системы –это её возможность совершать какие-либо движения относительно земли без деформации элементов.

Степенью свободы системы W называется число независимых геометрических параметров, полностью определяющих положение системы относительно земли.

Если перемещения возникают в результате деформации элементов системы, то для определения положения в общем случае бесконечно большого числа точек объекта могут служить изменения (приращения) их координат при переходе из исходного положения в деформированное состояние. этих геометрических параметров, выступающих в качестве степеней свободы, получается бесконечное множество. Отсюда следует, что деформируемые системы и их элементы имеют бесконечное число степеней свободы. Но поскольку в кинематическом анализе не ставится задача определения реальных перемещений сооружений, то применяется гипотеза отвердения –предположение о недеформируемости материала всех элементов системы – как дисков, так и связей.

Точка, которую можно рассматривать как диск бесконечно малых размеров, на плоскости имеет две степени свободы – координаты x_A и y_A (рис. 1.28).

Несвязанный диск D в плоскости обладает тремя степенями свободы – это координаты точки x_A, y_A и угол наклона некоторой прямой α (рис. 1.29).

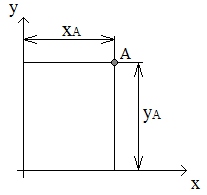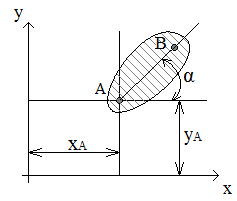Рис. 1.28. Степени свободы точки	Рис. 1.29. Степени свободы несвязанного диска в плоскости

---

Роль степеней свободы также могут играть не сами вышеуказанные координаты, а их приращения по отношению к некоторому исходному значению, т. е. линейные и угловые перемещения дисков.

Изменяемость системы – это свойство системы изменять свою геометрическую форму без деформации материала за счет конечных перемещений её элементов как твердых тел [1].

Степенью изменяемости системы V называется число независимых геометрических параметров, определяющих положение системы по отношению к одному её диску, принимаемому за неподвижный.

Поскольку неподвижный диск по отношению к земле обладает тремя степенями свободы, то между степенью свободы и степенью изменяемости имеется простая зависимость
V = W – 3. (1.3)
Степень свободы можно рассматривать как степень изменяемости РС, если в неё будет включена земля в качестве дополнительного диска.

В свою очередь степень изменяемости РС можно рассматривать как степень свободы её по отношению к одному диску, принимаемому условно за землю.

2. КИНЕМАТИЧЕСКИЙ АНАЛИЗ

РАСЧЕТНЫХ СХЕМ СООРУЖЕНИЙ

2.1. Основные положения

Инженерные сооружения, состоящие из отдельных элементов в виде твердых тел, как правило, несут различного вида нагрузки и, следовательно, являются геометрически неизменяемыми. Поэтому инженеру важно знать, как правильно соединять элементы сооружения, чтобы получить РСгеометрически неизменяемую, и как судить о геометрической неизменяемости РС, если она задана. После выбора РС для реального инженерного сооружения необходимо выполнить кинематический анализ РС.

Кинематический анализ РС – это исследование РС сооружения, выполняемое до начала расчета сооружения на прочность, жесткость и
устойчивость, для определения кинематического признака РС(геометрической неизменяемости, мгновенной изменяемости или геометрической изменяемости), а в случае геометрической неизменяемости РС– также для выявления её статической определимости или неопределимости [3].

---

В ходе кинематического анализа РС сооружения даются ответы на два главных вопроса [3].

1. Достаточно ли суммарное число внешних и внутренних связей в РС для того, чтобы при правильном их размещении обеспечить её геометрическую неизменяемость?

2. Правильно ли расставлены связи?

В связи с этим кинематический анализ РС сооружений проводится в два этапа.

А. На первом этапе аналитическим методом определяется степень свободы W или степень изменяемости V системы, т. е. устанавливается соотношение между суммарным числом степеней свободы дисков РС до наложения на них внешних и внутренних связей и суммарным числом внешних и внутренних связей РС,в пересчете на связи 1-го типа.

Указанный пересчет объясняется тем, что именно связь 1-го типа способна устранять, при правильном её использовании, одно возможное взаимное перемещение (линейное или угловое) соединяемых дисков, т. е. одну степень свободы.

Следует обратить внимание на то, что аналитический метод не дает ответа на вопрос – правильно ли расставлены связи? – метод оценивает их количество.

Первый этап завершается предварительным выводом о кинематической природе заданной РСсооружения.

Б. На втором этапе кинематического анализа РС проводится структурный анализ РС сооружения,т. е. исследуется структура расчетной схемы, заключающийся в проверке правильности расположения связей, выявлении возможных дефектов соединения дисков и завершающийся окончательным определением кинематического качества (природы) РС(её геометрической неизменяемости, изменяемости или мгновенной изменяемости).

---

2.2. Аналитический метод кинематического анализа

Суммарное число степеней свободы несвязанных дисков определяется из того, что каждый жесткий плоский диск обладает тремя степенями свободы. Наложение внешних и внутренних связей (в пересчете на связи
1-го типа) сокращает суммарное число степеней свободы несвязанных дисков [1]:

а) простая припайка (жесткий узел) – на три единицы (так как простая припайка эквивалентна трем связям 1-го типа);

б) простой шарнир – на две единицы (так как эквивалентен двум связям 1-го типа);

в) линейная связь – на единицу.

Обозначив через D число дисков РС(без учета диска «земля»);
С – число внутренних связей 1-го типа; С_оп – число внешних (опорных) связей 1-го типа; Ш – число простых шарниров (связей 2-го типа);
П – число простых припаек (связей 3-го типа), получим универсальную формулу определения числа степеней свободы РС,связанной с землей:
W = 3D – 3П – 2Ш – С – С_оп. (2.1)
Если в заданной системе нет замкнутых контуров без шарниров
(рис. 2.1, б), то припайки можно не учитывать при разделении РСна диски, тогда получим выражение
W = 3D – 2Ш – С – С_оп. (2.2)
Если считать внутренние связи 1-го типа за диски и не учитывать припайки при разделении РС,то можно получить выражение, более удобное для определения числа степеней свободы РС,
W = 3D – 2Ш – С_оп. (2.3)
Степень свободы РС, не имеющих опорных стержней (внешних связей 1-го типа), складывается из двух частей: степени изменяемости внутренней структуры РС и степени подвижности её относительно основания, которая равна трём.

Число степеней изменяемости V расчетной схемы, несвязанной с землей, определим по формулам:

V = W – 3 = 3D – 3П – 2Ш – С – 3;

V = W – 3 = 3D – 2Ш – С – 3;

V = W – 3 = 3D – 2Ш – 3.

Для шарнирно-стержневых систем (ферм), т. е. РС,состоящих из стержней, соединенных между собой по концам шарнирами (причем каждый стержень прикрепляется к соседним только двумя шарнирами), степень свободы может быть определена по формуле
W = 2У – С – С_оп, (2.4)
где У – число узлов в шарнирно-стержневой РС; С – число внутренних стержней фермы (число внутренних связей 1-го типа);

---

С_оп – число опорных стержней (число внешних связей 1-го типа).

Формула (2.4) получена исходя из того, что каждый узел как точка имеет на плоскости две степени свободы, а каждый стержень, соединяющий два узла, или опорный, эквивалентны связи 1-го типа, так как налагает на координаты этих точек единственное условие – постоянство расстояния.

Степень изменяемости РС,не имеющей опорных стержней V, определим по формуле

V = 2У – С – 3.

• 
  Узлом называется точка, в которой пересекается два или более стержней фермы.
  

При определении степени свободы или степени изменяемости РС на
1-м этапе кинематического анализа аналитическим методом возможны следующие три качественно различных результата [2]:

1) W > 0 или V > 0 – стержневая система структурно геометрически изменяемая, так как не имеет достаточного количества связей. Такая система называется механизмом;

2) W = 0 или V = 0 – стержневая система обладает необходимым минимумом связей, чтобы быть геометрически неизменяемой;

3) W < 0 или V < 0 – стержневая система имеет лишние связи.

Аналитические условия W ≤ 0, V ≤ 0 являются необходимыми, но недостаточными для суждения о геометрической неизменяемости сооружения.

Недостаточность условий геометрической неизменяемости проявляется в том, что оно имеет сугубо количественный характер и не может учесть возможных дефектов в размещении связей. Следовательно, выполнение необходимого условия геометрической неизменяемости не гарантирует того, что СС в действительности будет геометрически неизменяемой.

Вычисление характеристик W или V и проверка выполнения необходимого условия геометрической неизменяемости составляют содержание 1-го этапа кинематического анализа.
Порядок действий при определении степени свободы (изменяемости) расчетных схем аналитическим методом

1. 
   Проводим анализ геометрической структуры РС и определяем формулу, по которой проще вычислять степень свободы (изменяемости).
   

1.1. Если заданная РС имеет замкнутые контуры без шарниров
(рис. 2.1, а), то степень свободы (изменяемости) определяем по универсальным формулам:

W = 3D – 3П – 2Ш – С – С_оп;

V = 3D – 3

---