Файл: Реферат Расчетнопояснительная записка к курсовому проекту "Проектирование и исследование механизмов двигателя и передачи мотосаней".doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 60
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3) На каждом колесе строят профили трех зубьев, причем точка контакта К должна располагаться на активной линии зацепления. Профиль шестерни получается соответствующим поворотом зубьев полученных в станочном зацеплении. Эвольвентная часть профиля колеса строится, как траектория точки прямой при перекатывании ее по основной окружности колеса без скольжения, и переносится в точку контакта зубьев К на линию зацепления. Переходная часть профиля зуба строится приближенно.
4) На чертеже указываются диаметры начальных, делительных, основных окружностей, окружности вершин и впадин, шаг и толщина зубьев по делительным окружностям, высота зуба, межосевое расстояние, воспринимаемое смещение, угол зацепления, радиальный зазор, положения профилей в точках начала и конца зацепления, углы торцевого перекрытия (
3.6. Проектирование планетарного редуктора с цилиндрическими колесами.
При кинематическом синтезе многосателлитной планетарной передачи заданной схемы решаются задачи подбора таких чисел зубьев ее колес, которые будут удовлетворять условиям:
Выполнение заданного передаточного отношения;
-
Выполнение заданного передаточного отношения; -
Отсутствия заклинивания передачи, среза и подреза профилей зубьев колес; -
Соосность входного и выходного валов; -
Соседства; -
Сборки.
Первые три условия являются общими требованиями синтеза любой планетарной передачи. Остальные – это условия, диктуемые особенностями кинематических схем планетарных механизмов. Для двухрядного планетарного механизма с одним внешним и одним внутренним зацеплением воспользуемся методом сомножителей для подбора чисел зубьев колес.
Планетарная коробка передач состоит из двухрядного планетарного редуктора смешанного зацепления с тремя сателлитами. При проектировании редуктора используются следующие данные:
Передаточное отношение,
Число сателлитов, k = 3.
Задача определения числа зубьев сводится к составлению исходных уравнений, отражающих указанные условия и требования для каждой конкретной схемы и совместному их решению. Одним из наиболее распространённых методов определения Z является метод сомножителей, при котором Z определяется по передаточному отношению, условию соосности, условию отсутствию подреза и заклинивания, а проверяется по условию сборки, соседства и конструктивным ограничениям.
Из уравнения передаточного отношения
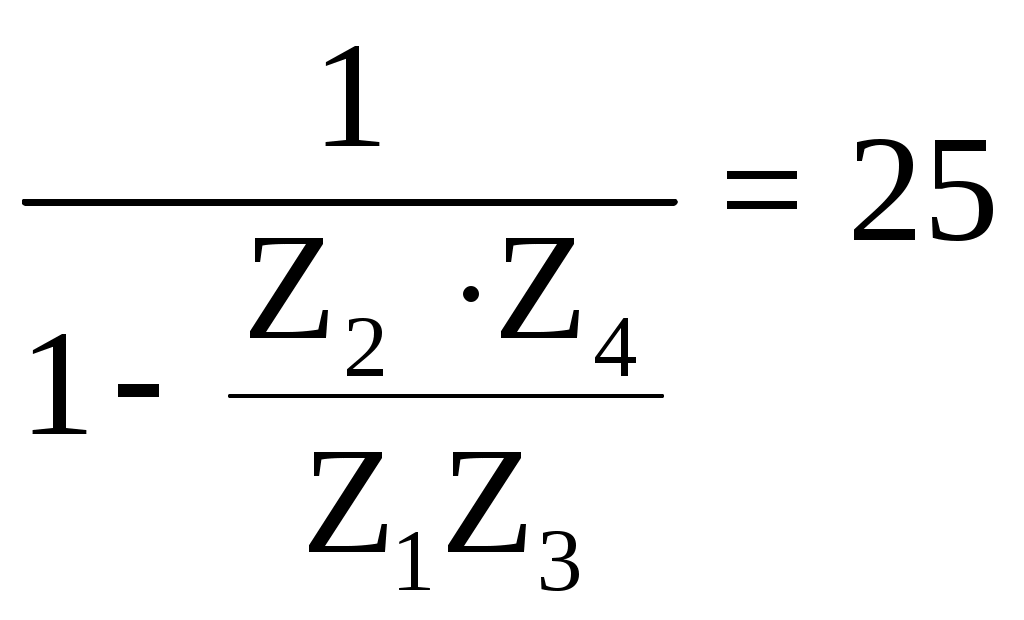 находим
находим Из условия соосности
Чтобы выполнялось это тождество, необходимо ввести множитель пропорциональности q – любое положительное число, обеспечивающее условия правильного зацепления. Тогда
Выберем
.
Проектируемый редуктор должен удовлетворять следующим требованиям:
1) Он должен обеспечивать необходимое передаточное отношение. Для этого записывают выражение, связывающее между собой количество зубьев колес планетарного редуктора (Z1,Z2,Z3,Z4) и заданное передаточное отношение. В нашем случае выражение имеет вид:
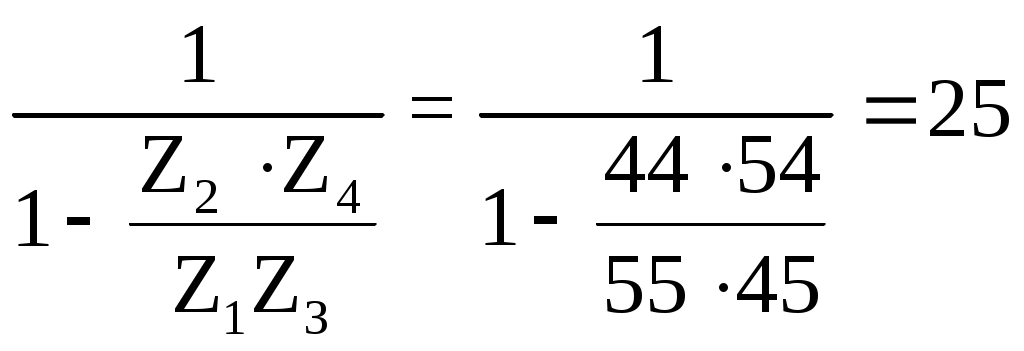
2) Должно соблюдаться условие соосности, т.е. оси центральных колес при назначенных Z должны совпадать с осью водила. В нашем случае выражение условия соосности имеет вид:
Z1+Z2=Z3+Z4 или 55+44=45+54 – условие соосности выполняется.
3) Должно выполняться условие соседства (совместности), т.е. должна быть возможность размещения нескольких сателлитов по общей окружности в одной плоскости без соприкосновения друг с другом. Выражение условия соседства имеет вид:
0,866>0.478 – условие совместности выполняется.
4) Должно соблюдаться условие сборки, т.е. должна обеспечиваться возможность одновременного зацепления всех сателлитов с центральными колесами при равных углах между сателлитами:
5) Должно соблюдаться условие отсутствия подрезания, т.е. при колесах нарезанных стандартным инструментом без смещения (при
Все условия выполняются.
Рассчитаны радиусы колес в планетарном редукторе:
,
3.7 Графическая проверка.
Была вычерчена схема спроектированного планетарного механизма в масштабе l=1500 мм/м.
Выберем на водиле точку F , так чтобы L01F=L02A . Зададимся произвольным отрезком FF΄, который изображает линейную скорость точки F водила. Так как водило вращается вокруг оси O1 , то закон распределения линейных скоростей по водилу изображен линией Н, проходящей через точки О и F΄. В точке В водило имеет линейную скорость, изображенную отрезком ВВ΄.
Второе колесо имеет в точке В точно такую же скорость, то есть закон распределения линейных скоростей по второму колесу изображен линией 2 , проходящей через точки С и В΄.
В точке А второе колесо имеет скорость , которая изображена отрезком АА΄,
а так как точка А принадлежит и первому колесу , то есть первое и второе колеса имеют одинаковые скорости в точке А и первое колесо вращается вокруг оси О2 ,поэтому закон распределения линейных скоростей по первому колесу будет представлен линией 1 , проходящей через точки О и А΄.
Найдём передаточное отношение по графику:
4. Проектирование кулачкового механизма.
4.1 Исходные данные
Ведущее звено – плоский вращающийся кулачок, ведомое – совершающий возвратно-поступательное движение роликовый толкатель. В качестве обобщенной координаты принимается угол поворота кулачка. Закон изменения ускорения толкателя приведен в техническом задании в виде графика. Кроме того, определены следующие исходные данные:
-график изменения ускорения толкателя (рис.3);
-угол рабочего профиля кулачка - раб = 120˚;
-максимальный ход толкателя h=0,008 м;
-кулачок с поступательным толкателем;
-допустимый угол давления в кулачковом механизме - αдоп =28˚.
4.2 Определение частоты вращения кулачкового вала
При номинальной нагрузке вращение распределительному валу 7 передаётся от коленчатого вала 1 парой зубчатых колёс 10 и 11 (рис.2), передаточное отношение которой

