Файл: Курсоваяработ а по дисциплине Математический анализ Поверхностные интегралы и их приложения Выполнил(а) студент (ка).docx

( В равенствах (3) – (5) величины cosα, cosβ, cosγ есть направляющие косинусы вектора нормали к поверхности ).

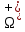Складывая соотношения (3) – (5) получаем формулу Стокса:



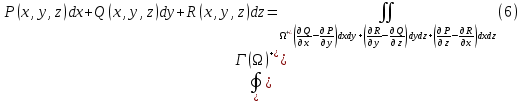
Формулу Стокса можно записать и через поверхностный интеграл I-го рода:



Замечание 1. Вектор называется ротором, или вихрем векторной функции 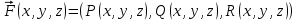.Компоненты ротора удобно выразить с помощью определителя: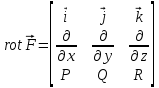



С использованием понятия ротора формула Стокса записывается короче:



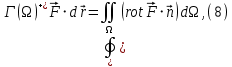
и выражает циркуляцию вектора через поверхностный интеграл от его ротора.

(Основано на Калинин В.В., Петрова И.В. К 18 Математика в нефтегазовом образовании. Теория и задачи: Учеб. пособие. − М.: РГУ нефти и газа им. И.М. Губкина, 2005. Вып. 3. Часть 2: Кратные, криволинейные и поверхностные интегралы – 161- 165с)

---

1.5 Формула Остроградского

Формула Остроградского связывает тройной интеграл по пространственной области с поверхностным интегралом по границе области.

Рассмотрим тело (V), ограниченное гладкими поверхностями



и цилиндрической поверхностью( 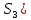, образующие которой параллельны оси z. Направляющей здесь служит кусочно-гладкая замкнутая кривая (К) (с нулевой площадью) на плоскости xy, ограничивающая область (D) – проекцию тела (V) на эту плоскость.

Допустим, что в области (V) определена некоторая функция R (x, y, z), непрерывная вместе со своей производной 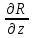во всей области (V), включаяя ее границу. Тогда имеет место формула

,

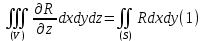причем (S) есть поверхность, ограничивающая тело, и интеграл справа распространен на внешнюю ее сторону.

Действительно,



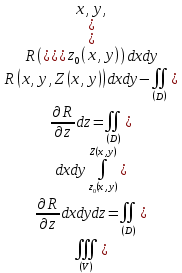
Если ввести в рассмотрение поверхностные интегралы, то, в силу формул



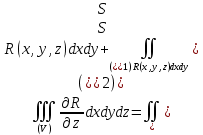
причем первый из интегралов справа распространен на верхнюю сторону поверхности 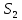, а второй – на нижнюю сторону поверхности 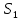. Равенство не нарушится, если мы прибавим к правой его части интеграл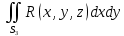



распространенный на внешнюю сторону поверхности , так как этот интеграл равен нулю. Объединяя все три поверхностных интеграла в один, мы и придем к формуле Остроградского.

Легко понять, что формула (1) верна для более широкого класса тел, которые могут быть разложены на части изученного типа. Можно доказать также, что формула (1) справедлива вообще для тел, ограниченных произвольными кусочно-гладкими поверхностями.

Аналогично формуле (1) имеют место и формулы:

---

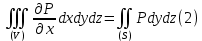
если функции P и Q непрерывны в области (V) вместе со своими производными и .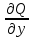

Сложив все три формулы (1), (2), (3), мы и придем к общей формуле Остроградского:



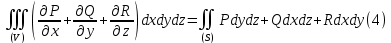
Она выражает общего вида поверхностный интеграл второго типа, распространенный на внешнюю сторону замкнутой поверхности, через тройной интеграл, взятый по телу, ограниченному этой поверхностью.

Если привлечь к рассмотрению поверхностные интегралы первого типа, то получим другой, весьма употребительный и легко запоминаемый вид формулы Остроградского:



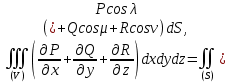
где 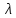, , 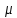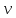углы, составленные внешней нормалью к поверхности (S) с координатными осями.
(Основано на Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Т.2. Санкт – Петербург: Лань, 1997 – 340 – 342с)

1.6 Некоторые приложения формулы Остроградского

1) Представление объема тела поверхностными интегралами. Можно различными способами подобрать функции P, Q, R так, чтобы подынтегральное выражение в тройном интеграле оказалось равным единице, так что этот интеграл сведется к объему V тела (V). Таким образом, объем V представится в виде поверхностного интеграла, распространенного на ограничивающую тело (V) поверхность (S).

Так, полагая в (4) поочередно

,

придем к формулам:



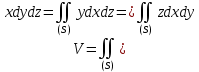
причем все интегралы взяты по внешней стороне поверхности (S). Удобной является более симметричная формула, отвечающая



она имеет вид



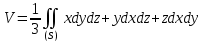
или – если перейти к интегралу первого типа

---

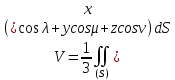
(здесь 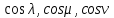означают направляющие косинусы внешней нормали 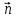к поверхности)

Можно представить эту формулу еще иначе: если рассмотреть вектор , соединяющий начало с переменной точкой поверхности, с проекциями x, y ,z на оси координат, то выражение в скобках может быть переписано в виде



и, окончательно,



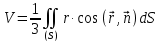
2) Равновесие жесткой замкнутой поверхности. Докажем, что жесткая замкнутая поверхность, подвергнутая всестороннему давлению, остается в равновесии.

С этой целью установим, что равны нулю главный вектор и главный момент (относительно какой-либо точки) всей системы приложенных е поверхности сил.

Выделим элемент dS поверхности. Если через p= const обозначить давление, т.е. силу, действующая на dS по нормали к этому элементу, будет иметь проекции на оси



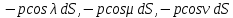
(знак минус поставлен потому, что давление направлено внутрь поверхности, а 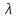, углы внешней нормали с координатными осями).

Проекции 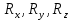главного вектора получаются из проекции элементарных сил суммированием их: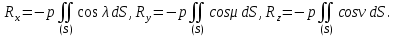



Но все эти интегралы равны нулю, что видно из формулы Остроградского, если положить в ней



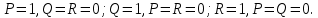
Итак, главный вектор равен нулю.

Для определения главного момента системы элементарных сил, скажем, относительно начала координат, просуммируем проекции на оси моментов этих элементарных сил:



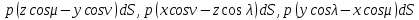
Таким образом, проекции главного момента давлений относительно начала будут:

---

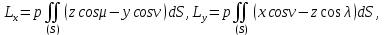
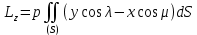
Если в формуле Остроградского взять P=0, Q=pz, R= -py, то получим, что . Так же легко установить, что и 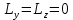. Главный момент давлений (относительно начала) равен нулю. Этим и завершается доказательство.

3) Закон Архимеда. Известно, что давление жидкости на погруженную в нее площадку направлено по нормали к площадке и равно весу столба жидкости, основанием которого служит эта площадка, а высотой – глубина погружения площадки. Допустим теперь, что в жидкость погружено твердое тело V; на каждый элемент dS его поверхности S по указанному закону давит жидкость. Требуется определить равнодействующую элементарных давлений и ее точку приложения.

Для решения этой задачи выберем координатную систему, совместив плоскость xy со свободной поверхностью жидкости, а ось z направив вертикально вниз.

Пусть удельный вес жидкости равен p, а глубина погружения элемента dS есть z; тогда испытываемое этим элементом давление будет



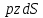
а проекции его на оси



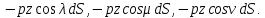
В таком случае для проекций главного вектора на оси имеем:



С помощью формулы Остроградского, как и в предыдущей задаче, легко получить



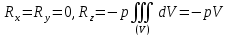
Таким образом, главный вектор давлений направлен вертикально вверх и равен весу вытесненной телом жидкости.

Рассмотрим теперь моменты элементарных сил относительно центра тяжести 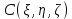тела ( здесь и дальше имеется в виду центр тяжести геометрического тела, при равномерном распределении масс; он может не совпадать с центром тяжести физического тела). Составляющие элементарных моментов по осям будут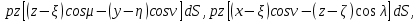





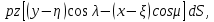
а для составляющих главного момента (относительно точки C) получим:

---