Файл: Курсоваяработ а по дисциплине Математический анализ Поверхностные интегралы и их приложения Выполнил(а) студент (ка).docx

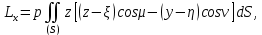
Применяя к интегралу формулу Остроградского, найдем



ибо интеграл 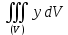есть статический момент тела относительно плоскости xz и равен . Аналогично устанавливается, что 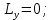непосредственно получается, наконец, что и .

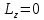Итак, главный момент давлений относительно центра тяжести тела равен нулю. Сопоставляя это утверждение с ранее доказанным предположением о главном векторе, приходим к такому заключению: на тело, погруженное в жидкость, со стороны последней действует сила, равная весу жидкости, вытесненной телом; эта сила приложена к центру тяжести (геометрического) тела и направлена вертикально вверх.
(Основано на Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Т.2. Санкт – Петербург: Лань, 1997 – 342 – 345с)

---

2.Решение задач, связанных с поверхностными интегралами

• 
  Пример 1.
  

Вычислить циркуляцию вектора 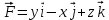вдоль линии γ пересечения сферы и конуса 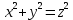, z > 0.
Для точек, лежащих на кривой γ, справедливы равенства: .

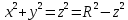Тогда координаты точек, лежащих на кривой γ, удовлетворяют соотношениям: _z² = _R² /2, _x² + _y² = _R² /2, т.е. кривая γ – это окружность радиуса , лежащая в плоскости .

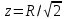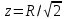Применим формулу Стокса. В качестве поверхности Ω возьмем круг радиуса , лежащий в плоскости . Кривая γ является границей этого круга, т.е. 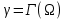. Положительным направлением обхода контура будем считать направление против часовой стрелки, если смотреть со стороны положительной части оси OZ (рис. 16). Вектор 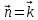является вектором нормали к Ω, соответствующим выбранному положительному направлению обхода контура.

На поверхности Ω имеем: dΩ = dxdy. Ротор вектора 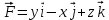равен: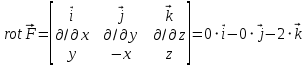



Проекция поверхности Ω на плоскость OXY представляет собой круг D радиуса . По формуле получаем:



Рисунок 6. К примеру 1

• 
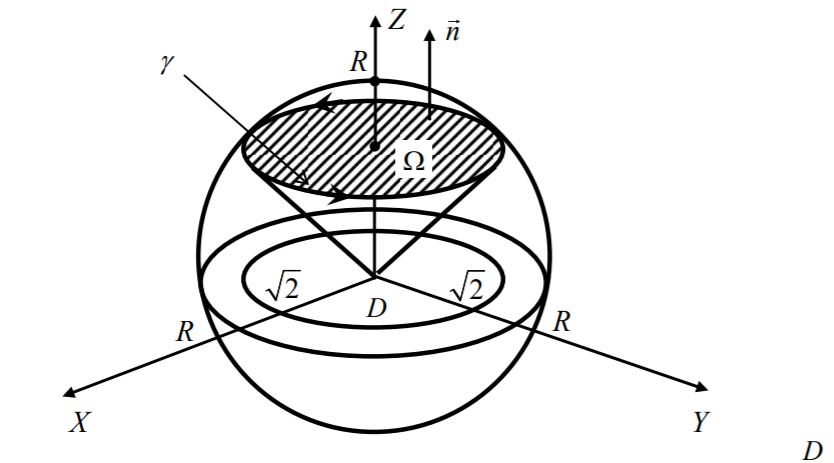
  Пример 2
  

Вычислить циркуляцию вектор-функции

---

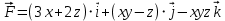
вдоль линии γ пересечения параболоида 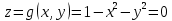(рис. 17) с координатными плоскостями (x ≥ 0, y ≥ 0, z ≥ 0).

Воспользуемся формулой Стокса. В качестве поверхности Ω с границей γ примем часть параболоида, лежащую в первом октанте, т.е. при x ≥ 0, y ≥ 0, z ≥ 0. Таким образом, γ = Г(Ω). Положительным направлением обхода контура будем считать движение против часовой стрелки, если смотреть со стороны внешней нормали к параболоиду:

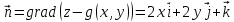
На поверхности Ω имеем:



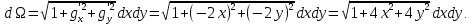
Найдем теперь ротор вектора :



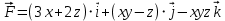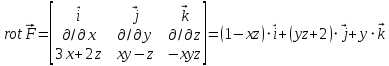
Проекция поверхности Ω на плоскость OXY представляет собой четверть круга D: + =1, x ≥ 0, y ≥ 0.

На поверхности Ω в цилиндрических координатах выполнено равенство 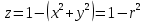. Тогда по формуле Стокса получим:



(Последний интеграл может быть вычислен с помощью замены переменных ).

• 
  
  
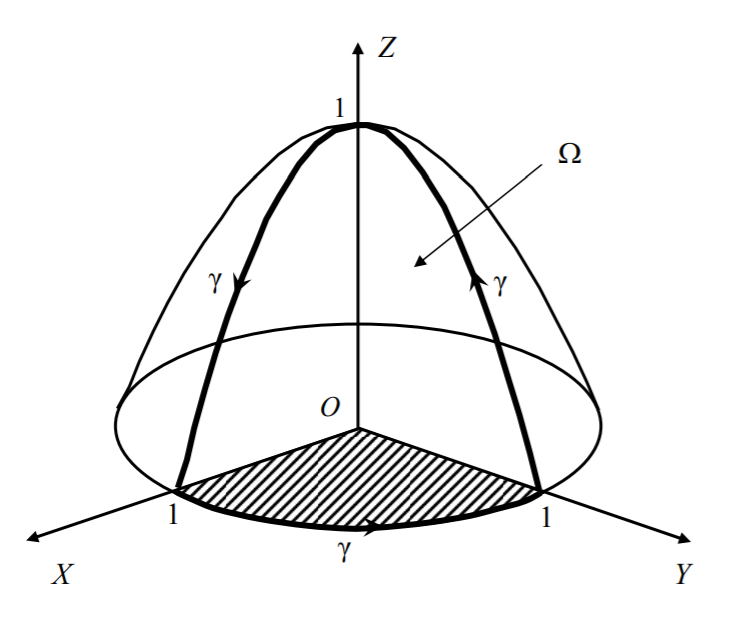
  Рисунок 7. К примеру 2
  Пример 3.
  

Вычислить поток вектора 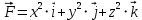через внешнюю поверхность куба 0 ≤ x ≤ a, 0 ≤ y ≤ a, 0 ≤ z ≤ a.



Рисунок 8. К примеру 3
Пусть Ω – поверхность куба V, а – внешняя нормаль к его поверхности (рис.18). По формуле Остроградского получаем: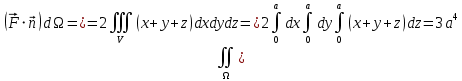

• 
  Пример 4.
  

---

Пусть по поверхности Ω сферы распределена масса с плотностью . Найти массу сферы Ω.

Разобьем поверхность Ω на части Ωk столь мелкие, что в пределах каждой из них плотность можно считать постоянной. Выберем в каждой части Ωk по произвольной точке Mk. Тогда масса поверхности приближенно равна значению



и представляет собой интегральную сумму поверхностного интеграла I-го рода от функции ρ(M) по поверхности Ω. Чем меньше части разбиения, тем точнее получается формула. В пределе для массы поверхности получаем:



Введем сферические координаты:



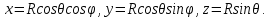
Тогда







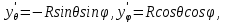
Найдем гауссовские коэффициенты поверхности Ω:







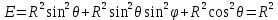
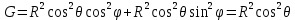
Тогда по формуле получаем искомую массу поверхности сферы:

• 
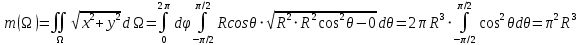
  Пример 5.
  

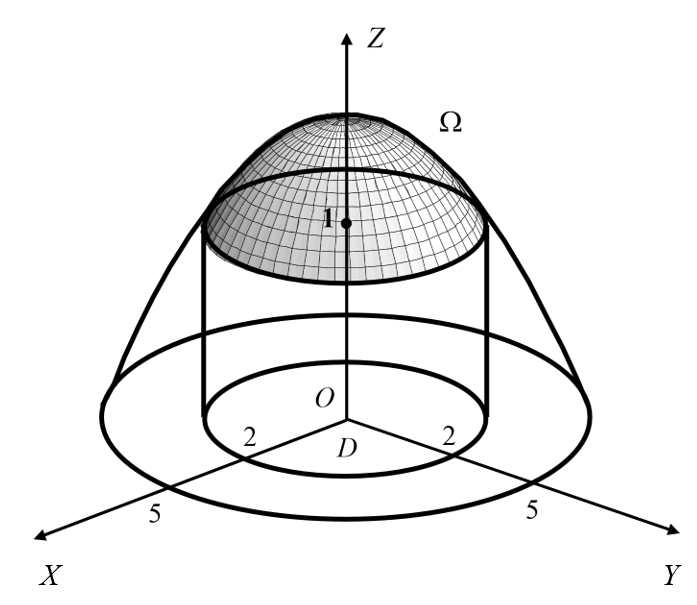
Рисунок 9. К примеру 5
Вычислить площадь части параболоида , отсекаемой плоскостью z = 1 (рис. 19).

В этом примере 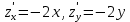и .

Тогда получаем: , где D – круг в плоскости OXY радиуса 2 с центром в начале координат. Переходя к полярным координатам, получаем:

Заключение

Интеграл – одно из основных понятий математического анализа возникшее в связи с потребностью, с одной стороны, отыскивать функции по их производным, например, находить длину пути, пройденного движущейся точкой, по её скорости. С другой стороны, измерять площади, объемы, работу сил за определенный промежуток времени и т.п. В

---

заключение можно сказать, что тема поверхностных интегралов важна для изучения в учебных заведениях, так как имеет отражение не только в геометрии и алгебре, а также и в физике. Понятие поверхностного интеграла используют такие задачи как задача нахождения массы поверхности, имеющей поверхностную плотность, применяется при нахождении циркуляции векторного поля, нахождение объема тела, нахождение потока векторного поля по замкнутой поверхности и т.д.

Были рассмотрены основные теоремы, применяемые при решении задач, формулы, связывающие поверхностные интегралы с криволинейными интегралами по контуру границы поверхности и тройной интеграл по пространственной области с поверхностным интегралом по границе этой области. Поверхностный интеграл является таким же обобщением двойного интеграла, каким криволинейный интеграл является по отношению к определенному интегралу.

Собрав и систематизировав материал по поверхностным интегралам, я проделал большую работу в сфере анализа, интегрального исчисления, физических приложений. Данный материал можно демонстрировать в университетах, как на математических дисциплинах – алгебра, математический анализ, геометрия; так и на физических дисциплинах – теоретическая механика и электростатика.

Список использованной литературы

1.Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Т.2. Санкт – Петербург: Лань, 1997.[Электронный ресурс]- https://vk.com/doc44301783_509485129?hash=4396565930922fa48c&dl=1b99edf9ef9e0a845d

2. Калинин В.В., Петрова И.В. К 18 Математика в нефтегазовом образовании. Теория и задачи: Учеб. пособие. − М.: РГУ нефти и газа им. И.М. Губкина, 2005. Вып. 3. Часть 2: Кратные, криволинейные и поверхностные интегралы. [Электронный ресурс]- http://kvm.gubkin.ru/vip3p2/beg2.pdf

3.Феоктистов, Ю. А. Ф-42 Кратные, криволинейные и поверхностные интегралы / Ю. А. Феоктистов. – Белгород: Изд-во БГТУ, 2019. [Электронный ресурс]- https://www.elibrary.ru/download/elibrary_39278777_44418465.pdf

4.Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1. М.: Наука, 1995. [Электронный ресурс]- https://studfile.net/preview/9245228/

5.Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.2. М.: Наука, 1995 1. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Т.

---