Файл: Курсоваяработ а по дисциплине Математический анализ Поверхностные интегралы и их приложения Выполнил(а) студент (ка).docx
Добавлен: 10.04.2024
Просмотров: 125
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1.1Определение поверхностного интеграла первого типа
1.2 Физические приложения поверхностных интегралов первого типа
1.3 Поверхностный интеграл II-го рода
1.3.1 Выражение поверхностного интеграла II-го рода через двойной интеграл.
1.6 Некоторые приложения формулы Остроградского
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«МУРМАНСКИЙ АРКТИЧЕСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
(ФГБОУ ВО «МаГУ»)
Факультет математичеких и естественных наук
Кафедра Математики, физики и информационных технологий
К У Р С О В А Я Р А Б О Т А
по дисциплине «Математический анализ»
Поверхностные интегралы и их приложения
Выполнил(а) студент (ка):
Осокин А.Д.
3БПО-МФ, ФМиЕН
Научный руководитель:
_____________________
к.п.н., доцент
Оглавление
Введение 3
1.1Определение поверхностного интеграла первого типа 4
1.2 Физические приложения поверхностных интегралов первого типа 9
1.3 Поверхностный интеграл II-го рода 14
1.3.1 Выражение поверхностного интеграла II-го рода через двойной интеграл. 18
1.4 Формула Стокса. 20
1.5 Формула Остроградского 24
1.6 Некоторые приложения формулы Остроградского 26
2.Решение задач, связанных с поверхностными интегралами 31
Заключение 37
Список использованной литературы 38
Введение
Понятие интеграла возникло ещё несколько веков назад в связи с возрастающими потребностями человечества. Прикладная направленность интегрального исчисления выражается в различного рода, задачах, среди которых задача нахождения длины пути, задача нахождения площадей, объемов и т.д. Особый интерес для исследования представляет поверхностный интеграл. Понятие поверхностного интеграла используют такие задачи как задача нахождения массы поверхности, имеющей поверхностную плотность. Поверхностные интегралы существуют двух видов, это поверхностные интегралы первого и второго рода. С поверхностным интегралом второго рода связаны две формулы, находящие разнообразные применения, в том числе в физических приложениях. Это формулы Стокса и Остроградского-Гаусса. Формула Стокса применяется при нахождении циркуляции векторного поля. Формула Остроградского-Гаусса имеет множество применений, среди которых нахождение объема тела, нахождение потока векторного поля по замкнутой поверхности и т.д.
Целью данной работы является исследование поверхностного интеграла первого и второго рода, а также их практического применения.
Объектом данной работы является интегральное исчисление функции нескольких переменных.
Предметом данной работы является вычисление поверхностных интегралов первого и второго рода.
Задачи работы:
1.Систематизировать теоретический материал по данной теме.
2.Рассмотреть определение и свойства поверхностных интегралов первого и второго рода.
3.Выявить практическое применение данного материала в физике.
4.Рассмотреть некоторые примеры задач по применению поверхностных интегралов
5.На основе теоретического и практического материала сделать выводы
1.1Определение поверхностного интеграла первого типа
Теория поверхностных интегралов во многом аналогична теории криволинейных интегралов. Рассматриваются интегралы двух типов: поверхностные интегралы I-го и II-го рода, их определения аналогичны соответствующим определениям для криволинейных интегралов, для определения поверхностного интеграла II-го рода на поверхности необходимо задать ориентацию. Как и для криволинейных интегралов, существуют формулы, связывающие поверхностные интегралы I-го и II-го рода. Однако в отличие от кривой, которая определяется заданием одного параметра, для описания поверхности необходимо уже два параметра, поэтому вычисление поверхностных интегралов сводится к вычислению двойного интеграла по области на плоскости (а не определенного интеграла Римана, как для криволинейных интегралов).
Поверхностный интеграл I-го рода.
В трехмерном пространстве с декартовой системой координат ОXYZ рассмотрим кусочно-гладкую поверхность Ω, ограниченную кусочно-гладкой кривой
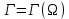 . В частном случае замкнутой поверхности (например, сферы) ее граница представляет собой пустое множество, а значит также является кусочно-гладкой.
. В частном случае замкнутой поверхности (например, сферы) ее граница представляет собой пустое множество, а значит также является кусочно-гладкой.Пусть на поверхности Ω задана функция f(M), где
 – точка на поверхности, а (х, у, z) – ее декартовы координаты. Пусть функция f(M) непрерывна на поверхности Ω, т.е. в ранее введенных обозначениях
– точка на поверхности, а (х, у, z) – ее декартовы координаты. Пусть функция f(M) непрерывна на поверхности Ω, т.е. в ранее введенных обозначениях 
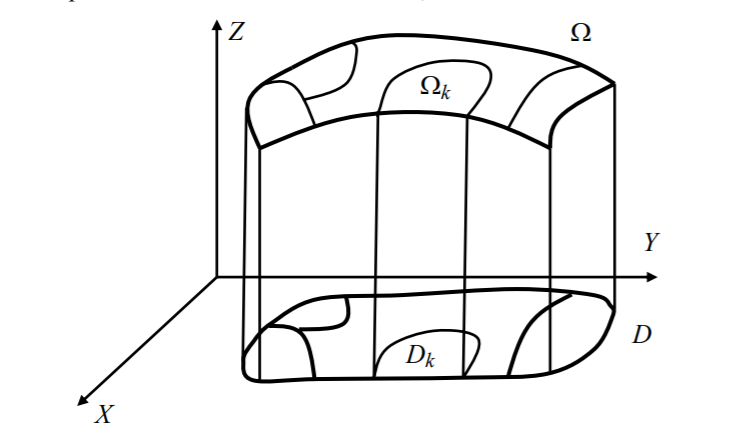
Зададим разбиение T поверхности Ω с помощью произвольно проведенных кусочно-гладких кривых на части
 (рис. 1). В каждой из этих частей Ωk выберем по произвольной точке
(рис. 1). В каждой из этих частей Ωk выберем по произвольной точке 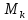 с координатами
с координатами 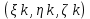 , и составим интегральную сумму:
, и составим интегральную сумму:


Рисунок 1. К определению поверхностного интеграла I рода
Где
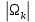 – площадь поверхности Ωk.
– площадь поверхности Ωk.Определение 1. Пусть P и N– произвольные точки части Ωk поверхности Ω. Соединим эти точки дугой γ гладкой кривой, целиком лежащей в Ωk. Обозначим через γ(P, N) длину этой дуги, а через ℓ(P, N) – длину самой короткой дуги, соединяющей точки P и N и целиком лежащей на поверхности Ωk:
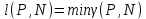 Диаметром части
Диаметром части  поверхности
поверхности 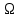 назовем величину γ
назовем величину γ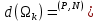 Диаметром dT разбиения T будем называть наибольший
Диаметром dT разбиения T будем называть наибольший 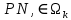 из диаметров частей:
из диаметров частей: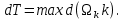
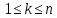
Определение 2. Поверхностным интегралом I-го рода от функции
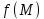 по поверхности
по поверхности 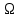 называется предел интегральной суммы (1) при бесконечном увеличении числа n частей разбиения
называется предел интегральной суммы (1) при бесконечном увеличении числа n частей разбиения 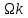 и бесконечном уменьшении диаметра
и бесконечном уменьшении диаметра  разбиения, если этот предел существует и не зависит ни от способа разбиения T, ни от выбора точек
разбиения, если этот предел существует и не зависит ни от способа разбиения T, ни от выбора точек
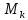 :
: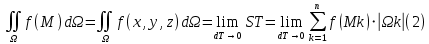
Для поверхностного интеграла используются и другие обозначения:
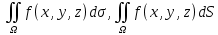
Сформулируем без доказательства теорему о существовании поверхностного интеграла I-го рода:
Теорема 1. Если Ω – непрерывная кусочно-гладкая поверхность, ограниченная кусочно-гладкой кривой Г(Ω), и функция f(M) непрерывна на ней, то поверхностный интеграл I-го рода (2) от функции f(M) существует и определен однозначно.
Обратимся теперь к вычислению поверхностного интеграла I-го рода.
Теорема 2. Пусть Ω – гладкая поверхность, заданная на ограниченной области D плоскости OXY уравнением:
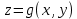 , где
, где  , и пусть функция f(M) непрерывна на этой поверхности. В этом случае поверхностный интеграл I-го рода от функции f(M) находится по формуле:
, и пусть функция f(M) непрерывна на этой поверхности. В этом случае поверхностный интеграл I-го рода от функции f(M) находится по формуле: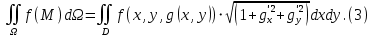

Рисунок 2. К доказательству теоремы 2
Доказательство теоремы 2. Спроектируем на плоскость
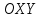 множество кривых, разбивающих поверхность Ω на части Ωk (рис.2). Получим в результате разбиение области D на части
множество кривых, разбивающих поверхность Ω на части Ωk (рис.2). Получим в результате разбиение области D на части  .
.
По формуле имеем выражение для площади поверхности Ωk:
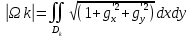
Это равенство можно преобразовать, применив теорему о среднем для двойного интеграла:
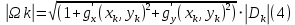
где
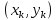 – некоторая точка части
– некоторая точка части , а
, а 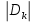 – площадь этой части.
– площадь этой части. Подставляя формулу (4) в выражение (1) для интегральной суммы, получим:
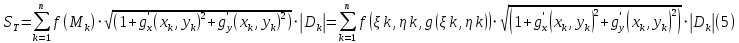
Отметим, что выражение (5) отличается от интегральной суммы
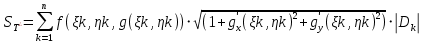
двойного интеграла
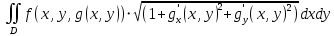
только значениями аргументов частных производных
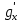 и
и 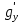 под знаком квадратного корня. В силу предположения о гладкости поверхности эти частные производные непрерывны на замыкании
под знаком квадратного корня. В силу предположения о гладкости поверхности эти частные производные непрерывны на замыкании 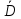 области D. Тогда и функция
области D. Тогда и функция 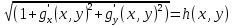 также непрерывна на
также непрерывна на 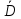
Функция, непрерывная на замкнутой (т.е. содержащей свою границу) ограниченной области является равномерно непрерывной на ней, т.е. для любого значения
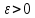 существует такое
существует такое 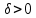 , что при диаметре
, что при диаметре  разбиения меньшим δ, разность
разбиения меньшим δ, разность 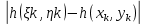 будет меньше ε .
будет меньше ε .Из непрерывности на поверхности Ω функции f(M) следует, что функция
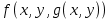 непрерывна, а следовательно, и ограничена на области
непрерывна, а следовательно, и ограничена на области 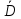 :
: 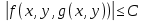
Тогда получаем, что при
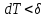 выполнено неравенство
выполнено неравенство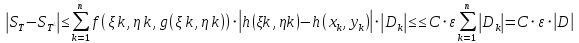
поэтому при
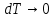 разность
разность 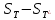 → 0, т.е. пределы интегральных сумм
→ 0, т.е. пределы интегральных сумм 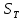 и
и 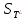 совпадают:
совпадают: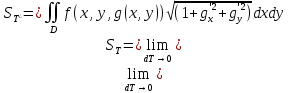
Отсюда и следует утверждение теоремы 2.
Замечание. Интегральная сумма (1) для функции