Файл: Курсовая работа 40 страниц.doc

3.5 ОДПФ для получения дискретного сигнала

Восстановим значения , применив ОДПФ к коэффициентам по формуле

, где , (3.9)
, что полностью совпадает с рассчитанным в пункте 3.2.

3.6 Восстановление аналогового сигнала по ДПФ

По найденным ранее коэффициентам ДПФ можно восстановить исходный сигнал с ограниченным спектром. Ряд Фурье для такого сигнала принимает вид конечной суммы гармонических сигналов:

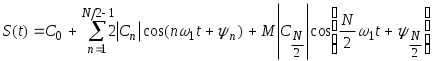(3.10)

В нашем случае формула (3.10) приобретает следующий вид:




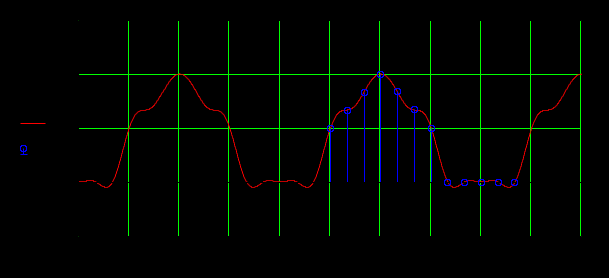
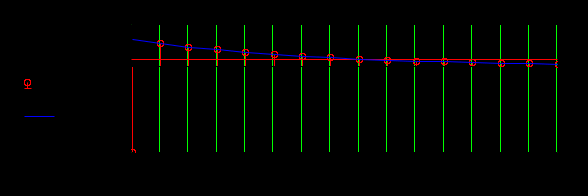
Рисунок 3.9 Аналоговый сигнал, восстановленный по коэффициентам ДПФ
Восстановленный сигнал по Фурье точно проходит через отсчеты выборки. Точность восстановления, как видно из рисунка 3.9, зависит от значения числа .

3.7 Восстановление аналогового сигнала по ряду Котельникова

Воспользуемся рядом Котельникова: 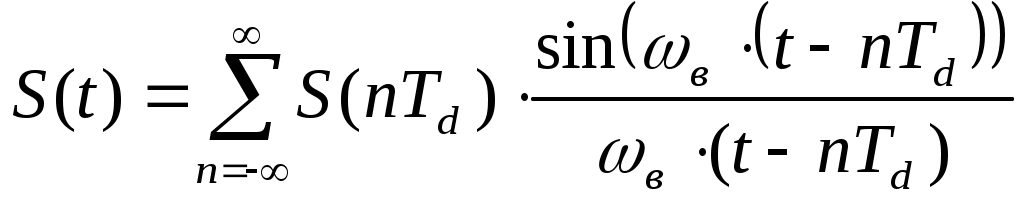(3.11)

Для нашего случая: , тогда (3.11) можно представить в следующем виде:

---

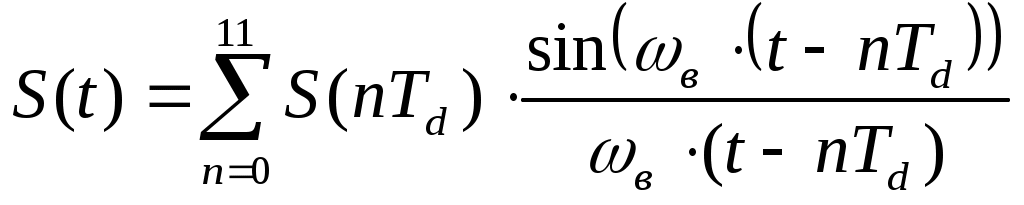
(3.12)

Вместе с восстановленным сигналом изобразим 2 функции Котельникова в точках {1} и {2}.





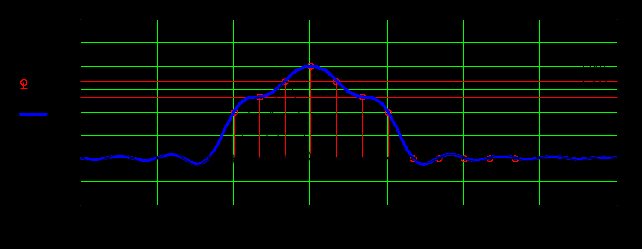
Рисунок 3.10 Аналоговый сигнал, восстановленный по ряду Котельникова
Как видно из рисунка 3.10 восстановленный сигнал точно проходит через отсчеты выборки. Это объясняется математическим свойством функции Котельникова. Значения исходного сигнала и периодического совпадают только в точках отсчета.

3.8 Расчёт спектральной плотности полученного дискретного сигнала, основанной на применении прямого Z – преобразования

Прямое z- преобразование последовательности определяется формулой:

(3.13)

Найдем z- преобразование элементарных составляющих сигнала, после этого просуммируем их. В нашем случае имеется 2 элементарных сигнала:

1. Функция Хевисайда : , (3.14)

2. Прямая: : , (3.15)

Сдвиг функции Хевисайда или прямой приводит к умножению Z – образа на оператор сдвига . Воспользовавшись выражениями (3.14) и (3.15) получим:
,

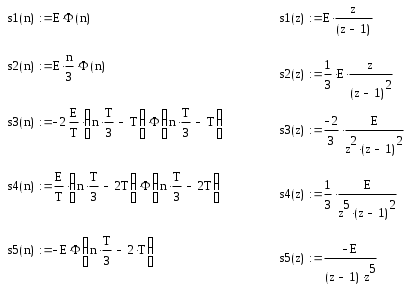где дискретизированная функция Хевисайда.

Тогда имеем или
(3.16)
Для того чтобы на основе Z – образа последовательности отсчётов было возможно получить спектральную плотность

---

, необходимо сделать замену вида:

.

(3.17)

По формуле (3.17) построим спектральную плотность:


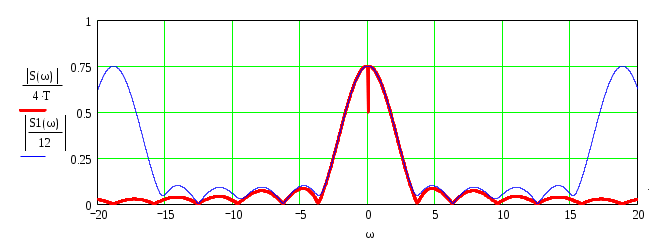
Рисунок 3.11 Спектральная плотность дискретизированного и аналогового сигнала

---

3.9 Выводы

По проделанной в этом пункте работе можно сделать следующие заключения:

• 
  Спектральная плотность нашего аналогового сигнала есть непериодическая функция частоты, достигающая своего максимума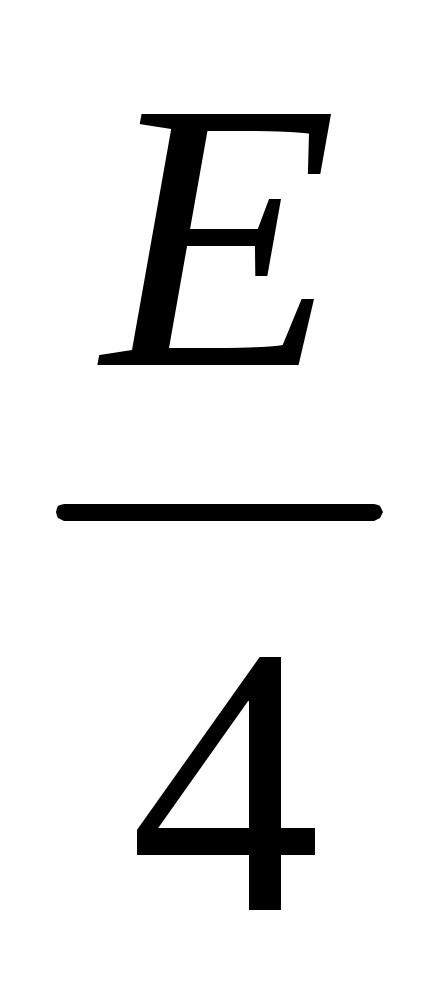 на нулевой частоте. Продискретизировав сигнал, мы получили периодическую спектральную функцию с периодом 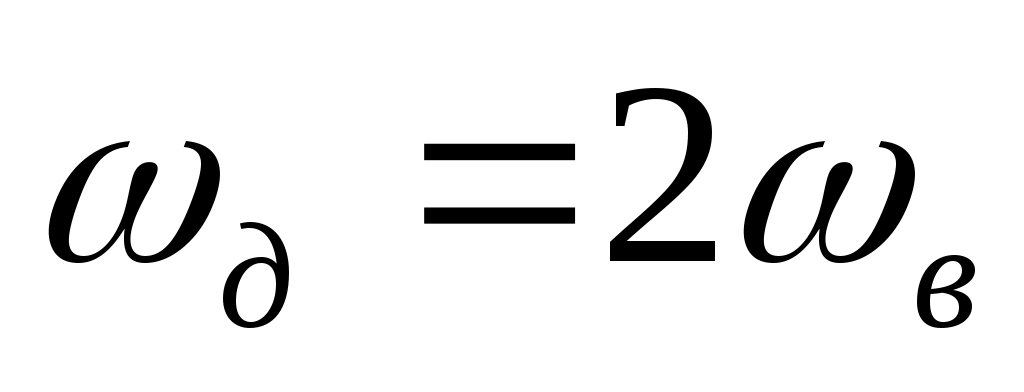(рис. 3.5). Не совпадение точек пересечения с осью произошло из-зи неправильного выбора 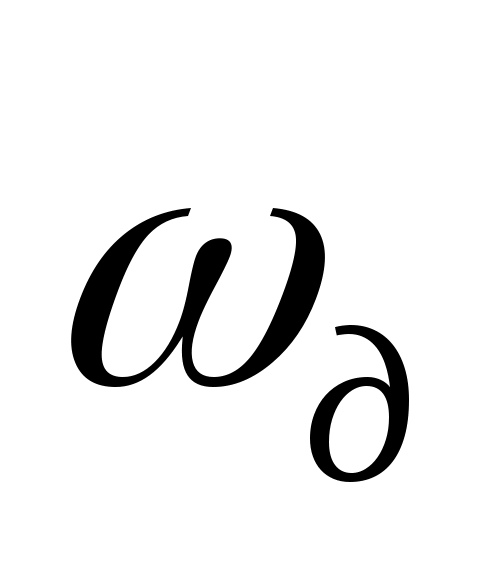, тем не менее, спектр 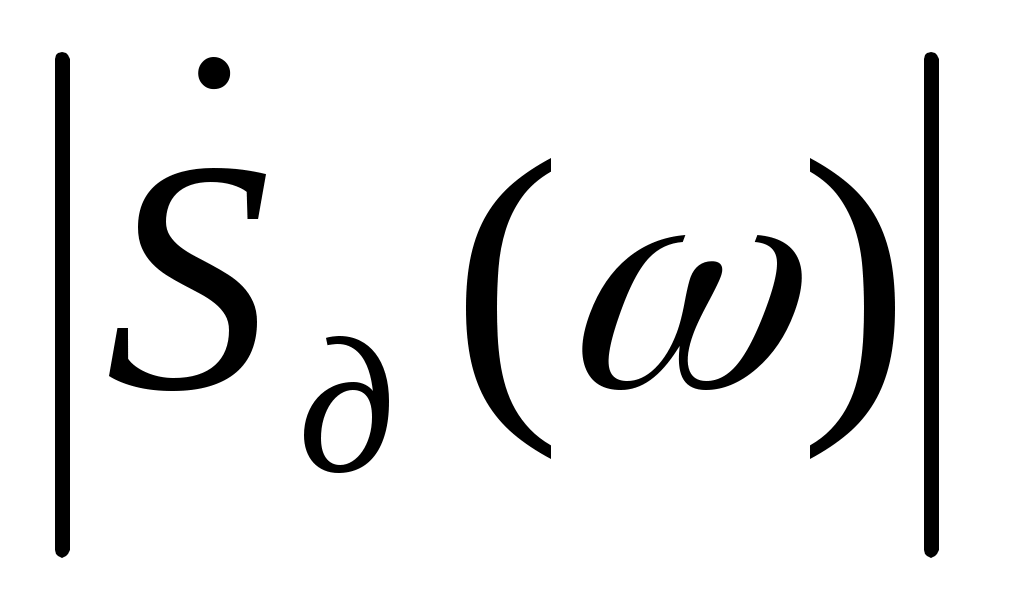, так же как и спектр аналогового сигнала s(t), непрерывный. Спектр дискретизированного сигнала по форме получается наложением спектров аналогового сигнала, сдвинутых на частоту 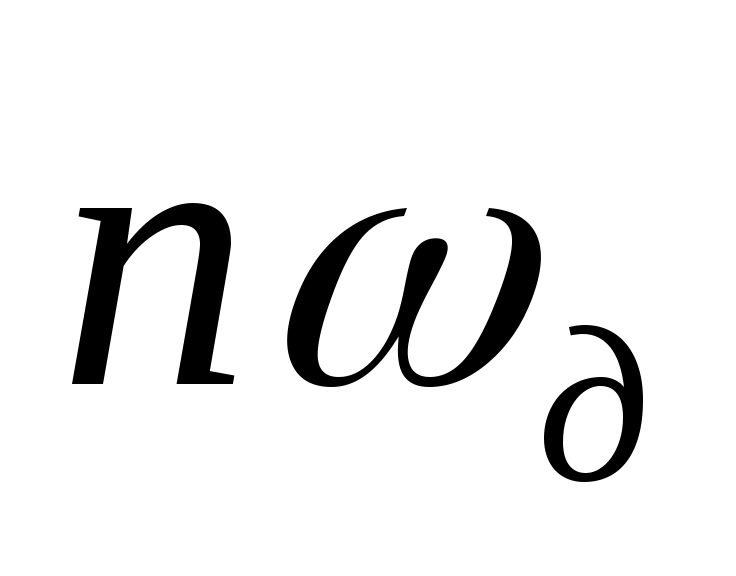(n – целое число).
  
• 
  Дискретное преобразование Фурье дало нам дискретную спектральную плотность, которая по форме полностью повторяет спектр дискретизированного сигнала. А обратное ДПФ дало нам точно значение отсчетов дискретного сигнала. Таким образом, всегда можно перейти от аналогового сигнала к дискретному и наоборот, воспользовавшись соответствующими коэффициентами Фурье.
  
• 
  Восстановление аналогового сигнала как по ДПФ, так и по Котельникову, дало нам волнообразные функции, которые полностью совпадает с восстанавливаемым сигналом в точках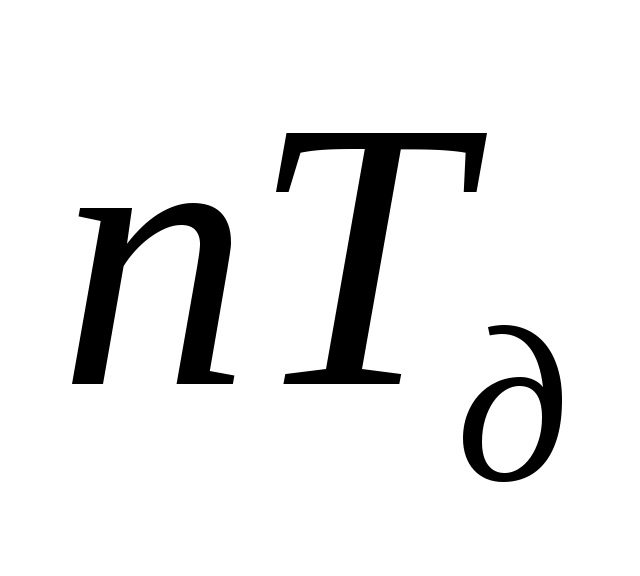 . Очевидно, что с увеличением числа отсчетом восстановление будет более точным.
  

4 Синтез цифрового фильтра по известному фильтру-прототипу

За основу синтеза цифрового фильтра возьмем аналоговый фильтр – прототип, передаточная функция и импульсная характеристика которого были рассчитаны в пункте 2.4 аналоговой части курсовой работы. Линейная цепь представлена на рисунке 1.2; ее АЧХ и ФЧХ изображены на рисунках 2.2 и 2.3, а импульсная характеристика на рисунке 2.5.

---

4.1 Дискретизация импульсной характеристики аналогового фильтра-прототипа

Для дискретизации импульсной характеристики необходимо непрерывный аргумент t заменить на дискретный . После чего пронормировать полученное выражение относительно :

(4.1)

Для нашего случая имеет следующий вид:

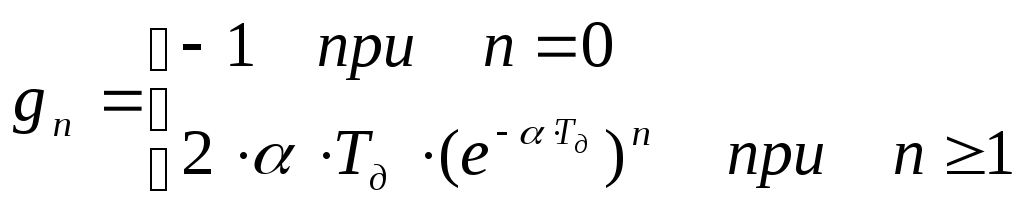(4.2)

Параметр определим по формуле:

,

(4.3)

где - частота на которой коэффициент передачи аналогового фильтра-прототипа (рис. 4.1) достигает уровня 0.05 от своего максимального значения. Вследствие того, что у нас всепропускающий фильтр, выделим его целую часть.
, выделим и построим фильтр нижних частот: .



Рисунок 4.1 АЧХ фильтра нижних частот

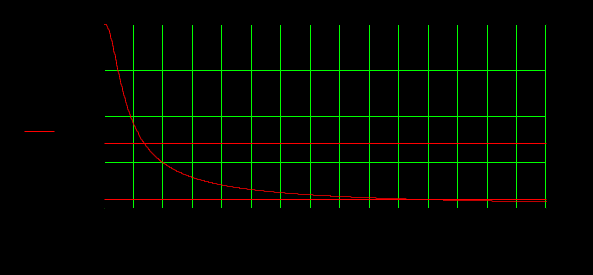
По рисунку 4.1 определим , тогда , а

На рисунке 4.2 изобразим дискретизированную импульсную характеристику, рассчитанную по формуле 4.2:

---