Добавлен: 24.04.2024
Просмотров: 110
Скачиваний: 1
СОДЕРЖАНИЕ
2 Расчет прохождения непериодического сигнала заданной формы через линейную цепь
2.1 Формирование математической модели сигнала
2.2 Представление исходного сигнала через элементарные составляющие
2.3 Расчет и построение АЧХ и ФЧХ цепи
2.4 Расчет и построение импульсной и переходной характеристик
2.5 Проверка предельных соотношений
2.6 Расчет отклика цепи операторным методом
2.7 Расчет отклика цепи временным методом
3 Дискретная обработка аналогового сигнала
3.1 Расчёт спектральной плотности сигнала и частоты среза
3.2 Дискретизация аналогового сигнала по времени
3.3 Расчет дискретной спектральной плотности
3.4 Расчет коэффициентов с помощью дискретного преобразования Фурье
3.5 ОДПФ для получения дискретного сигнала
3.6 Восстановление аналогового сигнала по ДПФ
3.7 Восстановление аналогового сигнала по ряду Котельникова
4 Синтез цифрового фильтра по известному фильтру-прототипу
4.1 Дискретизация импульсной характеристики аналогового фильтра-прототипа
4.2 Синтез трансверсального цифрового фильтра (ТЦФ) методом инвариантной импульсной характеристики.
4.3 Синтез рекурсивного цифрового фильтра (РЦФ) методом инвариантной импульсной характеристики
1 Исходные данные к курсовой работе
Исходный аналоговый сигнал представлен на рисунке 1.1. Длительность сигнала
 Рисунок 1.1 Входной аналоговый сигнал | 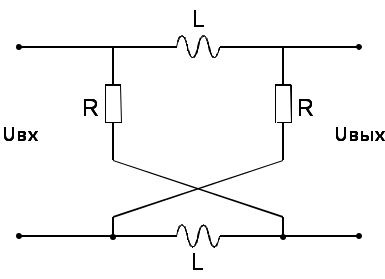 Рисунок 1.2 Исходный фильтр-прототип |
Принятые обозначения:
Скважность
2 Расчет прохождения непериодического сигнала заданной формы через линейную цепь
2.1 Формирование математической модели сигнала
Произведем поинтервальное математическое описание сигнала:
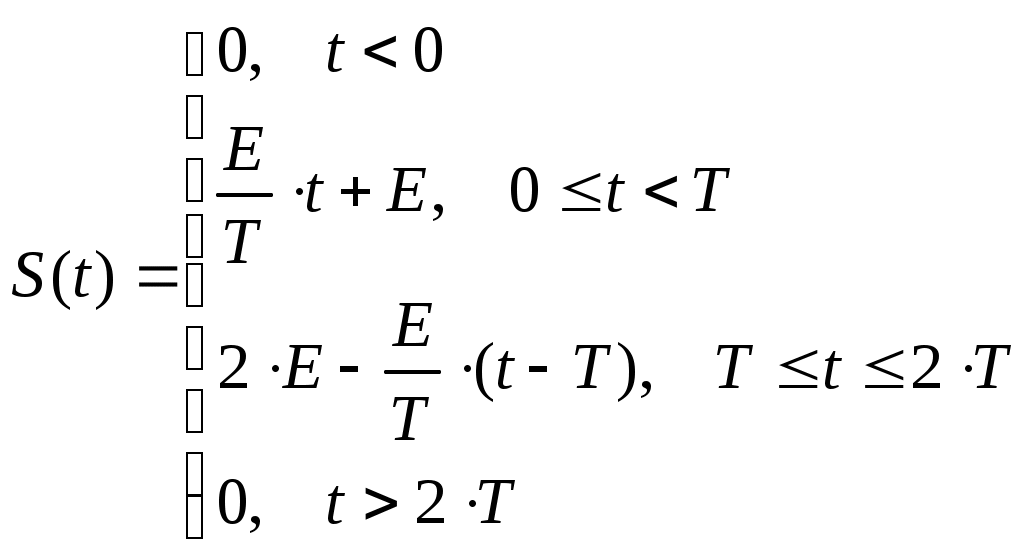 (2.1)
(2.1)2.2 Представление исходного сигнала через элементарные составляющие
Воспользуемся математическим аппаратом функции Хевисайда для разложения аналоговогосигнала на элементарные составляющие (Рисунок 2.1).
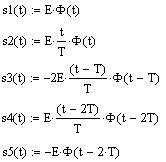 где |
|
2.3 Расчет и построение АЧХ и ФЧХ цепи
Исходная цепь представляет собой мост. Для нахождения передаточной функции цепи воспользуемся законами Ома и Кирхгофа. Запишем выражение для комплексной частотной характеристики цепи:
где
Вследствие того, что
Графики АЧХ и ФЧХ цепи представлены на рисунках 2.2 и 2.3.
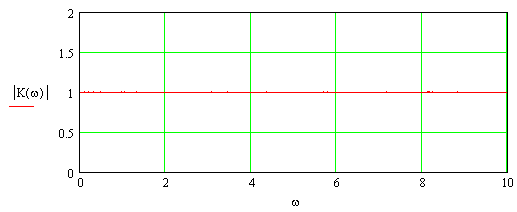
Рисунок 2.2 АЧХ аналогового фильтра-прототипа
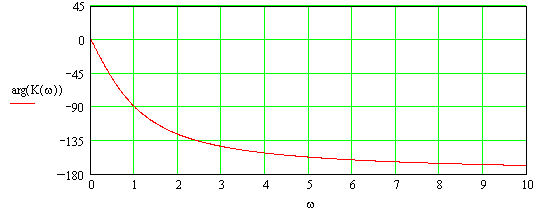
Рисунок 2.3 ФЧХ аналогового фильтра-прототипа
2.4 Расчет и построение импульсной и переходной характеристик
Для нахождения переходной характеристики цепи воспользуемся обратным преобразованием Лапласа и теорией вычетов:
Приравниваем знаменатель к нулю и найдем особые точки:
Получили два полюса кратности единица. Берем вычеты в этих точках:
Тогда общее выражение для
Для построения
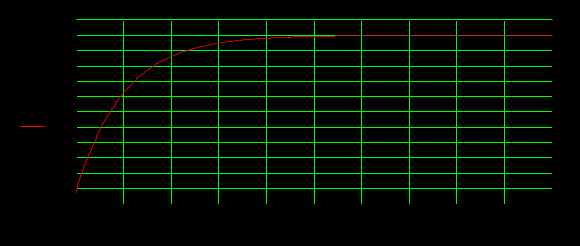
Рисунок 2.4 Переходная характеристика фильтра-прототипа
Для импульсной характеристики имеем:

Снова воспользуемся математическим аппаратом вычетов:

Общее выражение для импульсной характеристики:
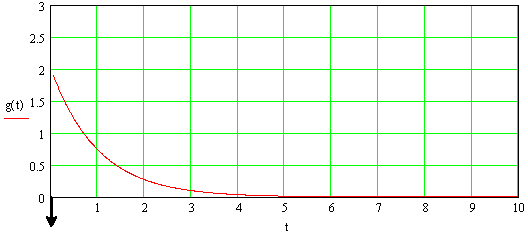
Рисунок 2.5 Импульсная характеристика фильтра-прототипа
2.5 Проверка предельных соотношений
| | Все соотношения выполняются |
Как видно из соотношений, высокие частоты соответствуют малым временам, то есть отвечают за поведение отклика в момент включения (переходный процесс), а низкие частоты — большим временам, то есть отвечают за поведение отклика в области больших времен (установившийся режим).
2.6 Расчет отклика цепи операторным методом
Выделим типовые составляющие сигнала
Найдём изображения по Лапласу от типовых составляющих:
Тогда, используя формулы (2.8) и (2.9), выходной сигнал можно представить в виде:

Построим отклик цепи при разных соотношениях
| | 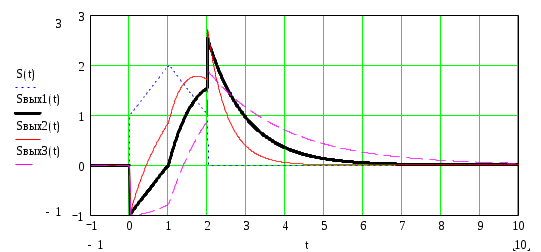 Рисунок 2.6 Отклики цепи на аналоговый сигнал, рассчитанный операторным методом |

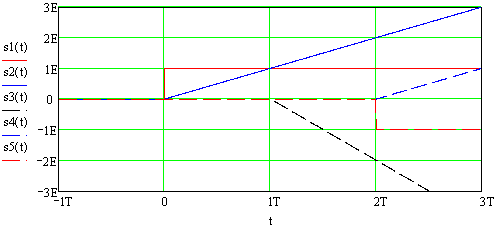 Рисунок 2.1 Элементарные составляющие аналогового сигнала
Рисунок 2.1 Элементарные составляющие аналогового сигнала
