Файл: Курсовая работа 40 страниц.doc

2.7 Расчет отклика цепи временным методом

Воспользуемся формулой Дюамеля: (2.10)
Рассчитаем отклик при помощи формулы (2.10) на каждом интервале: при 0≤ t
при T≤ t<2T и при t≥2T.

При 0≤ t При T≤ t<2T имеем:

При t≥2T имеем:



или


Построим отклик цепи при разных соотношениях :

Рисунок 2.6 Отклики цепи на аналоговый сигнал, рассчитанный временным методом

2t>2t>

---

2.8 Выводы

Как видно из полученных выше результатов, отклики цепи, рассчитанные разными методами, совпадают друг с другом. Тем самым оба метода являются практически функционирующими.

Итак, мы рассмотрели прохождение аналогового сигнала через цепь. Глядя на передаточную функцию цепи, можем сказать, что она ослабляет сигнал, и искажает его на больших частотах (малые времена) и не пропускает нулевую частоту (постоянную составляющую).

Отклик цепи определили двумя методами: операторным и методом временного интегрирования. Они оба дали одинаковый результат, но первый был более простой для расчета.

Из рисунка выходного сигнала видим, что у нас “сглаживается” поведение входного сигнала, что характерно для интегрирующей цепи, но в то же время, имеется переход через ноль (“обострение” поведения сигнала), что характерно для дифференцирующей цепи.

3 Дискретная обработка аналогового сигнала

3.1 Расчёт спектральной плотности сигнала и частоты среза

Комплексный спектр сигнала можно найти при помощи ППФ, применяя интеграл Фурье:

(3.1)

Вычислив значение интегралов, получим конечный результат:

(3.2)

Для дальнейшего удобства расчетов пронормируем спектральную плотность относительно и построим АЧХ и ФЧХ сигнала.

Используя MathCad 2001, построим АЧХ и ФЧХ сигнала:


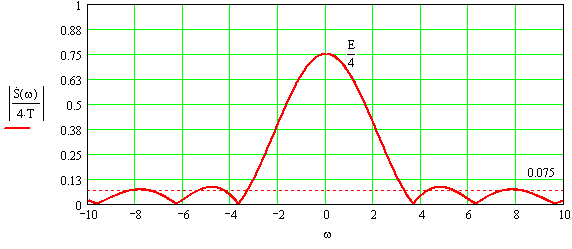
Рисунок 3.1 График модуля нормированной спектральной плотности


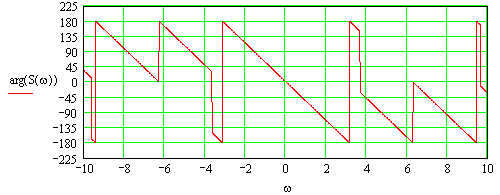
Рисунок 3.2 График ненормированного аргумента спектральной плотности

---

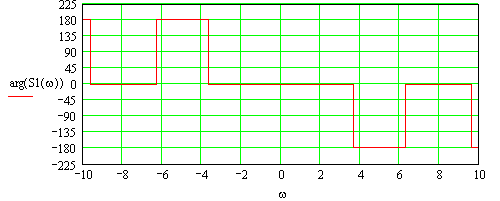
Рисунок 3.3 График нормированного аргумента спектральной плотности
График нормированного аргумента спектральной плотности получился при помощи использования теоремы сдвига, то есть вычетом из аргумента прямой.

3.2 Дискретизация аналогового сигнала по времени

Руководствуясь теоремой Котельникова, частоту дискретизации выбираем так: .

Для этого воспользуемся пороговым критерием: для частот, превышающих частоту среза, модуль спектральной плотности меньше уровня 0,1 от его максимального значения.

Частоту среза найдем из графика:
или найдем тогда .

Поскольку любой сигнал может быть описан конечным числом выборочных значений, то это число называют числом степеней свободы сигнала и находят по формуле:

. (3.3)

Дискретный сигнал получается путем замены непрерывного времени его дискретным аналогом .

По теореме Котельникова найдём дискретную последовательность , найденные отсчеты исходного импульса представим на рисунке 3.4.

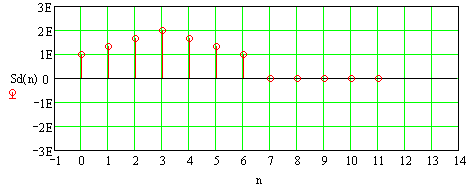
Рисунок 3.4 Отсчеты исходного аналогового импульса

(3.4)

Таким образом, дискретный сигнал задается последовательностью отсчетов вида:

. (3.5)

---

3.3 Расчет дискретной спектральной плотности

Спектральную плотность дискретной последовательности найдём по следующей формуле, применив ППФ:

(3.6)

Для облегчения расчетов произведем нормировку делением на число отсчетов, в этом случае формула приобретает упрощенный вид:

(3.7)

Графики спектральной плотности аналогового и дискретного сигнала представлены на рисунке 3.5.



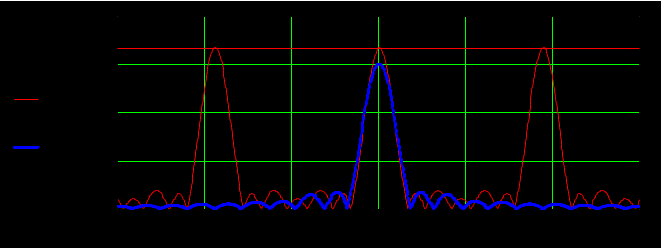
Рисунок 3.5 Спектральная плотность аналогового и дискретного сигнала
Из рисунка 3.5 видно, что модуль аналогового сигнала затухает, а дискретного является периодической функцией частоты. Амплитудный спектр дискретного сигнала расположен несколько выше аналогового, это происходит засчет наложения “хвостов” исходного спектра аналогового сигнала.

Свойства спектра дискретной последовательности. Из (3.6) следует, что спектр дискретной последовательности является периодической функцией по частоте с периодом . Периодичными по с периодом являются модуль спектра и фаза . Кроме того, модуль спектра вещественной последовательности является чётной функцией, а фаза - нечетной функцией частоты.

3.4 Расчет коэффициентов 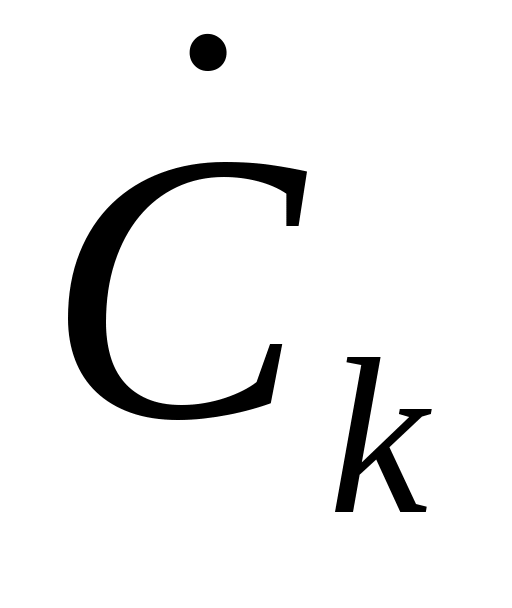с помощью дискретного преобразования Фурье

---

Найдем прямое дискретное преобразование Фурье (ПДПФ), установив однозначную связь между временными отсчетами сигнала и отсчетами его спектральной плотности. Коэффициенты рассчитаем по формуле:

, где , (3.8)

Результаты вычислений комплексных коэффициентов Фурье представлены ниже:

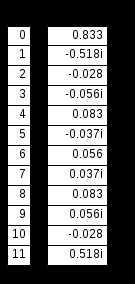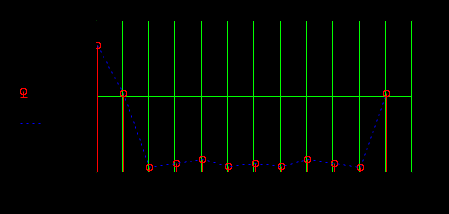Рисунок 3.6 Отсчеты спектральной плотности, полученные по ДПФ

По рисунку 3.6 видно, что нормированная по числу отсчетов спектральная плотность дискретизированного сигнала совпадает со значениями коэффициентов в точках .

Правильность вычислений проверим с помощью векторных диаграмм.



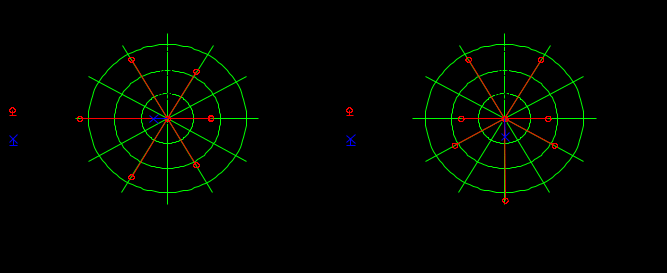
а) б)

Рисунок 3.7 Векторные диаграммы определения коэффициентов (а) и (б).



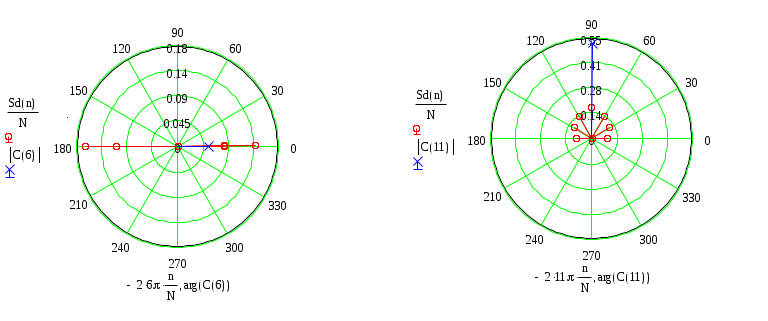
а) б)

Рисунок 3.8 Векторные диаграммы определения коэффициентов (а) и (б).
При сравнении векторных диаграмм и вычисленных значений коэффициентов видим, что проверка дала положительный результат — наши вычисления верны.

---