Добавлен: 24.04.2024
Просмотров: 112
Скачиваний: 1
СОДЕРЖАНИЕ
2 Расчет прохождения непериодического сигнала заданной формы через линейную цепь
2.1 Формирование математической модели сигнала
2.2 Представление исходного сигнала через элементарные составляющие
2.3 Расчет и построение АЧХ и ФЧХ цепи
2.4 Расчет и построение импульсной и переходной характеристик
2.5 Проверка предельных соотношений
2.6 Расчет отклика цепи операторным методом
2.7 Расчет отклика цепи временным методом
3 Дискретная обработка аналогового сигнала
3.1 Расчёт спектральной плотности сигнала и частоты среза
3.2 Дискретизация аналогового сигнала по времени
3.3 Расчет дискретной спектральной плотности
3.4 Расчет коэффициентов с помощью дискретного преобразования Фурье
3.5 ОДПФ для получения дискретного сигнала
3.6 Восстановление аналогового сигнала по ДПФ
3.7 Восстановление аналогового сигнала по ряду Котельникова
4 Синтез цифрового фильтра по известному фильтру-прототипу
4.1 Дискретизация импульсной характеристики аналогового фильтра-прототипа
4.2 Синтез трансверсального цифрового фильтра (ТЦФ) методом инвариантной импульсной характеристики.
4.3 Синтез рекурсивного цифрового фильтра (РЦФ) методом инвариантной импульсной характеристики
Рисунок 4.2 Дискретизированная импульсная характеристика
4.2 Синтез трансверсального цифрового фильтра (ТЦФ) методом инвариантной импульсной характеристики.
Трансервальный ЦФ имеет конечную импульсную характеристику (КИХ-фильтр).
Для построения КИХ - фильтра необходимо взять конечное число М нормированных отсчетов импульсной характеристики, число М определяет порядок фильтра. Для его нахождения воспользуемся пороговым критерием (по уровню 0.05 от максимального значения). В соответствии с рисунком 4.2: пороговый критерий определяет порядок фильтра М=7.
Алгоритм работы ТЦФ представлен формулой (4.4):
| | (4.4) |
где коэффициенты
Таблица 4.1 – Коэффициенты
| | | | | | | | |
| -1 | 0,268 | 0,229 | 0.196 | 0.168 | 0.143 | 0.122 | 0.105 |
Нулевой отсчет занят
| Изобразим структуру ТЦФ фильтра: | 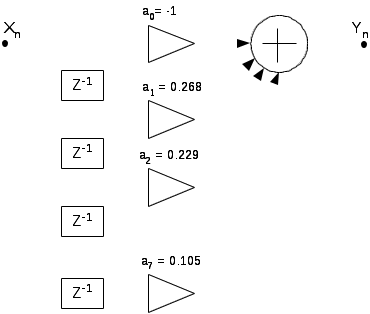 |
Рисунок 4.3 Структурная схема трансверсального ЦФ
Системная функция трансверсального ЦФ представляет собой сумму следующего вида:
| | (4.5) |
Для того, чтобы от системной функции перейти к амплитудно-частотной характеристике, в
Изобразим на рисунках 4.4 и 4.5 АЧХ и ФЧХ фильтра, ожидая при этом, что они будут периодическими функциями частоты.
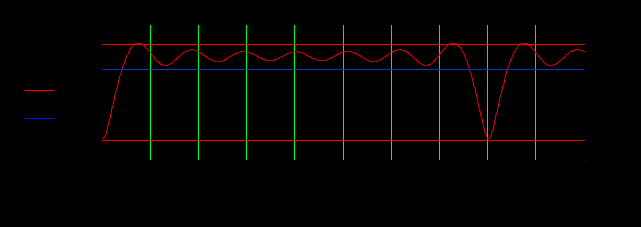
Рисунок 4.4 АЧХ трансверсального цифрового фильтра
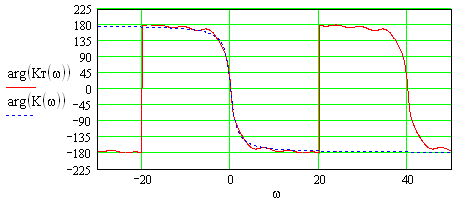
Рисунок 4.5 ФЧХ трансверсального цифрового фильтра
Пульсации АЧХ трансервального фильтра объясняются ограничением импульсной характеристики во времени М=7.
4.3 Синтез рекурсивного цифрового фильтра (РЦФ) методом инвариантной импульсной характеристики
Рекурсивный цифровой фильтр работает по следующему алгоритму:
| | (4.6) |
Здесь выходные отсчеты
Цифровой фильтр с бесконечной импульсной характеристикой (БИХ - фильтр) реализуется при учете в дискретной импульсной характеристике бесконечного числа слагаемых. При этом мы имеем бесконечно убывающую геометрическую прогрессию, сворачивая которую, получим системную функцию ЦФ канонического вида,
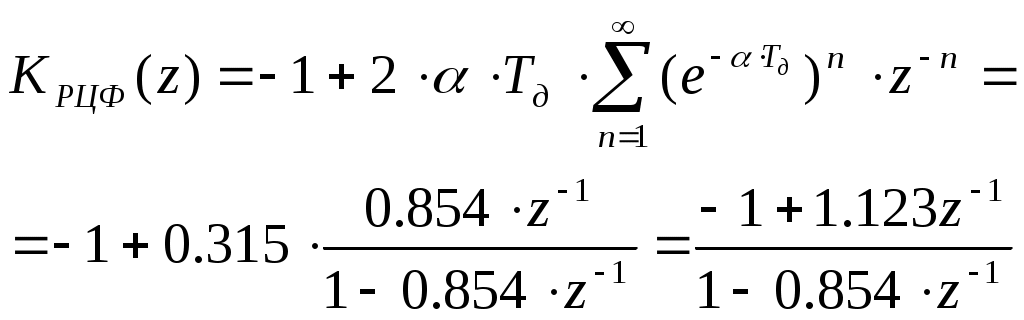 | (4.7) |
И теперь можем записать:
Порядок трансверсальной части М=1, рекурсивной – N=1,
Алгоритм работы РЦФ:
Изобразим структуру рекурсивного фильтра:
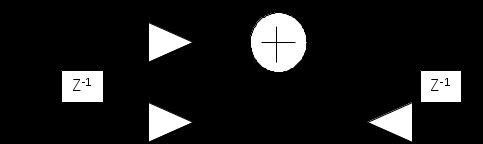
Рисунок 4.6 Структурная схема рекурсивного цифрового фильтра
Заменяя в выражении (4.7)
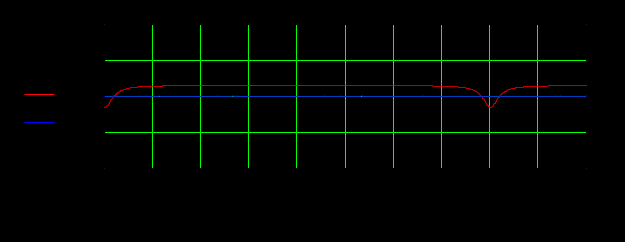 Рисунок 4.7 АЧХ рекурсивного цифрового фильтра
Рисунок 4.7 АЧХ рекурсивного цифрового фильтра-
Расчёт цифровых фильтров.
-
Расчёт передаточной функции цепи.
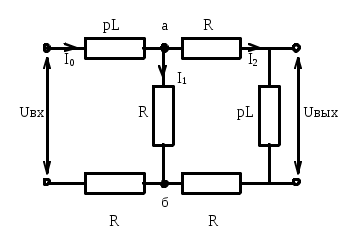
Проведём качественный анализ АЧХ передаточной функции.
Так как выходное напряжение полностью определяется второй индуктивностью в цепи, то при
Расчёт передаточной функции K(p) проведем по известной формуле
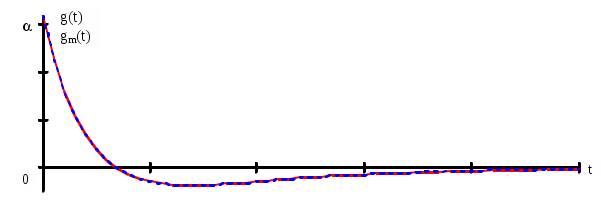
Импульсная характеристика, найденная вручную полностью совпала с найденной c помощью MathCad6.0+.
3.3. Дискретизация импульсной характеристики цепи.
Определим время дискретизации
Продискретизируем время
Подставим в выражение (3.2.3) получившееся выражение (3.3.2)

