ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 28.04.2024
Просмотров: 71
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Лабораторная работа «Исследование устойчивости и качества линейных систем управления».
Лабораторная работа «Исследование влияние нулей и полюсов передаточной функции на свойства системы».
Лабораторная работа «Исследование дискретных линейных систем»
Лабораторная работа «Исследование адаптивной системы управления»
Лабораторная работа «Исследование оптимальных по быстродействию процессов»
Лабораторная работа «Исследование системы экстремального управления».
-
-
Содержание отчета
-
-
Структурные схемы исследуемых систем. -
Корневые корни исследуемых систем. -
кривые переходных процессов. -
Выводы.
-
Дискретные системы- 1 2 3 4 5 6 7 8 9 ... 12
-
Лабораторная работа «Исследование дискретных линейных систем»
-
-
Цель работы: Целью работы является изучение характерных особенностей поведения линейных дискретных систем. -
Теоретическая часть
-
-
Дискретной системой называется такая система, которая кроме непрерывных звеньев содержит хотя бы одно импульсное звено, преобразующее непрерывный сигнал в последовательность импульсов определенной формы. При этом импульсное звено представляется в виде двух частей: идеального ключа и формирующего элемента, называемого экстраполятором.
-

-
Рисунок 2.1.1 – импульсное звено -
-
Числа, составляющие последовательность, являются значениями сигнала в отдельные дискретные моменты времени и называются отсчетами сигнала. Как правило, отсчеты берутся через равные промежутки времени T, называемые периодом дискретизации (шагом дискретизации). Последовательность импульсов на выходе экстраполятора можно описать функцией: -
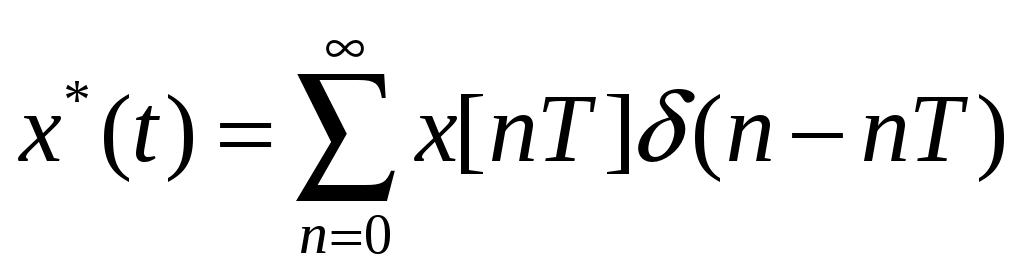
-
Экстраполятор формирует реальные импульсы заданной формы. Обычно импульсный элемент в дискретных системах расположен после сравнивающего устройства, и структурная схема имеет вид: -
-
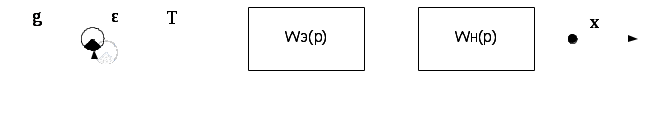
-
Рисунок 2.1.2 – структура дискретной системы -
-
Wн(р) - передаточная функция непрерывной части -
Wэ(р) - передаточная функция экстраполятора -
Экстраполятор и непрерывная часть образуют приведенную непрерывную часть с передаточной функцией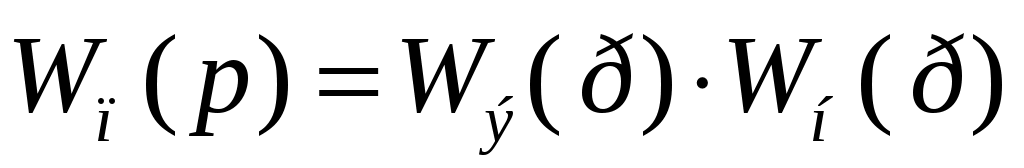 .
. -
Вид передаточной функции Wэ(Р) определяется формой импульсов на выходе экстраполятора. Наиболее часто в дискретных системах применимы экстраполяторы, формирующие короткие прямоугольные импульсы длительностью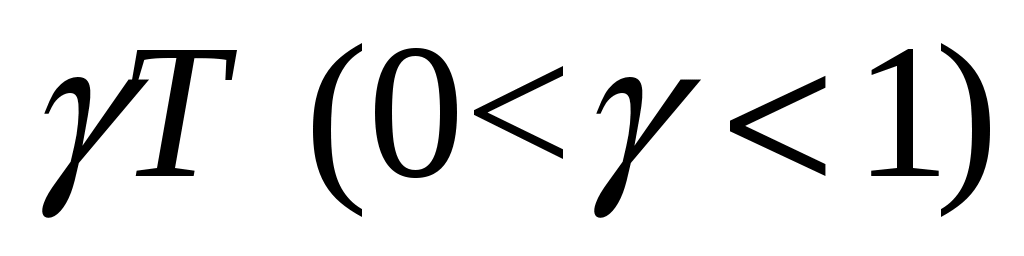 и прямоугольные импульсы, длительность которых равна периоду Т(γ=1).
и прямоугольные импульсы, длительность которых равна периоду Т(γ=1). -
В первом случае имеем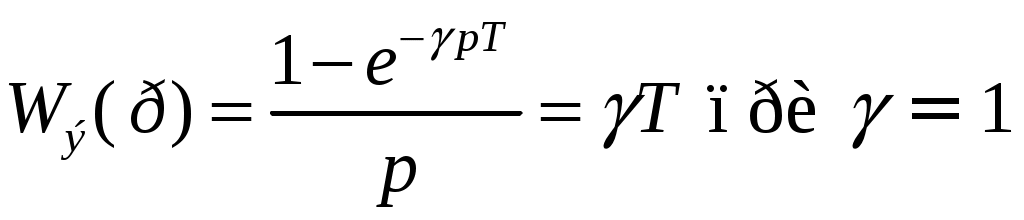
-
Во втором случае имеем экстраполятор нулевого порядка с передаточной функцией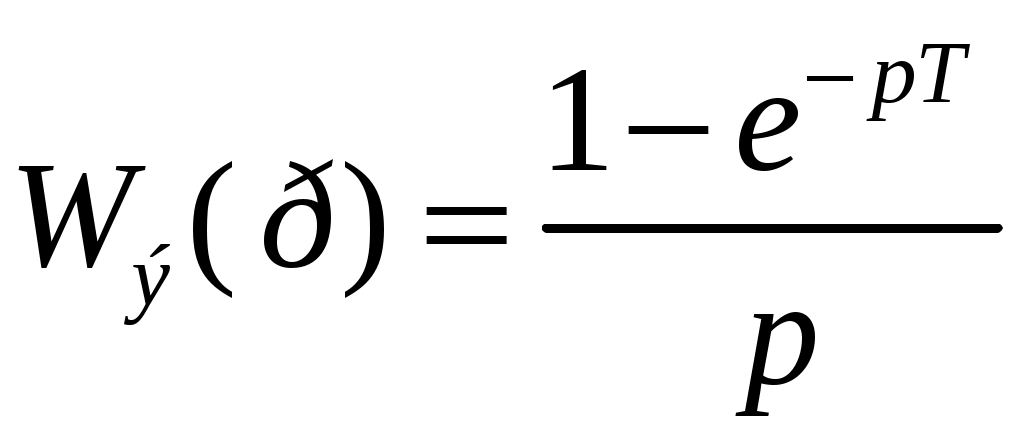
-
Для непрерывной функции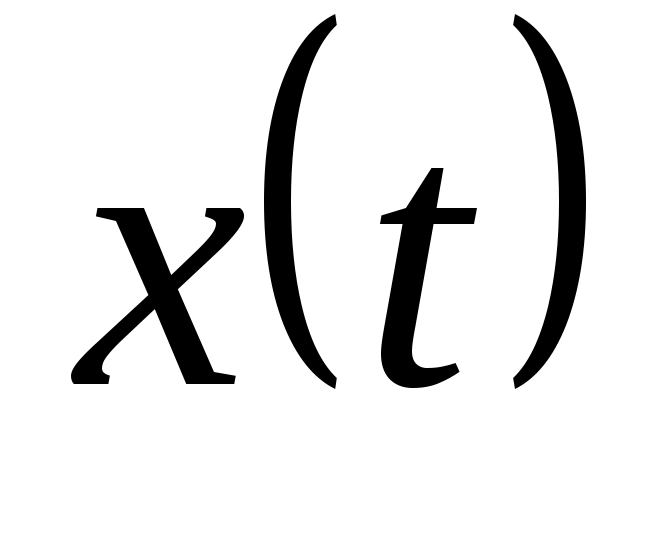 существует преобразование Лапласа
существует преобразование Лапласа 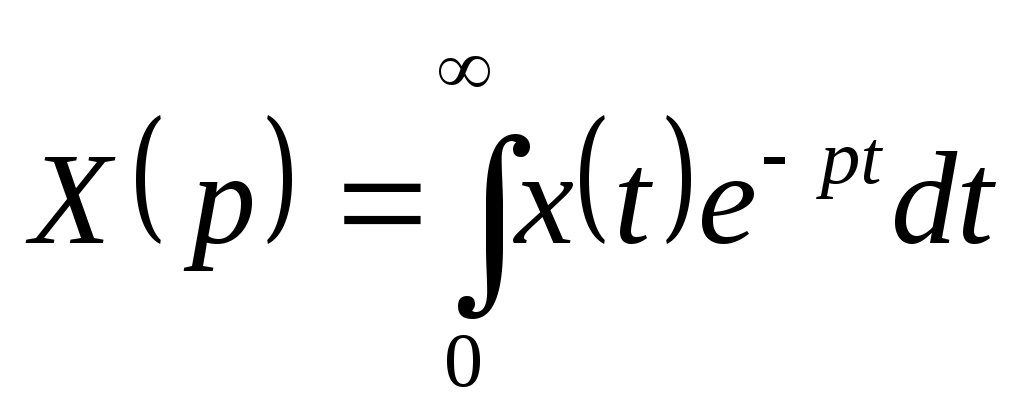 . При переходе к дискретным функциям
. При переходе к дискретным функциям 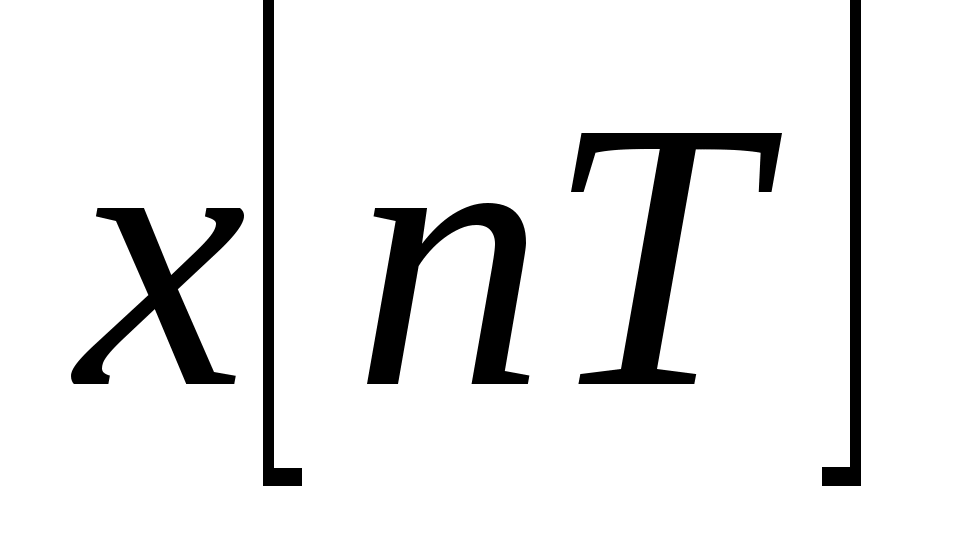 имеем:
имеем: -
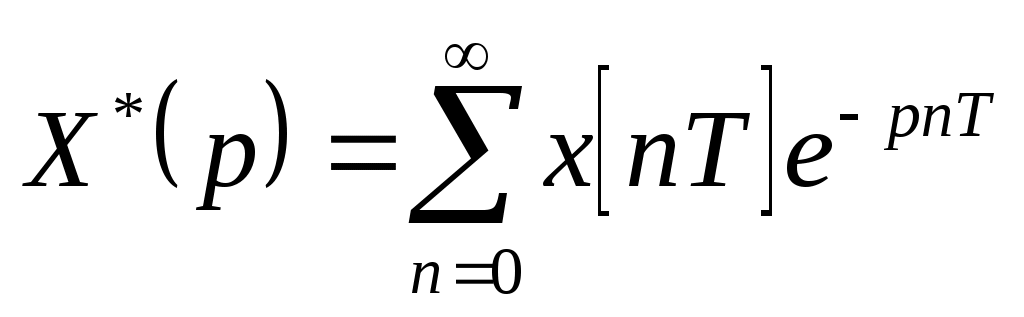 – дискретное преобразование Лапласа.
– дискретное преобразование Лапласа. -
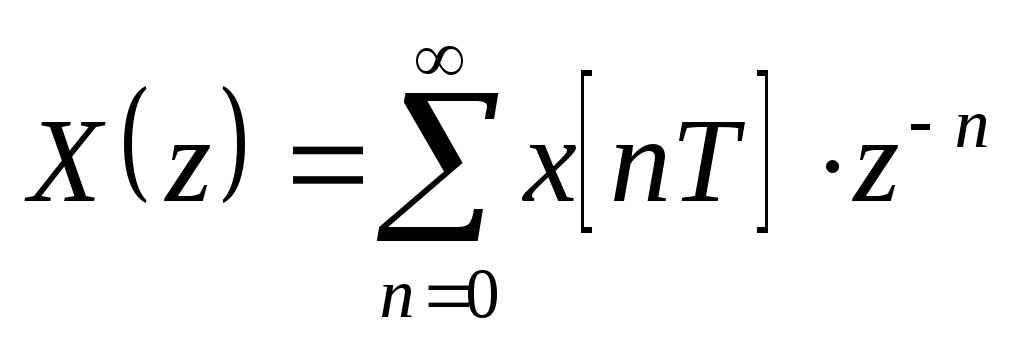 , где
, где 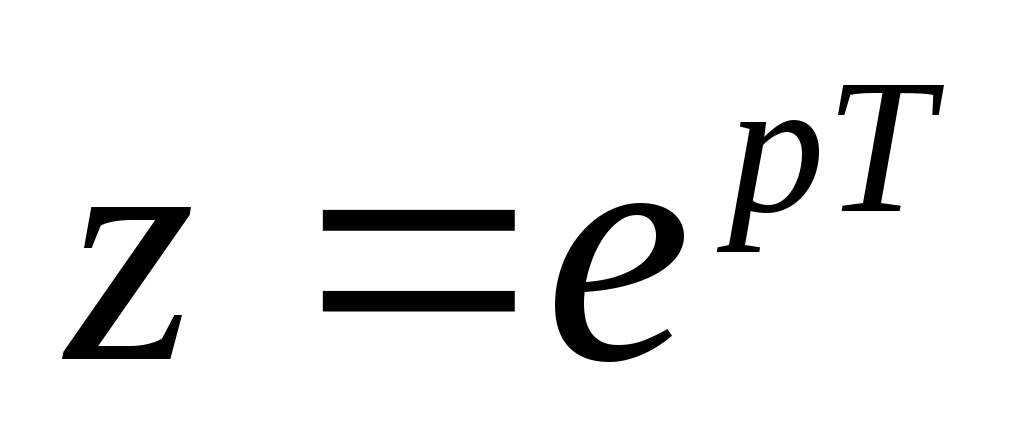 - оператор запаздывания или опережения на один такт.
- оператор запаздывания или опережения на один такт. -
При этом под дискретной передаточной функцией звена или системы понимается отношение Z- преобразований выходной и входной величин. Для рассматриваемой структурной схемы рисунок2.6.2. имеем -
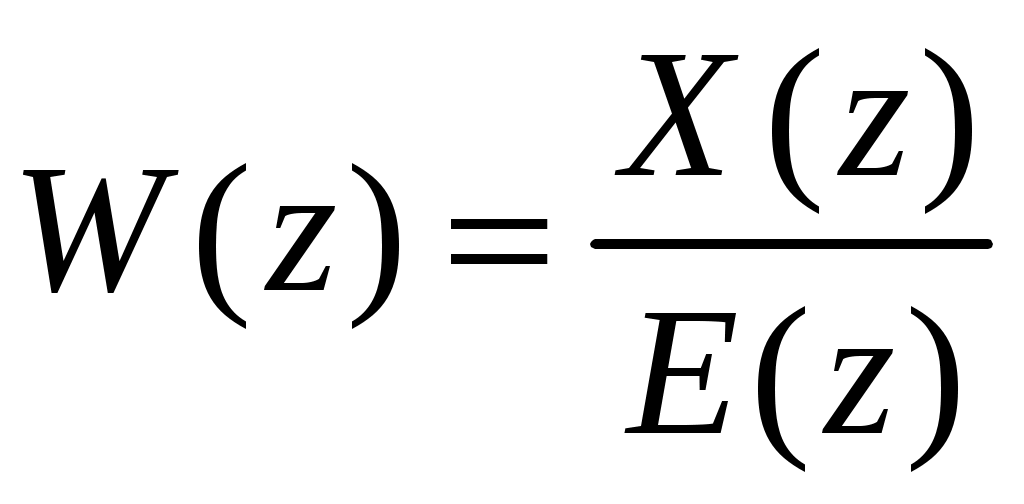 - передаточная функция разомкнутой системы
- передаточная функция разомкнутой системы -
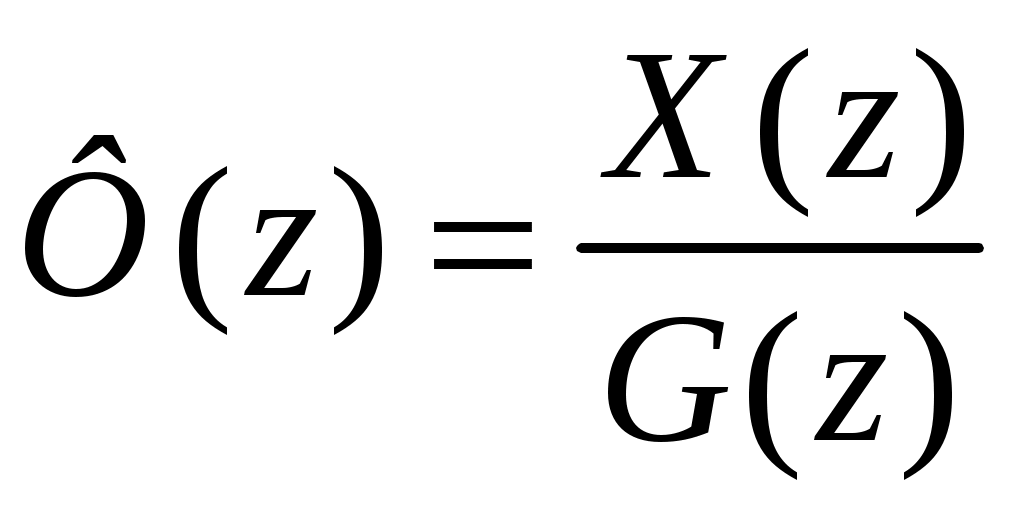 - передаточная функция разомкнутой системы
- передаточная функция разомкнутой системы -
W(z) можно получить по известной Wп(р). Так ,например, для экстраполятора с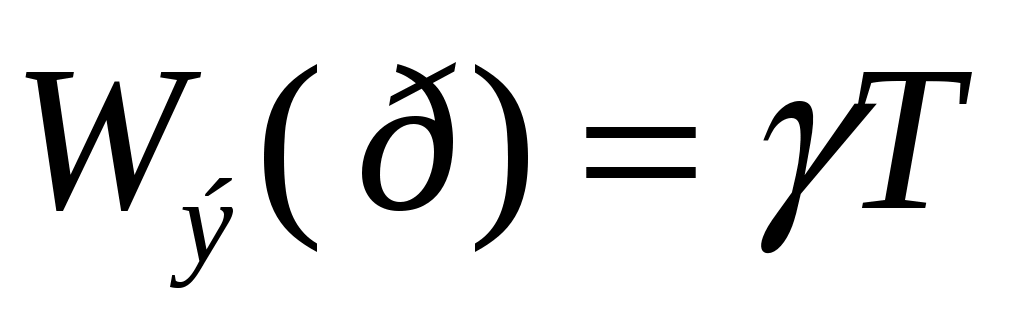 имеем
имеем 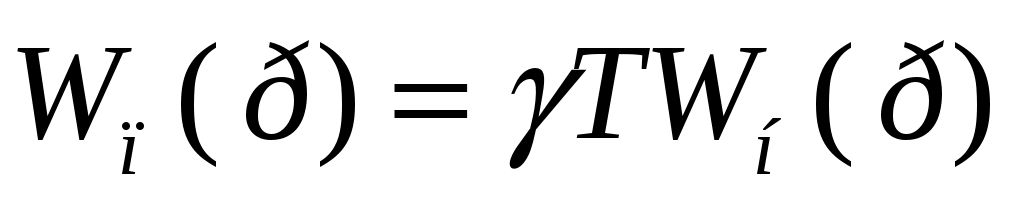 .
. -
Определим Z{Wп(р)} Z - преобразование для γTW(р)путем разложения ее на простые дроби. Z - преобразование простых дробей известны и сведены в таблицы. Для экстраполятора нулевого порядка имеем -
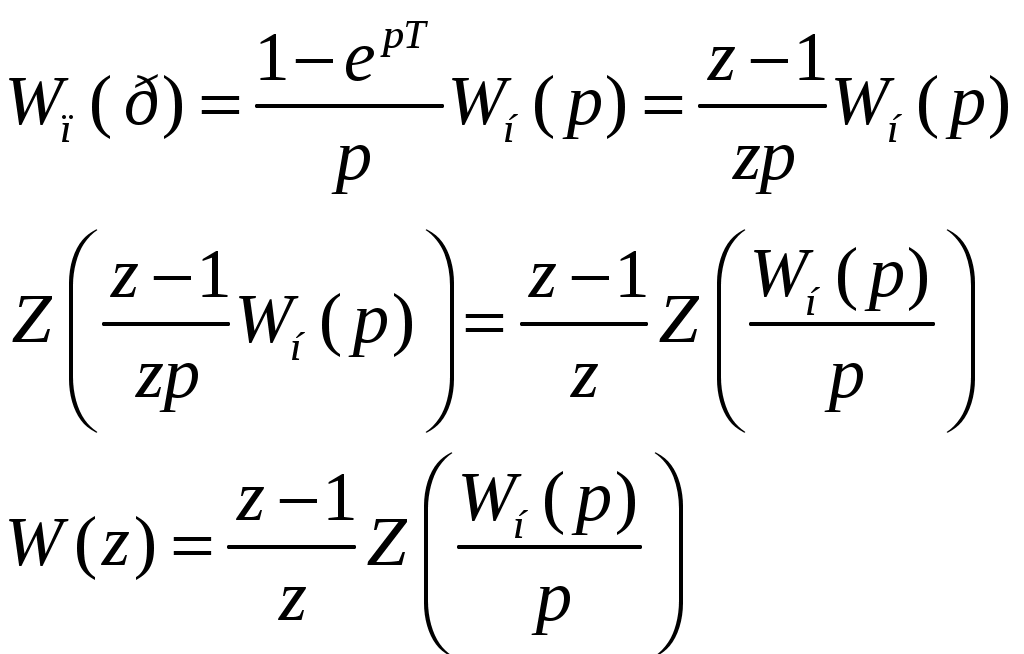
-
Приведем z- преобразования некоторых простых дробей -
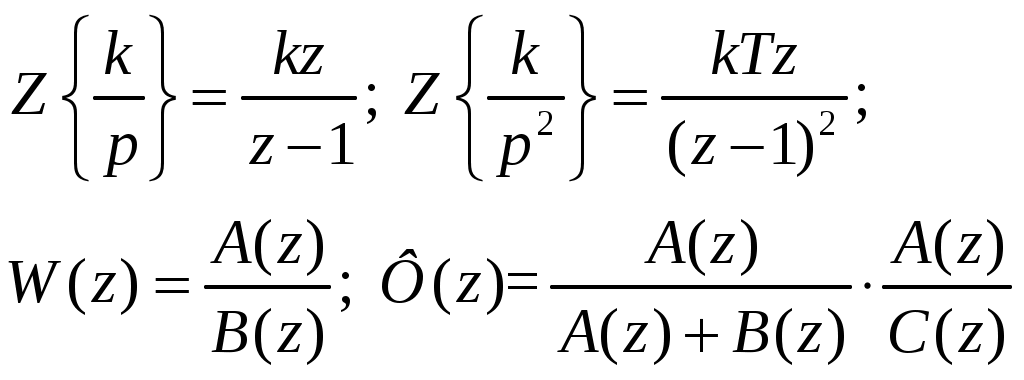 ,
, -
Где A(z) - полином от z - системы l; -
В(z) - полином от z - системы m; (m< -
C(z) - характеристическое уравнение. -
Для обеспечения устойчивости необходимо, чтобы корни характеристического уравнения Zi не превышали по модулю единицу (|Zi|<1); -
Выходной процесс может быть получен по известной Ф(z) и z- преобразованию входного сигнала Х(z)=Ф(z)*G(z). -
Можно получить переходный процесс путем деления числителя на знаменатель. При этом коэффициенты при z-i полученного ряда будут значения x(iT). -
Характерной особенностью дискретных систем является возможность получения переходных процессов конечной длительности. Это достигается при выполнении условия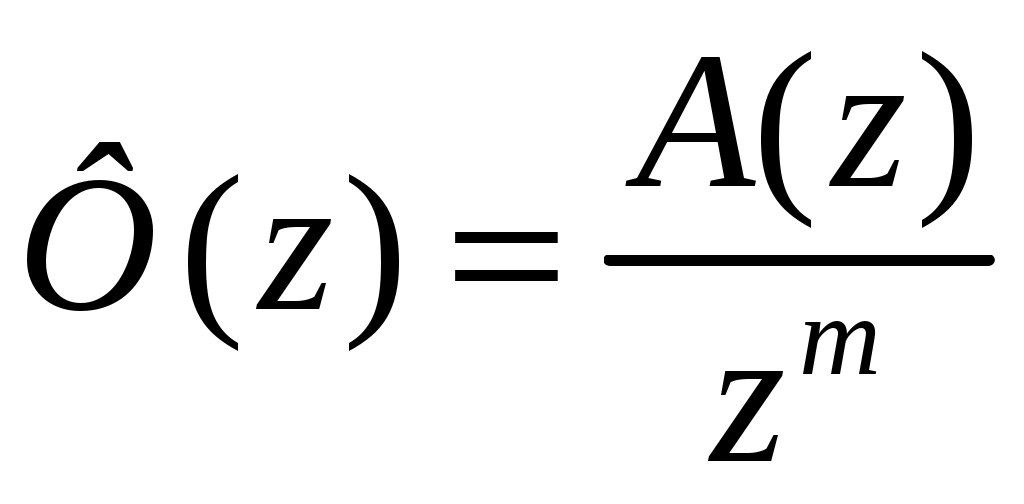 . Очевидно, что при деления получим ряд с ограниченным числовым слагаемых m, равным порядку системы.
. Очевидно, что при деления получим ряд с ограниченным числовым слагаемых m, равным порядку системы. -
-
Порядок выполнения работы
-
Варианты заданий:
№ варианта
параметры
1
2
3
4
5
6
7
8
9
10
k
1
2
1,2
5
4
3,5
9
5,7
6,8
8
γ
0,1
0,2
0,1
0,3
0,1
0,2
0,3
0,2
0,1
0,3
-
-
-
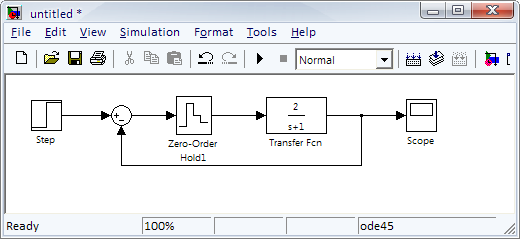
Собрать структурную схему, как показано на рисунке 3
-
-
-
Рисунок 2.1.3 – структурная схема исследуемой системы
-
В реализованной схеме рисунок3, экстраполятор нулевого порядка,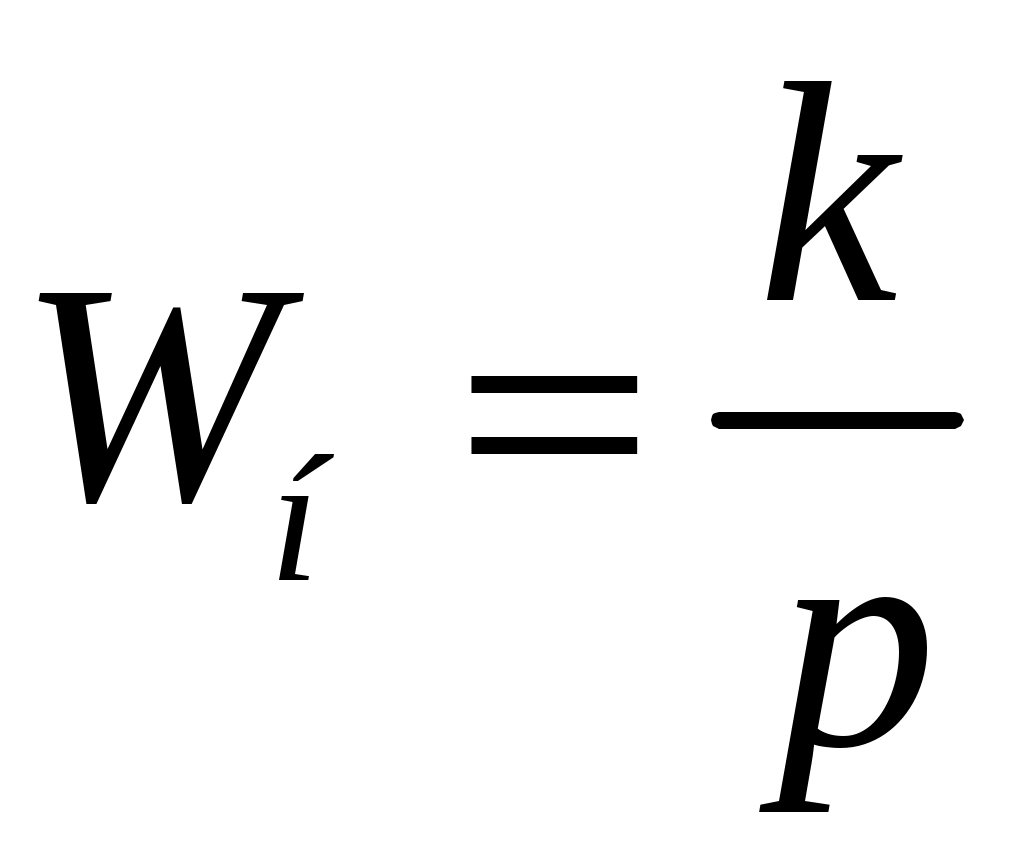 , Т=1.
, Т=1. -
Получить переходные процессы в системе при g(t) = 1(t) для различных k (-k,0.1,k). -
Определить экспериментально значение k, при котором процесс заканчивается за 1 такт дискретности; и k исходя из условия нахождения системы на границе устойчивости. -
Сравнить с расчетными значениями. -
Повторить п.п.3 учитывая что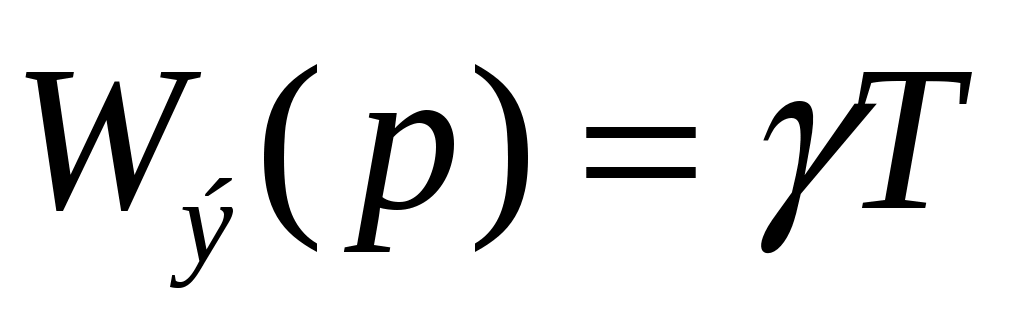 , γ – согласно варианту задания.
, γ – согласно варианту задания.
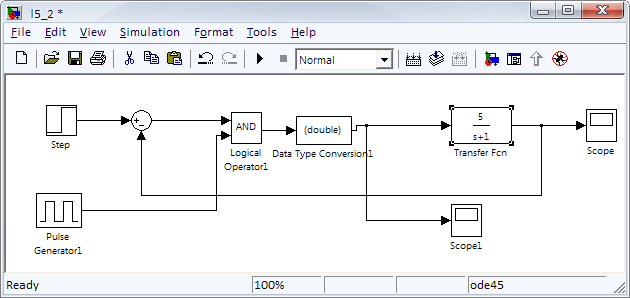
Схема для исследования будет иметь вид:
-
-
-
Рисунок 2.1.4 – структурная схема исследуемой системы
-
Повторить п.п. 1-4 для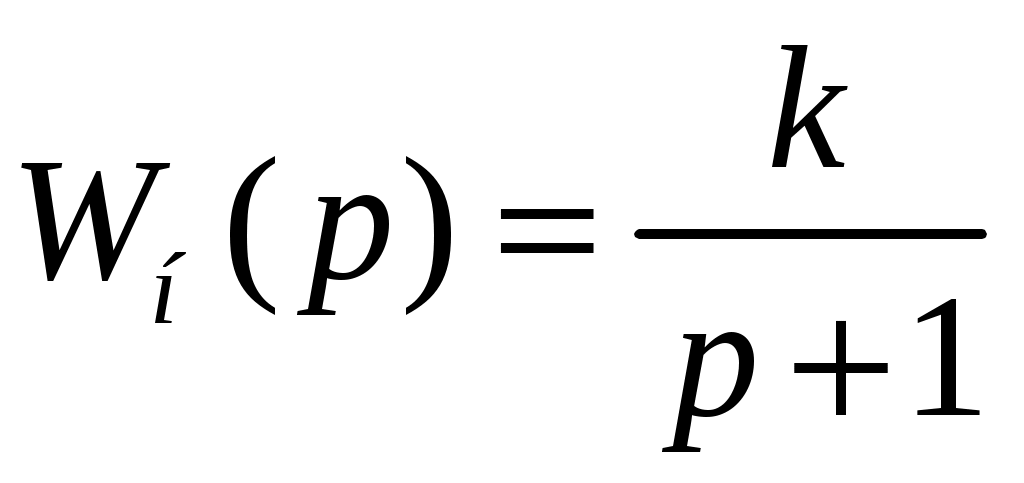
-
Содержание отчета
-
-
Структурные схемы дискретных систем с определением расчетным путем W(z), Ф(z). -
Графики переходных процессов исследуемых систем. -
Расчетные данные и сравнение их с экспериментальными.
-
Контрольные вопросы
-
Что такое дискретная система? -
Что такое частота Найквиста? -
Что такое решетчатая функция? -
Назовите виды квантования сигнала, в чем их отличительная особенность? -
Назовите виды экстраполяторов их назначение. -
Сформулируйте теорему Котельникова. Покажите ее применение на примете разложения произвольного сигнала в спектр.
- 1 2 3 4 5 6 7 8 9 ... 12
Нелинейные системы
-
Лабораторная работа «Исследование свойств систем на фазовой плоскости»
-
-
Цель работы: Экспериментальное изучение методов фазовых траекторий для оценки свойств линейных и нелинейных систем управления. -
Теоретическая часть
-
Уравнение свободного движения системы в общем случае имеет вид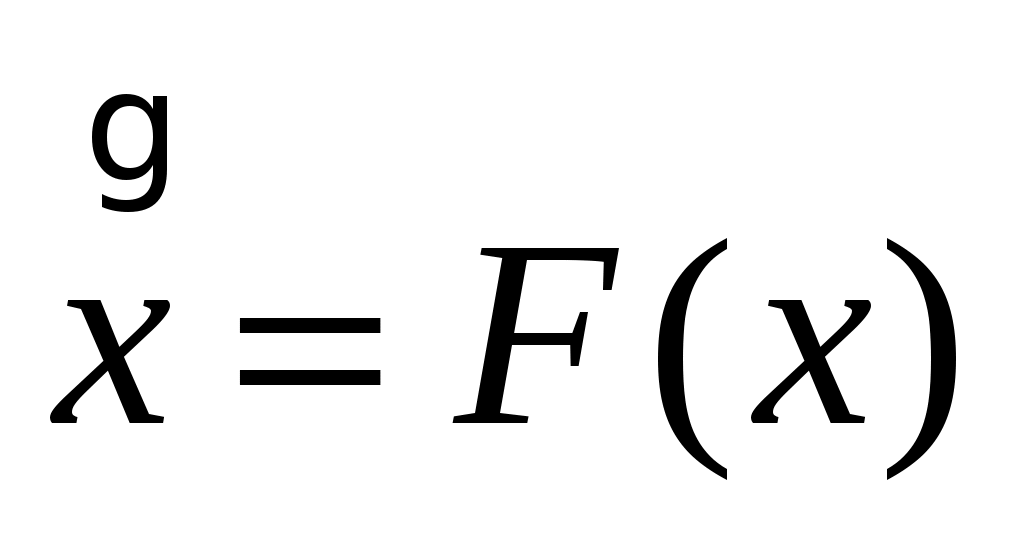 , где х - вектор состояния системы, F - в общем случае нелинейная вектор функция. Используя геометрическое представление, получим, что с течением времени вектор свободного движения x(t) будет занимать различное положения в пространстве состояний. Геометрическое место концов вектора x(t) называют фазовой траекторией системы, а их совокупность фазовым портретом.
, где х - вектор состояния системы, F - в общем случае нелинейная вектор функция. Используя геометрическое представление, получим, что с течением времени вектор свободного движения x(t) будет занимать различное положения в пространстве состояний. Геометрическое место концов вектора x(t) называют фазовой траекторией системы, а их совокупность фазовым портретом. -
Различному характеру движений в системе соответствует различный вид фазовых траекторий, что позволяет использовать фазовые траектории для исследования качества процессов в системе. Наиболее наглядно эта связь проявляется в системах второго порядка, когда пространство состояний является двумерным и геометрически представляется на плоскости. При этом обычно выбирают такую систему координат (базис пространства), что по оси абсцисс откладывается Х1 - отклонение системы от положения равновесия, а по оси ординат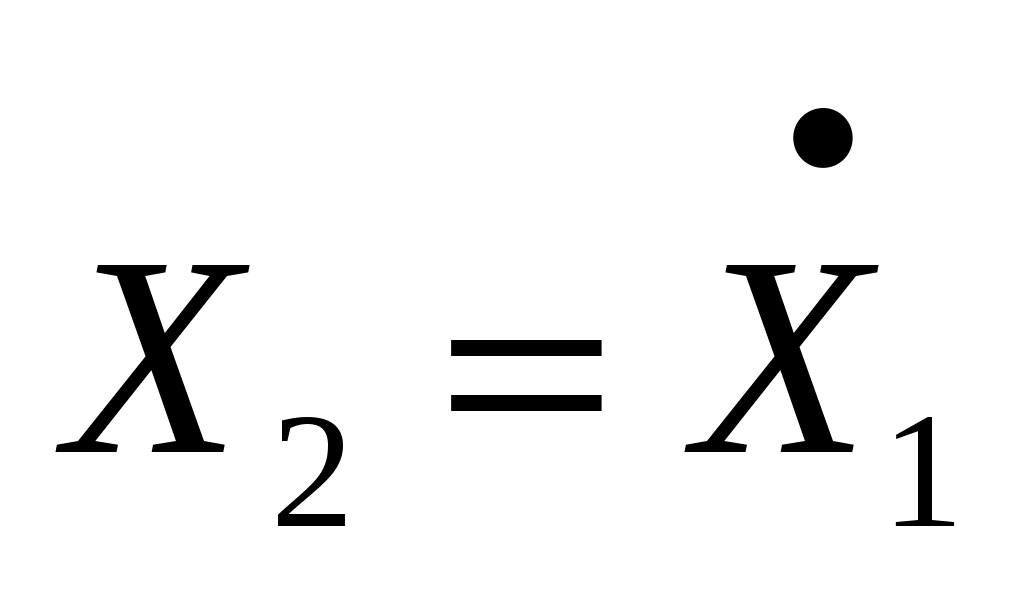 - скорость этого отклонения.
- скорость этого отклонения. -
Получить уравнения фазовых траекторий на плоскости можно, исключив время в уравнениях системы, записанных в нормальной форме Коши, следующим образом: -
Пусть система описывается уравнением -
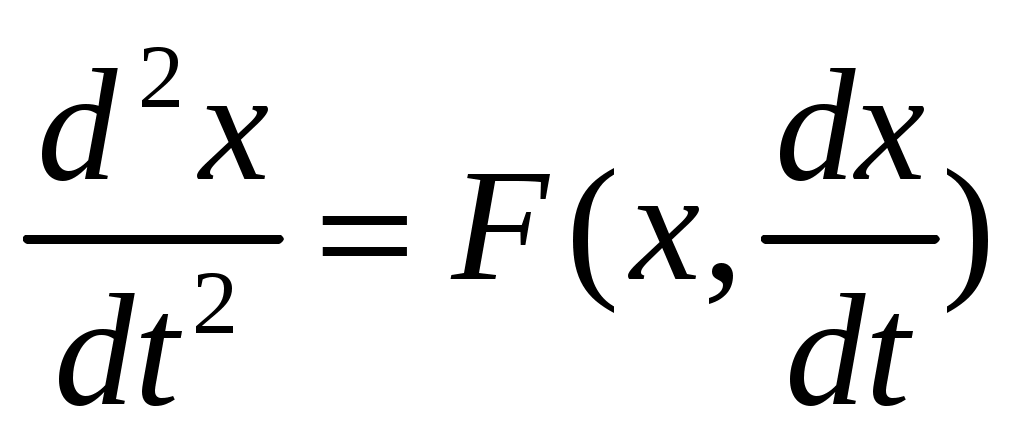
-
Обозначим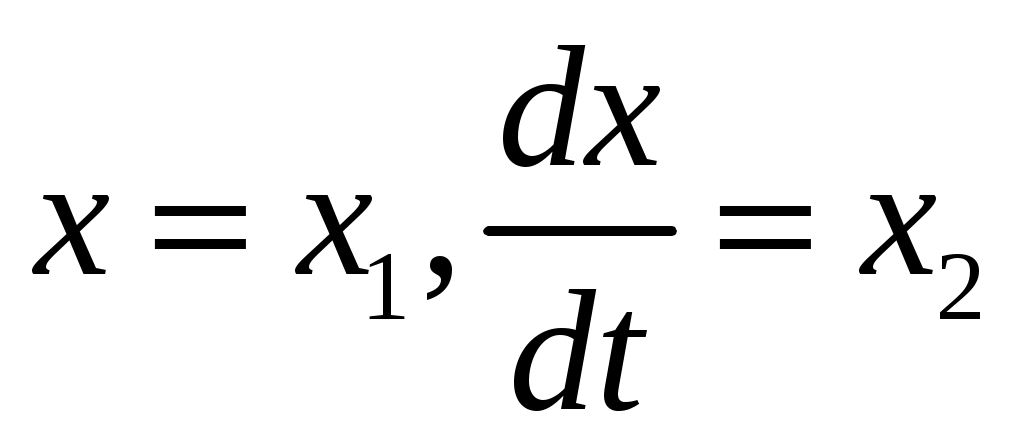 , получим:
, получим: -
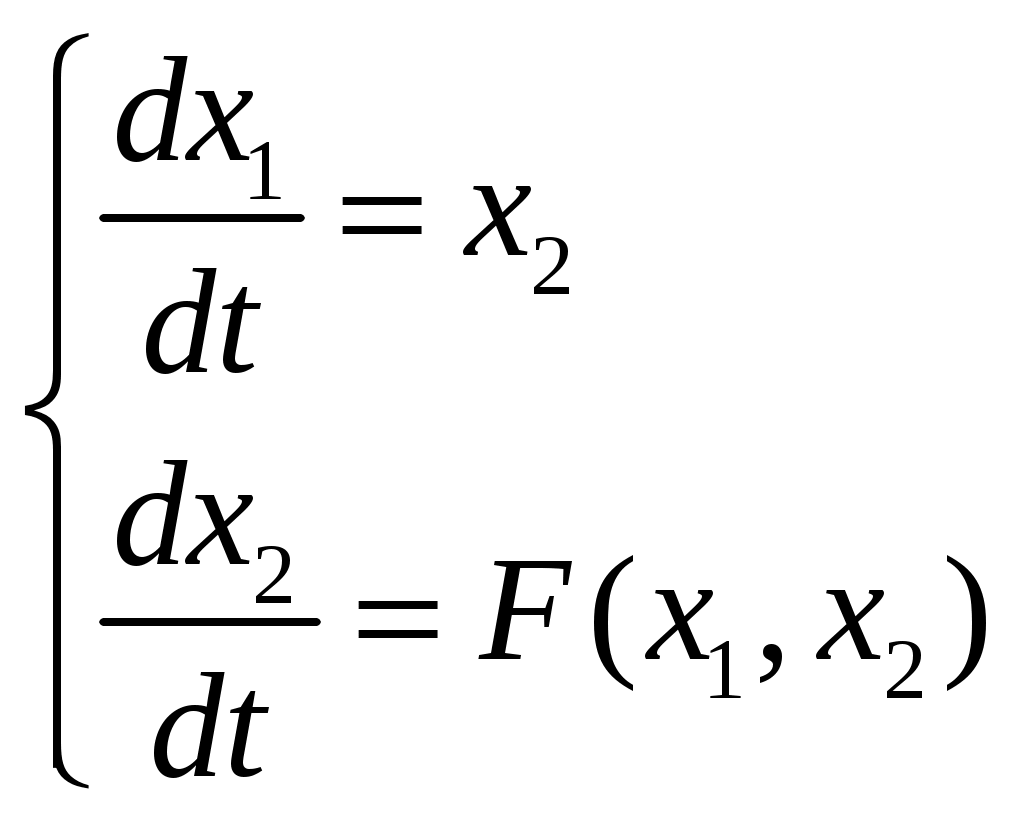
-
Поделив одно уравнение на другое, получим -
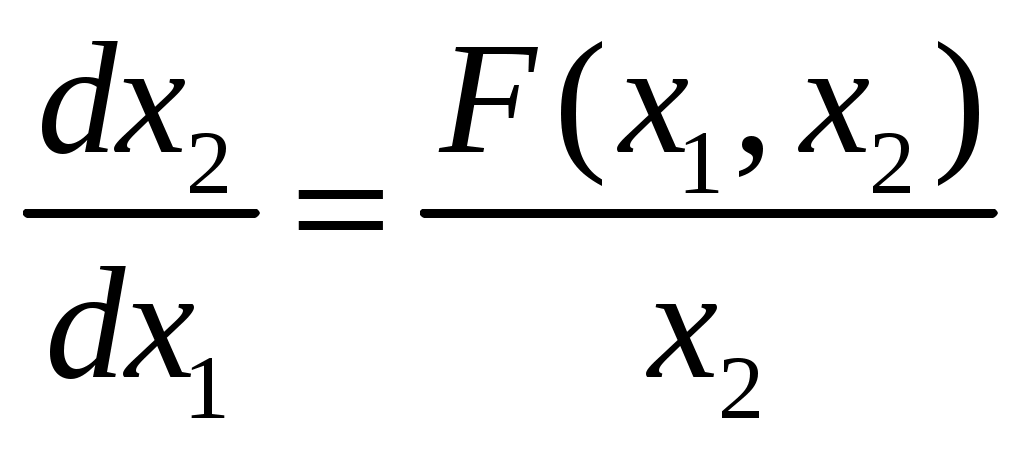
-
Решая, данное нелинейное дифференциальное уравнение либо аналитически, либо одним из приближенных методов, получим уравнение фазовой траектории для заданных начальных условий в виде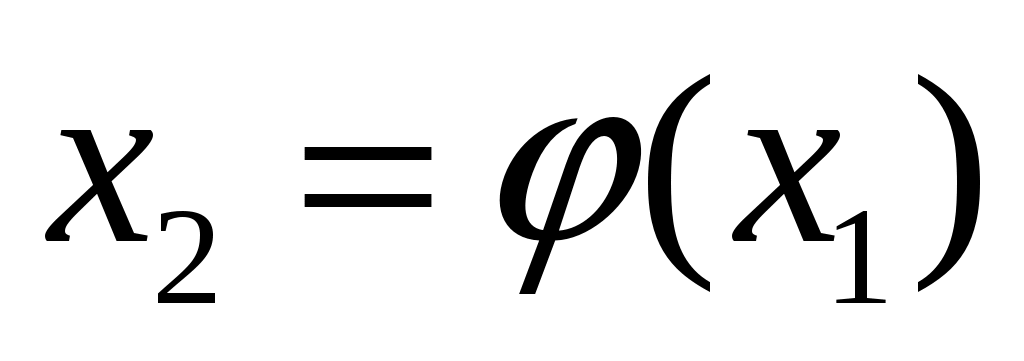
-
-
Порядок выполнения работы
-
Варианты заданий: -
№
варианта
нелинейный
элемент
a
b
c
d
1
реле
[-1;1]
0
-
-
2
реле с гистерезисом
[-0.5;0.5]
[-1;1]
-
-
3
ограничетель
-
-
-
[-0,5;0,5]
4
зона нечувствит.
-
-
[-0,5;0,5]
-
5
реле с гистерезисом
[-0.3;0.3]
[-0,5;0,5]
-
-
6
реле
[-0.5;0.5]
-0,5
-
-
7
ограничетель
-
-
-
[-0,75;0,75
8
зона нечувствит.
-
-
[-0,2;0,2]
-
9
реле с гистерезисом
[-0,75;0,75]
[-0,25;0,25]
-
-
10
зона нечувствит.
-
-
[-0,35;0,35]
-
-
-
а – уровни ограничения -
b – пороги включения и выключения -
с – начало и конец зоны нечувствительности -
d – пороги ограничения -
-
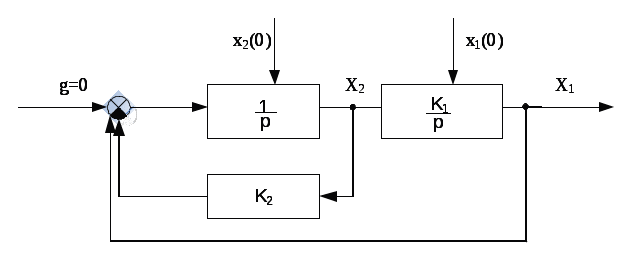
Собрать структурную схему, как показано на рисунке 3.1.1
-
-
Рисунок 3.1.1 – Структурная схема линейной системы -
-
В системе MatLab она может выглядеть следующим образом
-
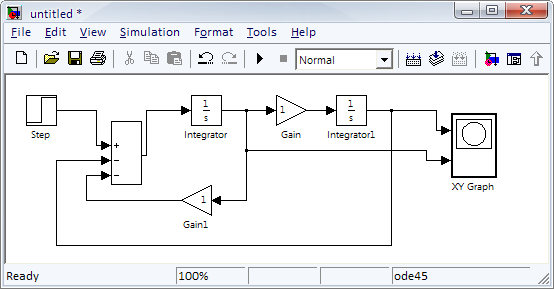
-
-
Рисунок 3.1.2 – Схема исследования в системе MatLab
-


