Файл: Лекции по теории механизмов и машин. Учебное пособие к изучению теоретических основ курса для студентов направлений 050502 Инженерная механика.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.05.2024
Просмотров: 69
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1 для плоских механизмов 2:
(2.2)
Для плоских механизмов с поступательными парами структурную формулу можно получить из (2.2), уменьшив степени подвижности каждого из слагаемых на единицу (в механизмах с поступательными парами отсутствует поворот звеньев).
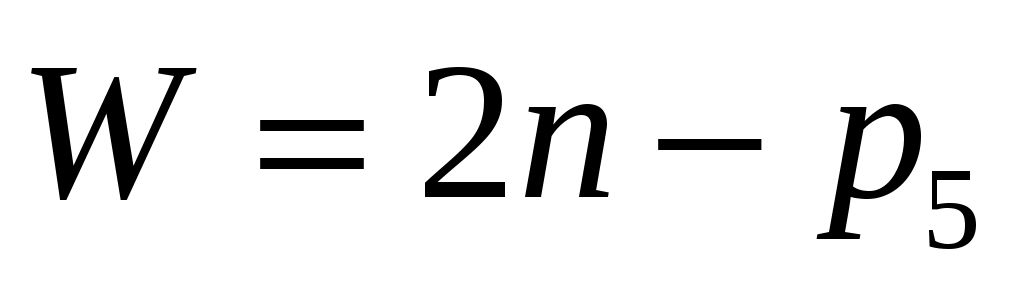(2.3)
Эта формула предложена В.В.Добровольским в 1937 г. и носит его имя.
Для примера и закрепления материала, определим степень подвижности плоского механизма, изображенного на рис.2.2.
П
рименяя формулу Чебышева, получим:
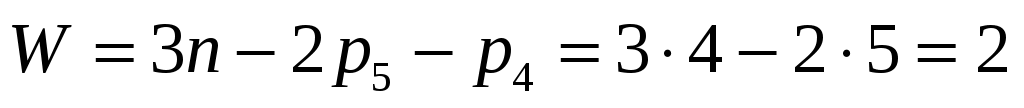
Таким образом, однозначное движение ведомых звеньев 2 и 3 можно получить, введя две обобщенные координаты (т.е. задавая движение двум начальным звеньям 1 и 4 ).
Рис.2.2
Степень подвижности плоских механизмов, показанных на рис.2.1, предлагаем определить самостоятельно.
В плоских механизмах, содержащих кинематические пары 4-го класса, для структурной классификации и кинематического исследования целесообразно заменять высшие пары низшими. 1
Замена пар является корректной, если после замены исходного механизма заменяющим степень подвижности и кинематика движения характерных точек в заменяемом и заменяющем механизмах становятся одинаковыми.
Рассмотрим механизм, изображенный на рис.2.3 сплошными линиями. Он состоит из двух подвижных звеньев АО1и ВО2 , каждое из которых входит со стойкой в кинематическую пару 5-го класса. При этом звенья контактируют между собой, образуя подвижное соединение в виде высшей пары 4-го класса. Элементами высшей пары являются дуги окружностей с центрами
и 
.
Определим степень подвижности этого механизма по формуле Чебышева:
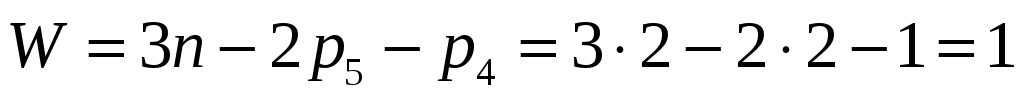
Несмотря на то, что механизм достаточно простой, кинематика движения его звеньев выглядит не вполне понятной. Причиной тому является наличие двухподвижной пары 4-го класса.
Преобразуем механизм в кинематически эквивалентный заменяющий. Учитывая, что расстояния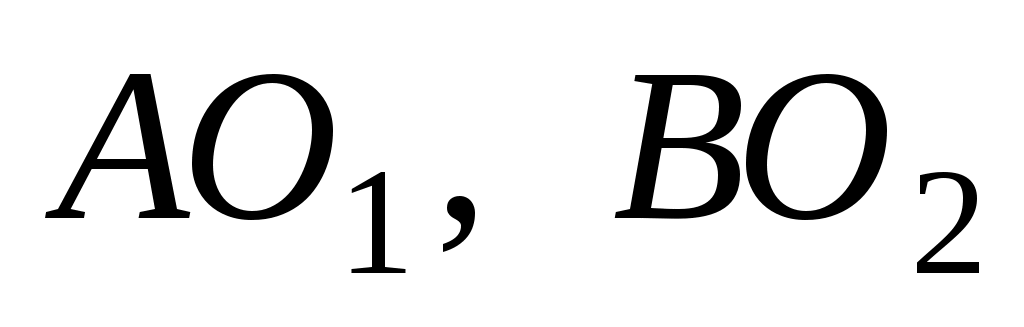
и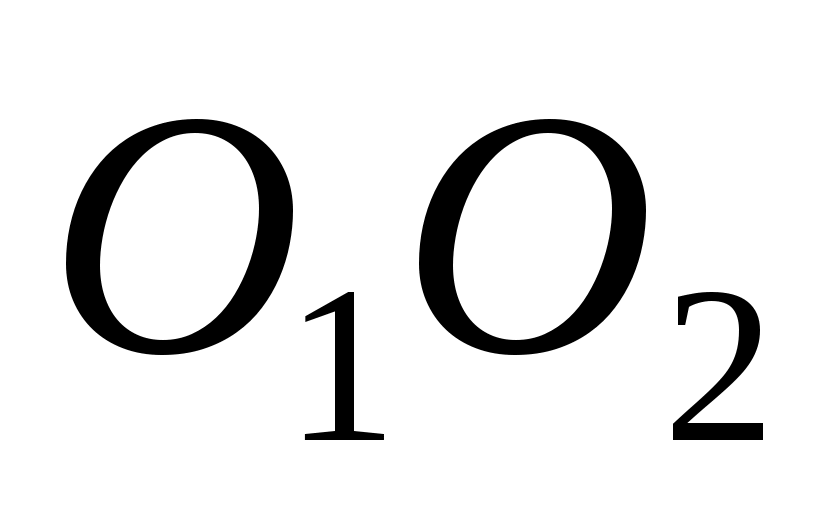 
- не изменяются, механизм
Рис.2.3 можно заменить кинематической цепью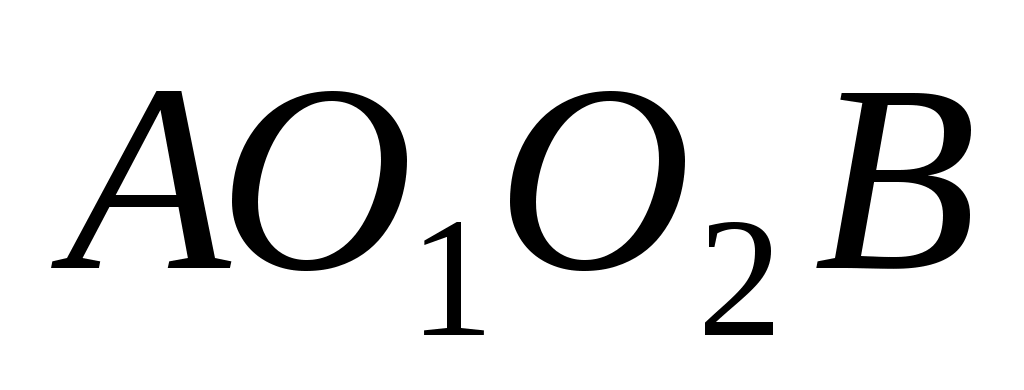
с тремя подвижными звеньями и четырьмя вращательными парами (5-го класса). Полученный механизм (на рис.2.3 показан пунктиром) кинематически подобен исходному, т.к. скорости и ускорения характерных точек А, В, 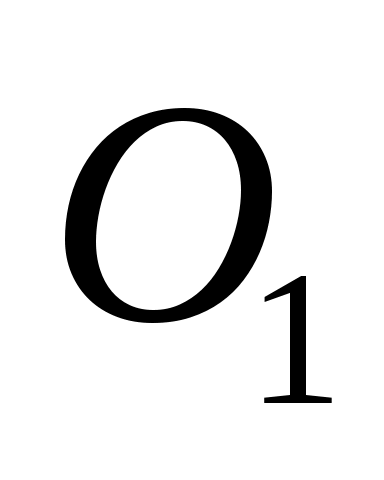и 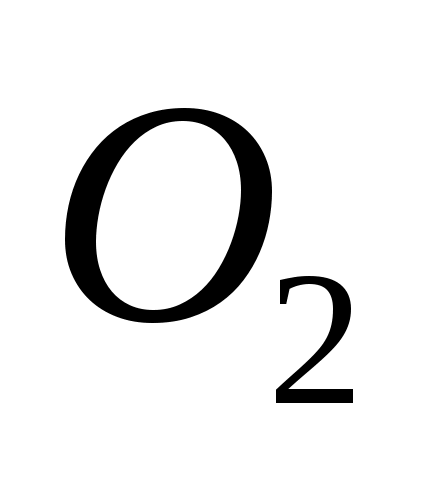в заменяемом и заменяющем механизмах являются одинаковыми. Теперь заменяющий механизм можно легко разобрать на структурные группы и определить его класс. Заметим также, что выполненные преобразования не изменили степень подвижности механизма:
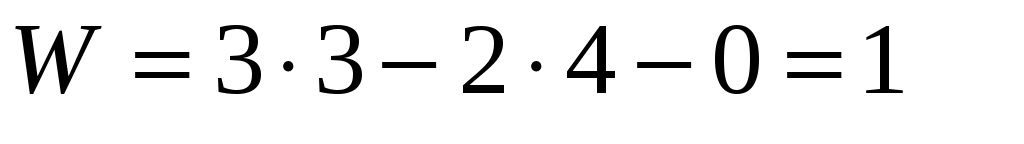
Н
а рис.2.4 приведен пример замены механизма с высшей парой заменяющим кулисным. Проверку степени подвижности исходного механизма и заменяющего предлагаем выполнить самостоятельно.
Таким образом, любой плоский механизм, содержащий кинематические пары 4-го класса может быть заменен на кинематически эквивалентный заменяющий механизм с низшими парами 5-го класса. Вид заменяющего механизма определяют по правилам, изложенным в книге [1], §10.
Рис.2.4
Следует знать, что кинематическая эквивалентность обеспечивается только для конкретных положений заменяемого и заменяющего механизмов. Поэтому такие механизмы еще называют мгновенно кинематически эквивалентными.
Как видно из приведенных примеров, полученный при замене кинематически эквивалентный механизм не является эквивалентным по структуре. Структурные изменения, происходящие в заменяющем механизме, подчиняются закону (2.4):
1 к/п 4-го класса → 2 к/п 5-го класса + 1 звено (2.4)
Как было показано в п.2.3, плоский механизм с высшими парами 4-го класса может быть преобразован в кинематически эквивалентный механизм с парами 5-го класса. Структурная формула для заменяющего механизма получит вид:
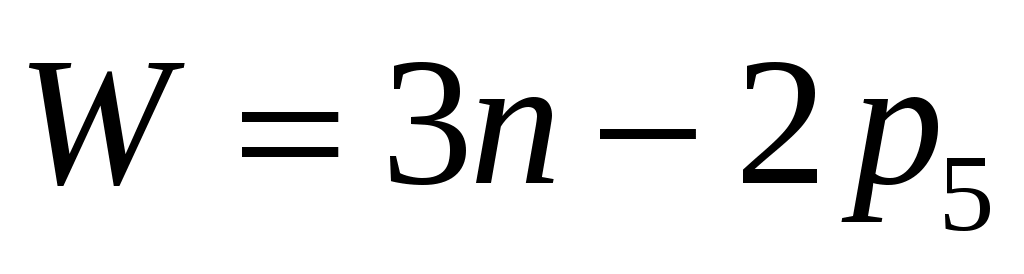(2.5)
Присутствие в механизме однотипных кинематических пар 5-го класса позволяет создать общую идеологию построения и структурной классификации всех плоских механизмов. Данная задача была выполнена Л.В.Ассуром 1 в классическом труде «Исследование плоских стержневых механизмов с низшими парами с точки зрения их структуры и классификации».2
Для понимания принципов классификации механизмов введем понятие «структурная группа».
Рассмотрим кинематическую цепь, изображенную на рис.2.5,а. Цепь состоит из звеньев 1 и 2, образующих между собой вращательную кинематическую пару. Эту кинематическую пару будем называть внутренней. Свободными концами звенья входят в кинематические пары с другими звеньями механизма (показаны пунктиром). Эти пары для рассматриваемой цепи будем считать внешними. Все кинематические пары – вращательные пары 5-го класса.
Требуется определить степень подвижности данной кинематической цепи.
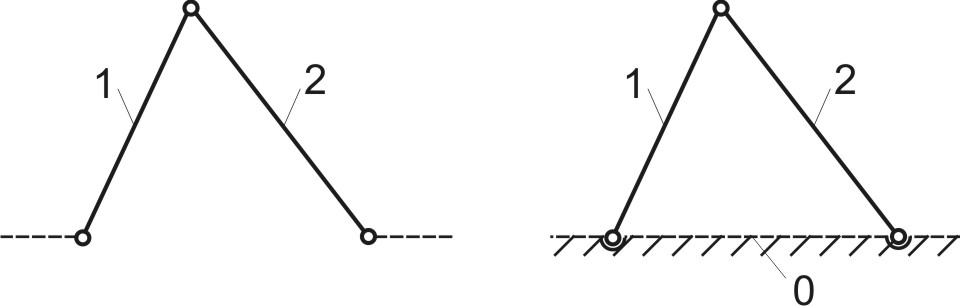
а) б)
Рис.2.5
Один из способов решения задачи заключается в мысленном присоединении рассматриваемой цепи к механизму с известной степенью подвижности (рекомендуется в [1-3]). Присоединение осуществляется элементами внешних кинематических пар. Степень подвижности вновь образованного механизма должна увеличиться на величину, равную степени подвижности исследуемой цепи звеньев.
Другим, более простым способом решения той же задачи является мысленное присоединение рассматриваемой цепи к одному, условно неподвижному звену - стойке с W=0. Как и в предыдущем случае, это присоединение осуществляется элементами внешних пар. Учитывая, что стойка имеет нулевую подвижность, степень подвижности всей цепи звеньев (включая стойку) автоматически покажет степень подвижности исследуемой кинематической цепи.
Применяя второй из описанных способов, мысленно присоединим исследуемую кинематическую цепь к стойке 0 (Рис.2.5,б) и вычислим степень подвижности полученной замкнутой цепи звеньев по формуле Чебышева:
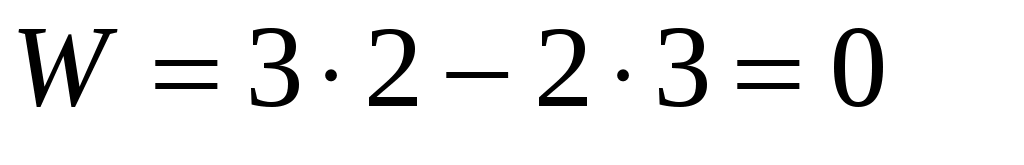
Результат свидетельствует о том, что при показанном соединении со стойкой кинематическая цепь звеньев 1 и 2, двигаться относительно стойки не может, т.е. обладает относительно нее нулевой степенью подвижности.
3
Структурной группой (группой Ассура) называют кинематическую цепь с нулевой степенью подвижности относительно звеньев, к которым она присоединена, и которая не может быть разделена на более простые кинематические цепи с нулевой степенью подвижности [1, 2].
В литературе можно встретить и другое определение, близкое по своей сути к первому.
Структурной группой называется кинематическая цепь, присоединение которой к механизму не изменяет число его степеней подвижности, причем группа не должна распадаться на более простые кинематические цепи, удовлетворяющие этому условию [2, 3].
Таким образом, при структурном анализе механизмов и выявлении структурных групп должны быть проверены два условия:
Структурной группой (группой Ассура) считают кинематическую цепь, удовлетворяющую обоим условиям одновременно.
Для иллюстрации важности второго условия приведем пример (см. Задачу ниже).
Задача.
Дано: На рис.2.6,а изображена кинематическая цепь, состоящая из 4-х звеньев.
Требуется: Выяснить, является ли данная цепь структурной группой Ассура?
а) б)
Рис.2.6
Решение.
1. Проверяем степень подвижности цепи. Для этого мысленно присоединим цепь к стойке элементами внешних кинематических пар и применим формулу Чебышева.
Получим: n = 4 , p5 = 6 и
.
Первое условие существования группы Ассура выполнено.
2. Проверяем возможность разделения исследуемой цепи на более простые цепи с W=0.
Такая возможность существует. Исходная цепь может быть разобрана на две цепи с W = 0 (Рис.2.6,б).
Ответ. Исходная кинематическая цепь не является структурной группой.
Для выявления и классификации структурных групп выясним вопрос о вероятных сочетаниях числа звеньев и числа кинематических пар в различных структурных группах. Для этого используем формулу Чебышева для механизмов с парами 5-го класса, подставив в нее условие
W=0.
Получим: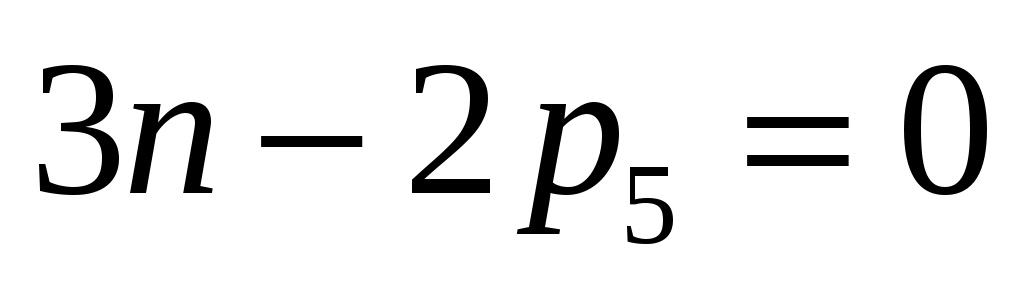
(2.6)
Отсюда следует: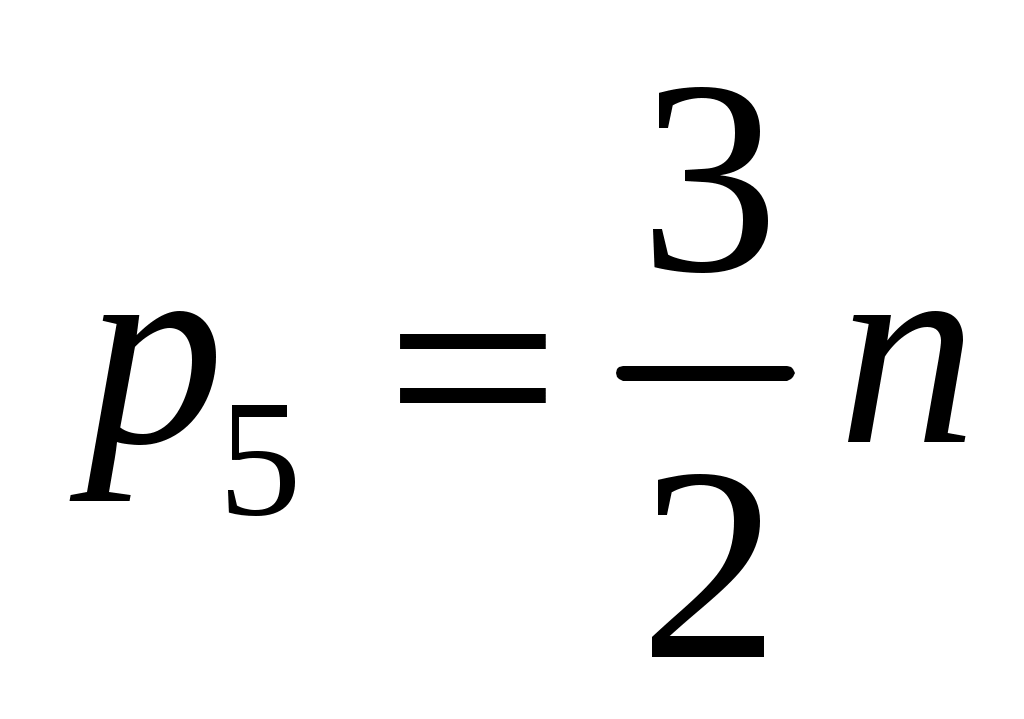
(2.7)
и возможные сочетания
и 
из условия, что это целые числа.
Таблица 2.1
Из таблицы видно, что самая простая структурная группа имеет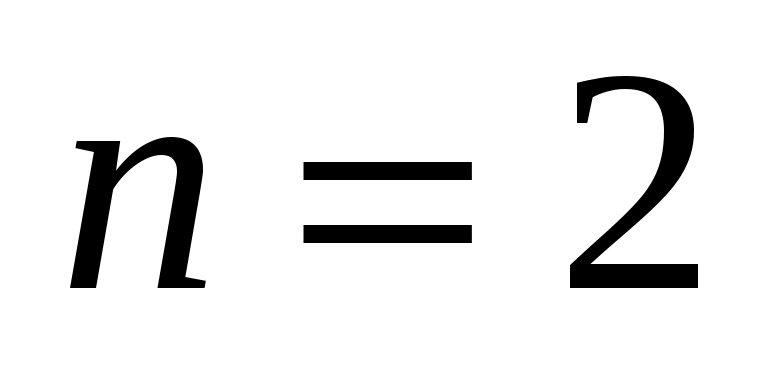
и 
. Эту структурную группу называют «двухповодковой группой» или «диадой». В зависимости от сочетания вращательных и поступательных пар 5-го класса в кинематической цепи, диады делятся на виды (модификации).
Таблица 2.2
Виды двухповодковых структурных групп (диад)
Диада 6-го вида, с тремя поступательными кинематическими парами, в таблице 2.2 намерено перечеркнута. Это означает, что она не существует. В этом можно убедиться, присоединив данную кинематическую цепь элементами внешних пар к стойке и применив структурную формулу Добровольского для механизмов с поступательными парами:
(2.2)Для плоских механизмов с поступательными парами структурную формулу можно получить из (2.2), уменьшив степени подвижности каждого из слагаемых на единицу (в механизмах с поступательными парами отсутствует поворот звеньев).
(2.3)Эта формула предложена В.В.Добровольским в 1937 г. и носит его имя.
Для примера и закрепления материала, определим степень подвижности плоского механизма, изображенного на рис.2.2.
П
рименяя формулу Чебышева, получим: Таким образом, однозначное движение ведомых звеньев 2 и 3 можно получить, введя две обобщенные координаты (т.е. задавая движение двум начальным звеньям 1 и 4 ).
Рис.2.2
Степень подвижности плоских механизмов, показанных на рис.2.1, предлагаем определить самостоятельно.
-
Замена высших кинематических пар низшими.
В плоских механизмах, содержащих кинематические пары 4-го класса, для структурной классификации и кинематического исследования целесообразно заменять высшие пары низшими. 1
Замена пар является корректной, если после замены исходного механизма заменяющим степень подвижности и кинематика движения характерных точек в заменяемом и заменяющем механизмах становятся одинаковыми.
Рассмотрим механизм, изображенный на рис.2.3 сплошными линиями. Он состоит из двух подвижных звеньев АО1и ВО2 , каждое из которых входит со стойкой в кинематическую пару 5-го класса. При этом звенья контактируют между собой, образуя подвижное соединение в виде высшей пары 4-го класса. Элементами высшей пары являются дуги окружностей с центрами
и . Определим степень подвижности этого механизма по формуле Чебышева:
Несмотря на то, что механизм достаточно простой, кинематика движения его звеньев выглядит не вполне понятной. Причиной тому является наличие двухподвижной пары 4-го класса.
Преобразуем механизм в кинематически эквивалентный заменяющий. Учитывая, что расстояния
и - не изменяются, механизмРис.2.3 можно заменить кинематической цепью
с тремя подвижными звеньями и четырьмя вращательными парами (5-го класса). Полученный механизм (на рис.2.3 показан пунктиром) кинематически подобен исходному, т.к. скорости и ускорения характерных точек А, В, и в заменяемом и заменяющем механизмах являются одинаковыми. Теперь заменяющий механизм можно легко разобрать на структурные группы и определить его класс. Заметим также, что выполненные преобразования не изменили степень подвижности механизма: Н
а рис.2.4 приведен пример замены механизма с высшей парой заменяющим кулисным. Проверку степени подвижности исходного механизма и заменяющего предлагаем выполнить самостоятельно. Таким образом, любой плоский механизм, содержащий кинематические пары 4-го класса может быть заменен на кинематически эквивалентный заменяющий механизм с низшими парами 5-го класса. Вид заменяющего механизма определяют по правилам, изложенным в книге [1], §10.
Рис.2.4
Следует знать, что кинематическая эквивалентность обеспечивается только для конкретных положений заменяемого и заменяющего механизмов. Поэтому такие механизмы еще называют мгновенно кинематически эквивалентными.
Как видно из приведенных примеров, полученный при замене кинематически эквивалентный механизм не является эквивалентным по структуре. Структурные изменения, происходящие в заменяющем механизме, подчиняются закону (2.4):
1 к/п 4-го класса → 2 к/п 5-го класса + 1 звено (2.4)
-
Структурные группы Л.В.Ассура. Классификация структурных групп
Как было показано в п.2.3, плоский механизм с высшими парами 4-го класса может быть преобразован в кинематически эквивалентный механизм с парами 5-го класса. Структурная формула для заменяющего механизма получит вид:
(2.5)Присутствие в механизме однотипных кинематических пар 5-го класса позволяет создать общую идеологию построения и структурной классификации всех плоских механизмов. Данная задача была выполнена Л.В.Ассуром 1 в классическом труде «Исследование плоских стержневых механизмов с низшими парами с точки зрения их структуры и классификации».2
Для понимания принципов классификации механизмов введем понятие «структурная группа».
Рассмотрим кинематическую цепь, изображенную на рис.2.5,а. Цепь состоит из звеньев 1 и 2, образующих между собой вращательную кинематическую пару. Эту кинематическую пару будем называть внутренней. Свободными концами звенья входят в кинематические пары с другими звеньями механизма (показаны пунктиром). Эти пары для рассматриваемой цепи будем считать внешними. Все кинематические пары – вращательные пары 5-го класса.
Требуется определить степень подвижности данной кинематической цепи.
а) б)
Рис.2.5
Один из способов решения задачи заключается в мысленном присоединении рассматриваемой цепи к механизму с известной степенью подвижности (рекомендуется в [1-3]). Присоединение осуществляется элементами внешних кинематических пар. Степень подвижности вновь образованного механизма должна увеличиться на величину, равную степени подвижности исследуемой цепи звеньев.
Другим, более простым способом решения той же задачи является мысленное присоединение рассматриваемой цепи к одному, условно неподвижному звену - стойке с W=0. Как и в предыдущем случае, это присоединение осуществляется элементами внешних пар. Учитывая, что стойка имеет нулевую подвижность, степень подвижности всей цепи звеньев (включая стойку) автоматически покажет степень подвижности исследуемой кинематической цепи.
Применяя второй из описанных способов, мысленно присоединим исследуемую кинематическую цепь к стойке 0 (Рис.2.5,б) и вычислим степень подвижности полученной замкнутой цепи звеньев по формуле Чебышева:
Результат свидетельствует о том, что при показанном соединении со стойкой кинематическая цепь звеньев 1 и 2, двигаться относительно стойки не может, т.е. обладает относительно нее нулевой степенью подвижности.
3
Структурной группой (группой Ассура) называют кинематическую цепь с нулевой степенью подвижности относительно звеньев, к которым она присоединена, и которая не может быть разделена на более простые кинематические цепи с нулевой степенью подвижности [1, 2].
В литературе можно встретить и другое определение, близкое по своей сути к первому.
Структурной группой называется кинематическая цепь, присоединение которой к механизму не изменяет число его степеней подвижности, причем группа не должна распадаться на более простые кинематические цепи, удовлетворяющие этому условию [2, 3].
Таким образом, при структурном анализе механизмов и выявлении структурных групп должны быть проверены два условия:
-
Степень подвижности выделенной кинематической цепи (предположительно – структурной группы) после присоединения к стойке элементами внешних пар должна быть W=0. -
Выделенная кинематическая цепь (предположительно – структурная группа) не должна распадаться на более простые цепи с W=0.
Структурной группой (группой Ассура) считают кинематическую цепь, удовлетворяющую обоим условиям одновременно.
Для иллюстрации важности второго условия приведем пример (см. Задачу ниже).
Задача.
Дано: На рис.2.6,а изображена кинематическая цепь, состоящая из 4-х звеньев.
Требуется: Выяснить, является ли данная цепь структурной группой Ассура?
а) б)
Рис.2.6
Решение.
1. Проверяем степень подвижности цепи. Для этого мысленно присоединим цепь к стойке элементами внешних кинематических пар и применим формулу Чебышева.
Получим: n = 4 , p5 = 6 и
. Первое условие существования группы Ассура выполнено.
2. Проверяем возможность разделения исследуемой цепи на более простые цепи с W=0.
Такая возможность существует. Исходная цепь может быть разобрана на две цепи с W = 0 (Рис.2.6,б).
Ответ. Исходная кинематическая цепь не является структурной группой.
Для выявления и классификации структурных групп выясним вопрос о вероятных сочетаниях числа звеньев и числа кинематических пар в различных структурных группах. Для этого используем формулу Чебышева для механизмов с парами 5-го класса, подставив в нее условие
W=0.
Получим:
(2.6)Отсюда следует:
(2.7) и возможные сочетания
и из условия, что это целые числа.Таблица 2.1
| | 2 | 4 | 6 | ……. |
| | 3 | 6 | 9 | …….. |
Из таблицы видно, что самая простая структурная группа имеет
и . Эту структурную группу называют «двухповодковой группой» или «диадой». В зависимости от сочетания вращательных и поступательных пар 5-го класса в кинематической цепи, диады делятся на виды (модификации).Таблица 2.2
Виды двухповодковых структурных групп (диад)
| 1 | 2 | 3 | 4 | 5 | 6 |
 |  | | |  | |
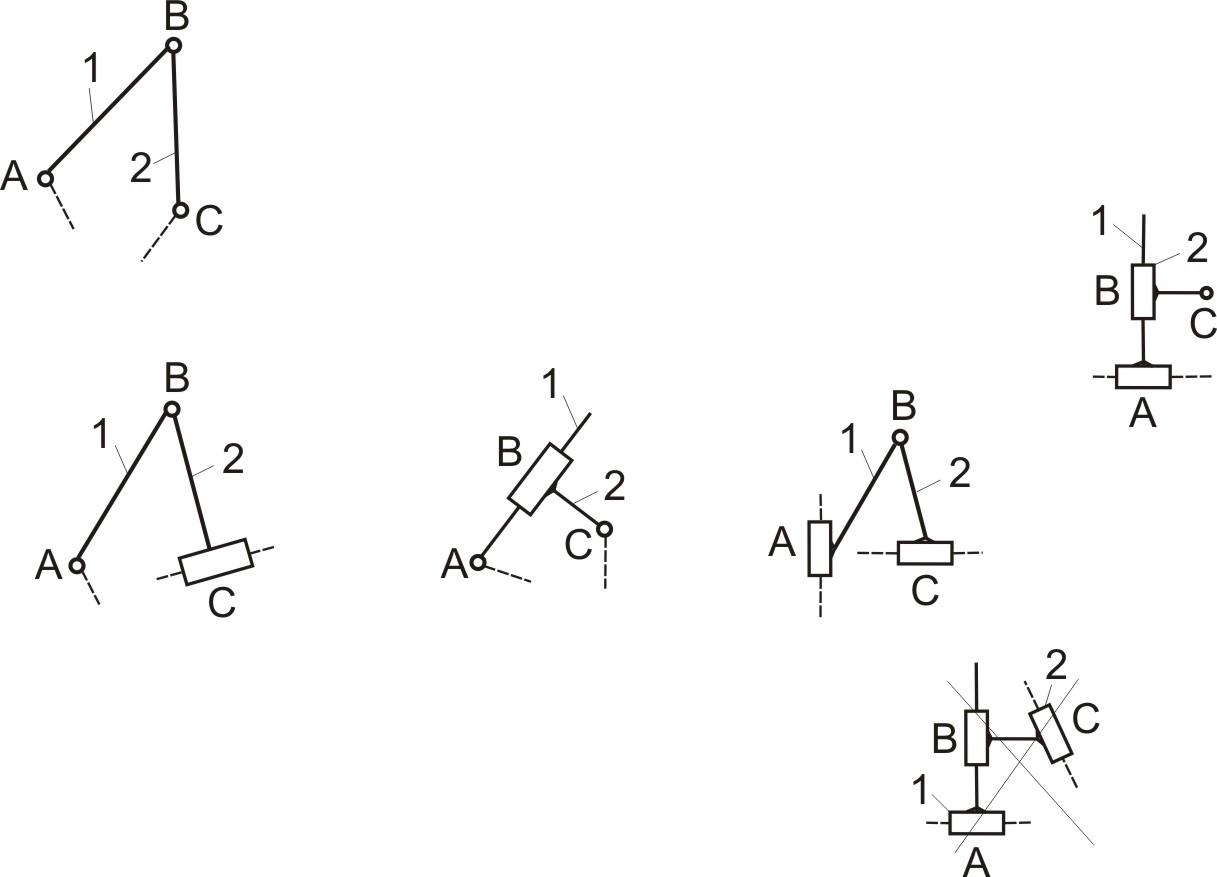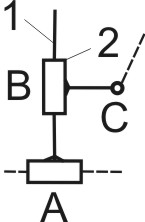Диада 6-го вида, с тремя поступательными кинематическими парами, в таблице 2.2 намерено перечеркнута. Это означает, что она не существует. В этом можно убедиться, присоединив данную кинематическую цепь элементами внешних пар к стойке и применив структурную формулу Добровольского для механизмов с поступательными парами:
