Файл: Методические указания по выполнению практических заданий по дисциплине математика ( О. 7) для специальности 23. 05. 05 Системы обеспечения движения поездов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.10.2024
Просмотров: 44
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, 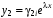 ,
, 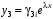 :
: 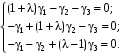
Характеристическое уравнение: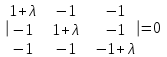 .
.
Корни характеристического уравнения: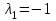 ,
, 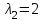 ,
, 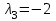 .
.
Собственный вектор для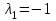 :
: 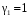 ,
, 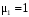 ,
, 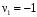 ,
,
Собственный вектор для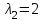 :
: 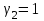 ,
, 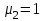 ,
, 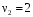 ,
,
Собственный вектор для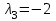 :
: 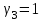 ,
, 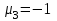 ,
, 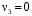 .
.
Фундаментальная система решений: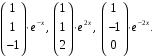
Общее решение системы: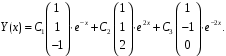
1. Запишите систему уравнений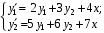 в матричной форме.
в матричной форме.
Ответ: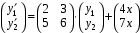 .
.
2. Докажите, что функции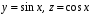 являются решением системы уравнений
являются решением системы уравнений 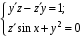 при начальных условиях
при начальных условиях 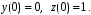
3. Найдите общее решение системы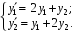
Ответ: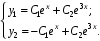
4. Найдите общее решение системы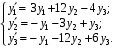
Ответ: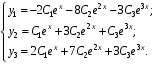
5. Найдите частное решение системы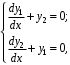
если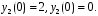
Ответ: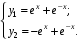
6. Найдите частное решение системы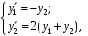 если
если 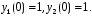
Ответ: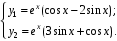
7. Найдите частное решение системы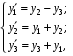
если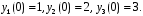
Ответ: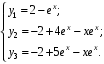
Пример. Найти изображение функции ƒ(t) = еаt, аR.
F(p) =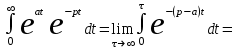
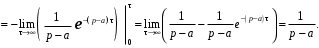 Пример. Найти изображение функции ƒ(t) = sh(ωt) =
Пример. Найти изображение функции ƒ(t) = sh(ωt) = 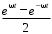 , R.
, R.
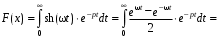
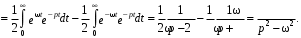
Пример. Найти изображение функции ƒ(t) = sin(ωt), R.
Формула Эйлера: еi = cos + isin,е–i = cos – isin.
Комплексное представление функции sin(ωt):
.
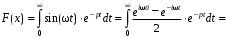
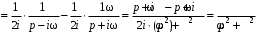 .
.
Пример. Найти изображение функции ƒ(t) = t.
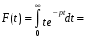 формула интегрирования по частям
формула интегрирования по частям 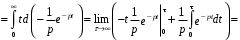
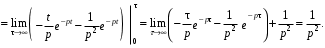
Пример. Найти изображение функции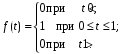
f(t) – единичный импульс (рис. 5).
Представление единичного импульса в виде разности двух функций (рис. 2, 6): f(t) = 1(t) – 1(t – 1).
Изображение функции Хэвисайда: 1(t)  .
.
Теорема запаздывания для функции Хэвисайда: 1(t – 1) 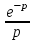 ;
;
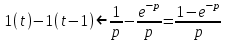 .
.
Пример. Доказать теорему дифференцирования оригиналов:

 , если f(t) F(p).
, если f(t) F(p).
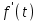
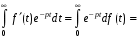 формула интегрирования по частям
формула интегрирования по частям 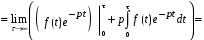
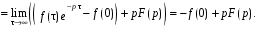
Пример. Найти оригинал функции F(p) =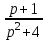 .
.
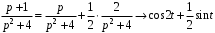 – пункты 3, 4 таблицы 1.
– пункты 3, 4 таблицы 1.
Пример
. Найти оригинал изображения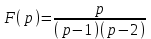 .
.
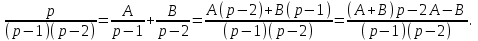
Числители дробей одинаковы: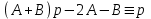 .
.
Система для нахождения значений неопределенных коэффициентов А, В: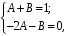
Решение системы: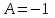 ,
, 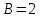 .
.
Разложение F(p) на элементарные дроби: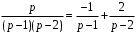 .
.
Искомый оригинал (табл. 1):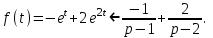
Пример. Найти изображение ступенчатой функции, заданной на промежутке [0; +), четыре ступени которой представлены на рисунке 7.
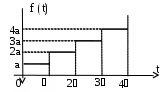
Рис. 7
Аналитическое выражение функции f(t):
Изображение для f(t):
Слагаемые в скобках образуют убывающую бесконечную геометрическую прогрессию с знаменателем .
.
Сумма прогрессии:
Пример. Найти изображение импульсной дельта-функции Дирака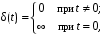 если
если 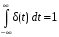 .
.
Рассмотрим прямоугольный импульс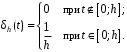
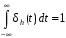 при любом значении h.
при любом значении h.
Представление функции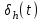 в виде разности двух функций Хэвисайда:
в виде разности двух функций Хэвисайда: 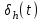 =
= 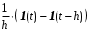 .
.
Изображение прямоугольного импульса: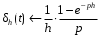 .
.
Изображение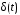
равно пределу при h 0 изображения :
:
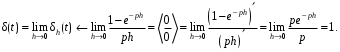
Пример. Найти решение уравнения y''–2y'– 8y = et, удовлетворяющее начальным условиям y(0) = 0,y'(0) =0.
Изображение правой части уравнения: et ←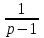 ;
;
изображение искомого решения: y(t) ← Y(p);
изображения производных: y'(t) pY(p),y''(t) p2Y(p);
операторное уравнение: p2Y(p) – 2pY(p) – 8Y(p) =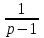 .
.
Решение операторного уравнения: Y(p) =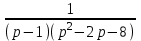 ;
;
Разложение фнуции Y(p) на сумму элементарных дробей:
 .
.
Частное решение д.у.: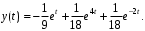
Пример. Найти общее решение уравнения y'– 2y = et.
Назначим начальное условие: y(0) = с.
Изображение правой части уравнения: et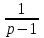 ;
;
изображение искомого решения: y(t) Y(p);
изображения производной: y'(t) pY(p) – с;
операторное уравнение: pY(p) – с– 2Y(p) =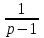 .
.
Решение операторного уравнения: Y(p) = ;
;
разложение Y(p) на сумму элементарных дробей:

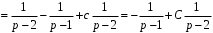 , где С = с + 1.
, где С = с + 1.
Общее решение д.у.: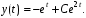
Пример. Найти частное решение системы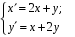 при начальных условиях
при начальных условиях 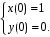
Частное решение системы:
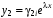 ,
, 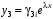 :
: 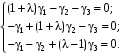
Характеристическое уравнение:
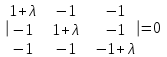 .
.Корни характеристического уравнения:
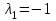 ,
, 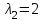 ,
, 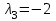 .
.Собственный вектор для
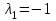 :
: 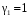 ,
, 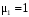 ,
, 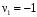 ,
,Собственный вектор для
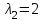 :
: 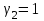 ,
, 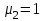 ,
, 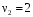 ,
,Собственный вектор для
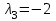 :
: 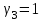 ,
, 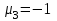 ,
, 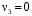 .
.Фундаментальная система решений:
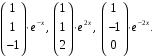
Общее решение системы:
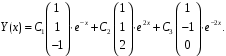
ЗАДАЧИ ДЛЯ РЕШЕНИЯ
1. Запишите систему уравнений
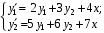 в матричной форме.
в матричной форме. Ответ:
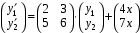 .
.2. Докажите, что функции
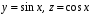 являются решением системы уравнений
являются решением системы уравнений 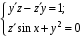 при начальных условиях
при начальных условиях 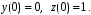
3. Найдите общее решение системы
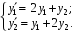
Ответ:
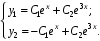
4. Найдите общее решение системы
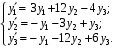
Ответ:
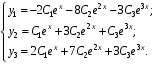
5. Найдите частное решение системы
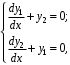
если
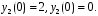
Ответ:
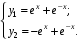
6. Найдите частное решение системы
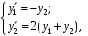 если
если 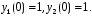
Ответ:
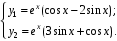
7. Найдите частное решение системы
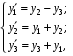
если
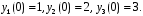
Ответ:
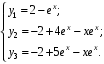
Тема 9
Оригиналы и изображения
Пример. Найти изображение функции ƒ(t) = еаt, аR.
F(p) =
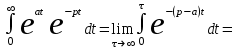
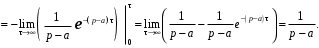 Пример. Найти изображение функции ƒ(t) = sh(ωt) =
Пример. Найти изображение функции ƒ(t) = sh(ωt) = 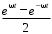 , R.
, R.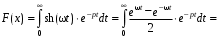
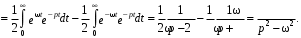
Пример. Найти изображение функции ƒ(t) = sin(ωt), R.
Формула Эйлера: еi = cos + isin,е–i = cos – isin.
Комплексное представление функции sin(ωt):

.
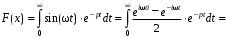
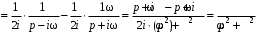 .
.Пример. Найти изображение функции ƒ(t) = t.
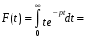 формула интегрирования по частям
формула интегрирования по частям 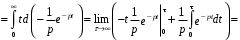
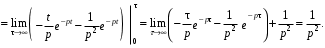
Теоремы операционного исчисления
Пример. Найти изображение функции
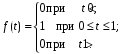
f(t) – единичный импульс (рис. 5).
Представление единичного импульса в виде разности двух функций (рис. 2, 6): f(t) = 1(t) – 1(t – 1).
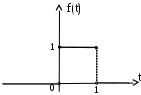 Рис. 5 | 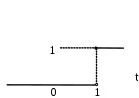 1(t – 1) Рис. 6 |
Изображение функции Хэвисайда: 1(t)
Теорема запаздывания для функции Хэвисайда: 1(t – 1)
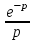 ;
; 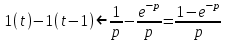 .
.Пример. Доказать теорему дифференцирования оригиналов:
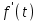
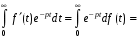 формула интегрирования по частям
формула интегрирования по частям 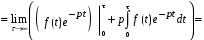
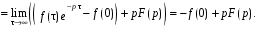
Тема 10
Изображения основных функций
Пример. Найти оригинал функции F(p) =
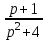 .
.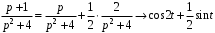 – пункты 3, 4 таблицы 1.
– пункты 3, 4 таблицы 1.Пример
. Найти оригинал изображения
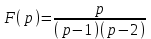 .
.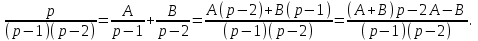
Числители дробей одинаковы:
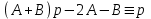 .
. Система для нахождения значений неопределенных коэффициентов А, В:
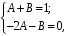
Решение системы:
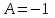 ,
, 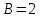 .
. Разложение F(p) на элементарные дроби:
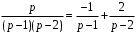 .
.Искомый оригинал (табл. 1):
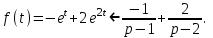
Пример. Найти изображение ступенчатой функции, заданной на промежутке [0; +), четыре ступени которой представлены на рисунке 7.

Рис. 7
Аналитическое выражение функции f(t):
Изображение для f(t):

Слагаемые в скобках образуют убывающую бесконечную геометрическую прогрессию с знаменателем
Сумма прогрессии:

Пример. Найти изображение импульсной дельта-функции Дирака
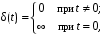 если
если 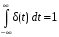 .
. Рассмотрим прямоугольный импульс
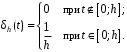
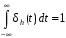 при любом значении h.
при любом значении h.Представление функции
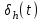 в виде разности двух функций Хэвисайда:
в виде разности двух функций Хэвисайда: 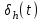 =
= 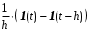 .
.Изображение прямоугольного импульса:
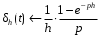 .
.Изображение
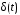
равно пределу при h 0 изображения
 :
: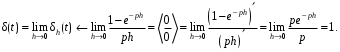
Тема 11
Решение дифференциальных уравнений
Пример. Найти решение уравнения y''–2y'– 8y = et, удовлетворяющее начальным условиям y(0) = 0,y'(0) =0.
Изображение правой части уравнения: et ←
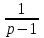 ;
;изображение искомого решения: y(t) ← Y(p);
изображения производных: y'(t) pY(p),y''(t) p2Y(p);
операторное уравнение: p2Y(p) – 2pY(p) – 8Y(p) =
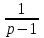 .
.Решение операторного уравнения: Y(p) =
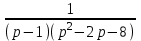 ;
;Разложение фнуции Y(p) на сумму элементарных дробей:
 .
.Частное решение д.у.:
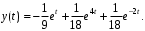
Пример. Найти общее решение уравнения y'– 2y = et.
Назначим начальное условие: y(0) = с.
Изображение правой части уравнения: et
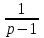 ;
;изображение искомого решения: y(t) Y(p);
изображения производной: y'(t) pY(p) – с;
операторное уравнение: pY(p) – с– 2Y(p) =
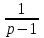 .
.Решение операторного уравнения: Y(p) =
 ;
;разложение Y(p) на сумму элементарных дробей:

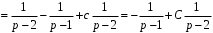 , где С = с + 1.
, где С = с + 1.Общее решение д.у.:
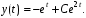
Решение систем уравнений
Пример. Найти частное решение системы
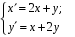 при начальных условиях
при начальных условиях 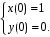
Частное решение системы:
