Файл: Методические указания по выполнению практических заданий по дисциплине математика ( О. 7) для специальности 23. 05. 05 Системы обеспечения движения поездов.docx

Однородное уравнение:

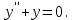
Характеристическое уравнение: l² + 1 = 0.

Корни характеристического уравнения: , .

Фундаментальная система решений: , .

Общее решение однородного уравнения:

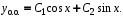
Правая часть дифференциального уравнения: .

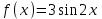Число 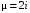не совпадает с корнями характеристического уравнения:r = 0.

Вид частного решения:

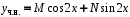(строка 7 таблицы 4.3).

Производные частного решения: , .

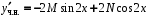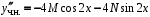После подстановки , в уравнение :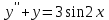



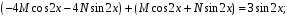
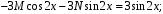M = 0, N = –1.

Частное решение д.у.:

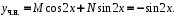
Общее решение д.у.:

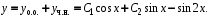
Пример. Найти общее решение уравнения .

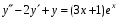Однородное уравнение: .

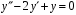Характеристическое уравнение: l² – 2l + 1 = 0.

Корни характеристического уравнения: , .;

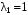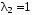Фундаментальная система решений: .

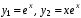Общее решение однородного уравнения: .

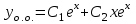Правая часть дифференциального уравнения:

---

.

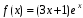
Два совпадения числа 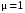с корнями характеристического уравнения: r = 2.

Вид частного решения:

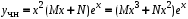(строка 3 таблицы 13.3).

Подстановка , в уравнение 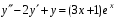приводит к равенству 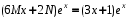, откуда , .

Частное решение: .

Общее решение: .

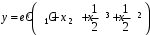Пример. Найти решение уравнения ,

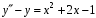удовлетворяющее начальным условиям , .

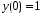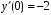Однородное уравнение: .

Характеристическое уравнение: l² – 1 = 0.

Корни характеристического уравнения: , .

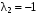Фундаментальная система решений: .

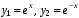Общее решение однородного уравнения: .

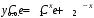Правая часть дифференциального уравнения: .

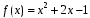Число m = 0 не совпадает с корнями характеристического уравнения:r = 0.

Вид частного решения: 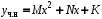(строка 6 таблицы 4.3).

Подстановка ,

---

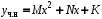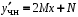
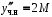, в уравнение .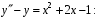

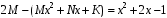Приравнивание коэффициентов при одинаковых степенях х в левой и правой частях равенства приводит к системе

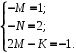
Неопределенные коэффициенты: M = –1, N = –2, K = –1.

Частное решение: .

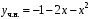Общее решение: .

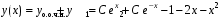Производная общего решения: .

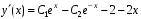При , :

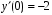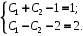
Значения произвольных постоянных: С₁ = 3, С₂ = –1.

Решения задачи Коши: .

Пример. Найти частное решение уравнения .

, .

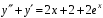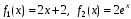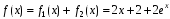Частное решение для f₁(x): .

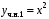Частное решение для f₂(x): .

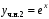Частное решение для f(x): .

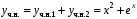Пример. Найти частное решение уравнения .

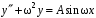Однородное уравнение: .

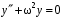Характеристическое уравнение: l² + w² = 0.

Корни характеристического уравнения: , .

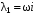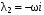Правая часть дифференциального уравнения: .

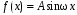Число m = wi совпадает с корнем характеристического уравнения.

Вид частного решения (строка 7 табл. 4.3):

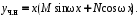
Производные частного решения:

---

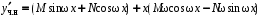
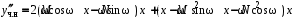
. Подстановка 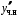в уравнение :

.

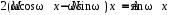Значения неопределенных коэффициентов:

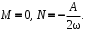
Частное решение: .

---

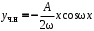ЗАДАЧИ ДЛЯ РЕШЕНИЯ

1. Найдите общее решение уравнения .

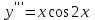Ответ: .
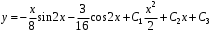2. Найдите частное решение уравнения 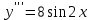при начальных условиях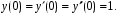

Ответ: .
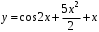3. Найдите общее решение уравнения .

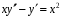Ответ:
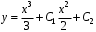
4. Найдите частное решение уравнения 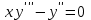при начальных условиях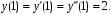

Ответ: .
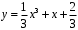5. Найдите общее решение уравнения .

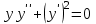Ответ:
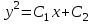
6. Найдите частное решение уравнения 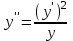при начальных условиях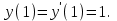

Ответ: .
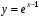7. Найдите общее решение уравнения .

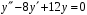Ответ: .
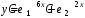8. Найдите общее решение уравнения .

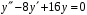Ответ: .
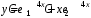9. Найдите общее решение уравнения .

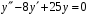Ответ: .
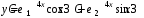10. Найдите общее решение уравнения .

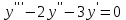Ответ: .
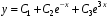11. Найдите общее решение уравнения y¢¢¢ + 3y¢¢ + 3y¢ + y = 0.

Ответ: .

---
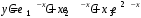