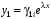Файл: Методические указания по выполнению практических заданий по дисциплине математика ( О. 7) для специальности 23. 05. 05 Системы обеспечения движения поездов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.10.2024
Просмотров: 42
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
12. Найдите общее решение уравнения 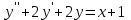 .
.
Ответ: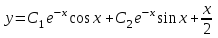 .
.
13. Найдите общее решение уравнения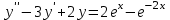 .
.
Ответ: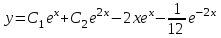 .
.
14. Найдите общее решение уравнения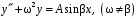 .
.
Ответ: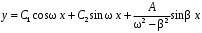 .
.
15. Найдите решение уравнения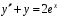 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 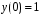 ,
,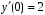 .
.
Ответ: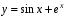 .
.
16. Найдите решение уравнения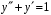 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 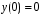 ,
,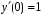 .
.
Ответ: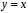 .
.
17. Найдите решение уравнения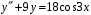 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 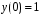 ,
,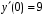 .
.
Ответ: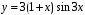 .
.
Пример.Преобразовать систему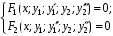
к системе уравнений первого порядка.
Эквивалентная система д.у. первого порядка: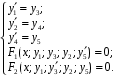
Пример. Представить каноническую систему д.у. третьего порядка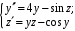 эквивалентной нормальной системой.
эквивалентной нормальной системой.
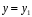 ,
, 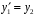 ,
, 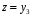 :
: 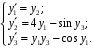
Пример. Представить дифференциальное уравнение третьего порядка
эквивалентной нормальной системой.
Эквивалентная система д.у. первого порядка: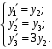
Пример. Найти общее решение системы д.у.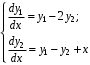 методом исключения неизвестных, преобразовав систему в дифференциальное уравнение второго порядка.
методом исключения неизвестных, преобразовав систему в дифференциальное уравнение второго порядка.
Производная первого уравнения системы: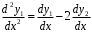 .
.
Замена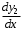 в уравнении
в уравнении 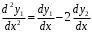 :
: 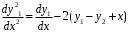 .
.
Замена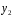 на
на 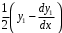 :
: 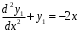 .
.
Общее решение д.у.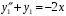 :
: 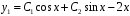 .
.
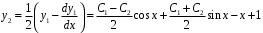 .
.
Общее решение системы д.у.: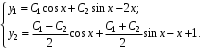
Пример. Записать систему уравнений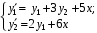 в матричной форме.
в матричной форме.
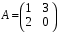 ,
, 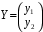 ,
, 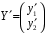 ,
, 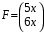 .
.
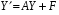 или
или 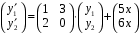 .
.
Пример. Установить линейную зависимость или независимость вектор-функций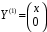 и
и 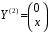 .
.
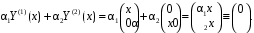
Линейная комбинация тождественно равна нулю только в случае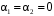 . Вектор-функции линейно независимы.
. Вектор-функции линейно независимы.
Пример. Доказать, что если вектор-функции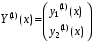 и
и 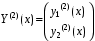 линейно зависимы, то определитель Вронского
линейно зависимы, то определитель Вронского 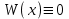
.
Пусть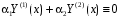 и один из коэффициентов отличен от нуля, например,
и один из коэффициентов отличен от нуля, например, 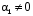 .
.
Тогда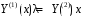 и
и 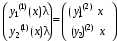 , где
, где 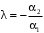 .
. 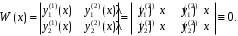
Пример. Установить линейную зависимость или независимость вектор-функций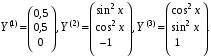
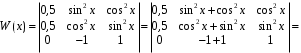
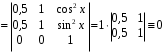
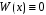 при любых значениях х. Функции линейно зависимы.
при любых значениях х. Функции линейно зависимы.
Действительно, существуют отличные от нуля коэффициенты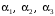 , при которых линейная комбинация
, при которых линейная комбинация 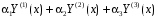 тождественно равна нулю, например,
тождественно равна нулю, например,
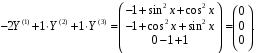
Пример. Найти общее решение системы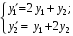 двумя способами.
двумя способами.
I способ. Матрица системы: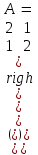 .
.
Характеристическое уравнение: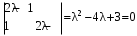 .
.
Корни характеристического уравнения: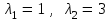 .
.
Фундаментальная система решений:
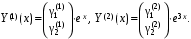
Уравнение для нахождения собственных векторов: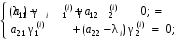
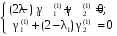 при
при 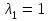 :
: 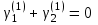 .
.
Собственный вектор для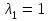 :
: 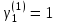 ,
, 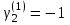
.
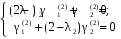 при
при 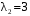 :
: 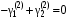 .
.
Собственный вектор для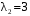 :
: 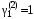 ,
, 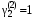 .
.
Общее решение системы: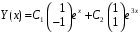
или в скалярной форме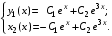
II способ. Корни характеристического уравнения: .
.
Вид общего решения (таблица 13.2):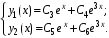
Подстановка решения в первое уравнение системы:
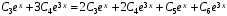 .
.
Коэффициенты при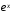 :
: 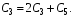
Коэффициенты при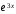 :
: 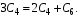
Общее решение системы при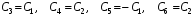 :
:
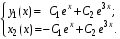
Пример. Двумя способами найти частное решение системы уравнений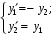 при начальных условиях
при начальных условиях 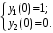 .
.
I способ. Матрица системы: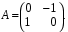
Характеристическое уравнение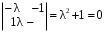 .
.
Корни характеристического уравнения: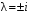 .
.
Фундаментальная система решений:
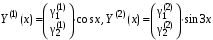 .
.
Уравнение для нахождения собственных векторов: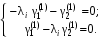
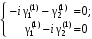 при
при 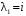 :
: 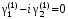 .
.
Собственный вектор для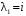 :
: 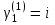
,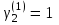 .
.
Комплексное решение системы:
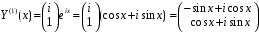 .
.
Вещественная и мнимая части комплексного решения:
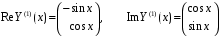 .
.
Общее решение системы: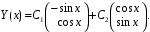
или в скалярной форме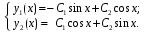
Начальные условия: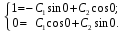
Значения произвольных постоянных: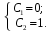
Частное решение, удовлетворяющее начальным условиям: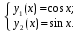
II способ. Корни характеристического уравнения: .
.
Вид общего решения (таблица 13.2):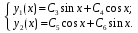
Подстановка решения в первое уравнение системы: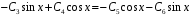 .
.
Коэффициенты при sinх:
Коэффициенты при cosх: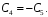
Общее решение системы при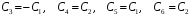 :
:
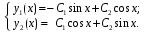
Частное решение, удовлетворяющее начальным условиям: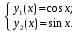
Пример. Найти общее решение системы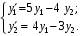
I. Матрица системы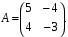
Характеристическое уравнение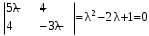 .
.
Корни характеристического уравнения: .
.
Фундаментальная система частных решений: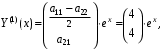
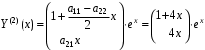 .
.
Общее решение системы: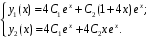
Пример. Найти общее решение системы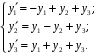
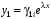
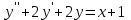 .
.Ответ:
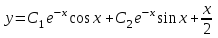 .
.13. Найдите общее решение уравнения
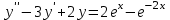 .
.Ответ:
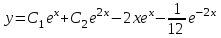 .
.14. Найдите общее решение уравнения
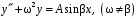 .
.Ответ:
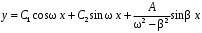 .
.15. Найдите решение уравнения
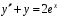 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 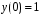 ,
,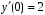 .
.Ответ:
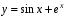 .
.16. Найдите решение уравнения
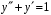 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 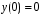 ,
,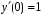 .
.Ответ:
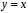 .
.17. Найдите решение уравнения
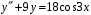 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 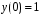 ,
,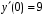 .
.Ответ:
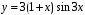 .
.Тема 8
СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Пример.Преобразовать систему
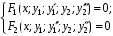
к системе уравнений первого порядка.
Эквивалентная система д.у. первого порядка:
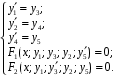
Пример. Представить каноническую систему д.у. третьего порядка
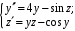 эквивалентной нормальной системой.
эквивалентной нормальной системой. 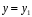 ,
, 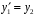 ,
, 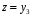 :
: 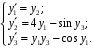
Пример. Представить дифференциальное уравнение третьего порядка
эквивалентной нормальной системой.
Эквивалентная система д.у. первого порядка:
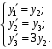
Пример. Найти общее решение системы д.у.
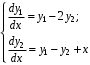 методом исключения неизвестных, преобразовав систему в дифференциальное уравнение второго порядка.
методом исключения неизвестных, преобразовав систему в дифференциальное уравнение второго порядка.Производная первого уравнения системы:
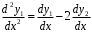 .
.Замена
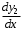 в уравнении
в уравнении 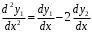 :
: 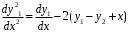 .
. Замена
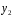 на
на 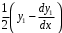 :
: 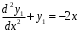 .
. Общее решение д.у.
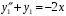 :
: 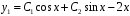 .
. 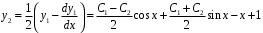 .
.Общее решение системы д.у.:
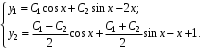
Системы линейных уравнений с постоянными коэффициентами
Пример. Записать систему уравнений
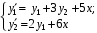 в матричной форме.
в матричной форме. 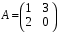 ,
, 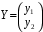 ,
, 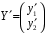 ,
, 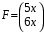 .
.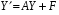 или
или 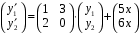 .
.Пример. Установить линейную зависимость или независимость вектор-функций
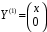 и
и 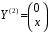 .
. 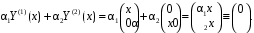
Линейная комбинация тождественно равна нулю только в случае
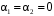 . Вектор-функции линейно независимы.
. Вектор-функции линейно независимы. Пример. Доказать, что если вектор-функции
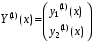 и
и 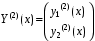 линейно зависимы, то определитель Вронского
линейно зависимы, то определитель Вронского 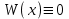
.
Пусть
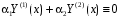 и один из коэффициентов отличен от нуля, например,
и один из коэффициентов отличен от нуля, например, 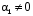 .
. Тогда
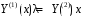 и
и 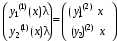 , где
, где 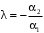 .
. 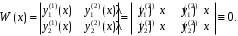
Пример. Установить линейную зависимость или независимость вектор-функций
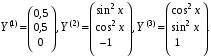
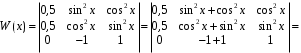
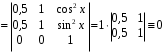
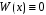 при любых значениях х. Функции линейно зависимы.
при любых значениях х. Функции линейно зависимы.Действительно, существуют отличные от нуля коэффициенты
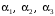 , при которых линейная комбинация
, при которых линейная комбинация 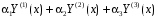 тождественно равна нулю, например,
тождественно равна нулю, например, 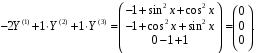
Решение однородных систем линейных уравнений
Пример. Найти общее решение системы
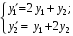 двумя способами.
двумя способами.I способ. Матрица системы:
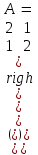 .
. Характеристическое уравнение:
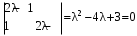 .
.Корни характеристического уравнения:
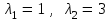 .
.Фундаментальная система решений:
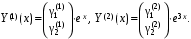
Уравнение для нахождения собственных векторов:
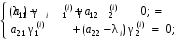
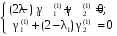 при
при 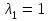 :
: 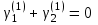 .
.Собственный вектор для
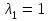 :
: 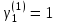 ,
, 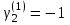
.
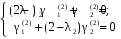 при
при 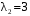 :
: 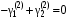 .
.Собственный вектор для
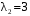 :
: 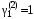 ,
, 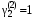 .
.Общее решение системы:
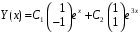
или в скалярной форме
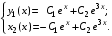
II способ. Корни характеристического уравнения:
 .
.Вид общего решения (таблица 13.2):
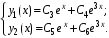
Подстановка решения в первое уравнение системы:
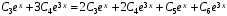 .
.Коэффициенты при
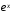 :
: 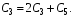
Коэффициенты при
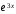 :
: 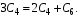
Общее решение системы при
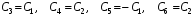 :
: 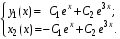
Пример. Двумя способами найти частное решение системы уравнений
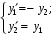 при начальных условиях
при начальных условиях 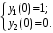 .
.I способ. Матрица системы:
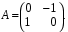
Характеристическое уравнение
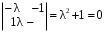 .
.Корни характеристического уравнения:
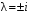 .
.Фундаментальная система решений:
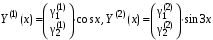 .
.Уравнение для нахождения собственных векторов:
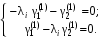
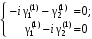 при
при 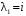 :
: 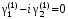 .
.Собственный вектор для
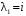 :
: 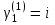
,
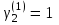 .
.Комплексное решение системы:
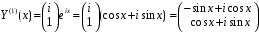 .
.Вещественная и мнимая части комплексного решения:
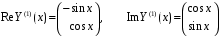 .
.Общее решение системы:
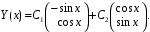
или в скалярной форме
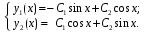
Начальные условия:
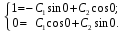
Значения произвольных постоянных:
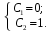
Частное решение, удовлетворяющее начальным условиям:
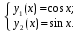
II способ. Корни характеристического уравнения:
Вид общего решения (таблица 13.2):
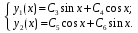
Подстановка решения в первое уравнение системы:
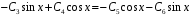 .
.Коэффициенты при sinх:

Коэффициенты при cosх:
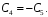
Общее решение системы при
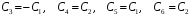 :
: 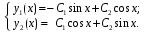
Частное решение, удовлетворяющее начальным условиям:
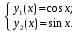
Пример. Найти общее решение системы
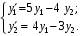
I. Матрица системы
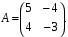
Характеристическое уравнение
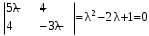 .
.Корни характеристического уравнения:
Фундаментальная система частных решений:
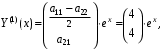
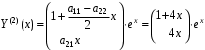 .
. Общее решение системы:
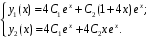
Пример. Найти общее решение системы