Добавлен: 18.10.2024
Просмотров: 36
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Определение реакций связей для двухопорной балки
Определение реакций связей для консольной балки
Определение траектории, скорости и ускорения точки по заданным уравнениям ее движения
Кинематический анализ механической системы при плоском движении
Применение теоремы об изменении кинетической энергии к изучению движения механической системы
Задача 4.
Кинематический анализ механической системы при плоском движении
4.1. Условие задачи
Механическая система (рисунок 2.1) под действием заданных сил и моментов, действующих на ее элементы, из состояния покоя приводится в движение так, что колесо В катится по плоскости. Массы элементов системы mA, mB, углы α и β, момент M, действующие силы F, радиусы колеса B и его радиус инерции ρB, приведены в таблице 2.1. Масса шкива С равна 5 кг, его радиус равен RC = 0,2 м. Коэффициент трения скольжения тела А по поверхности равен f=0,1; коэффициент трения качения колеса В равен fK=0,05RB.
Считая, что шкив С представляет собой сплошной однородный диск, а гибкие связи невесомые и нерастяжимые, определим для заданной механической системы скорости, перемещения и ускорения всех тел, при найденной скорости
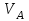 , заданном перемещении
, заданном перемещении 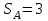 метра и найденном ускорении
метра и найденном ускорении 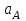 тела
тела  , перемещающегося по вертикальной поверхности (рис. 4.1).
, перемещающегося по вертикальной поверхности (рис. 4.1). 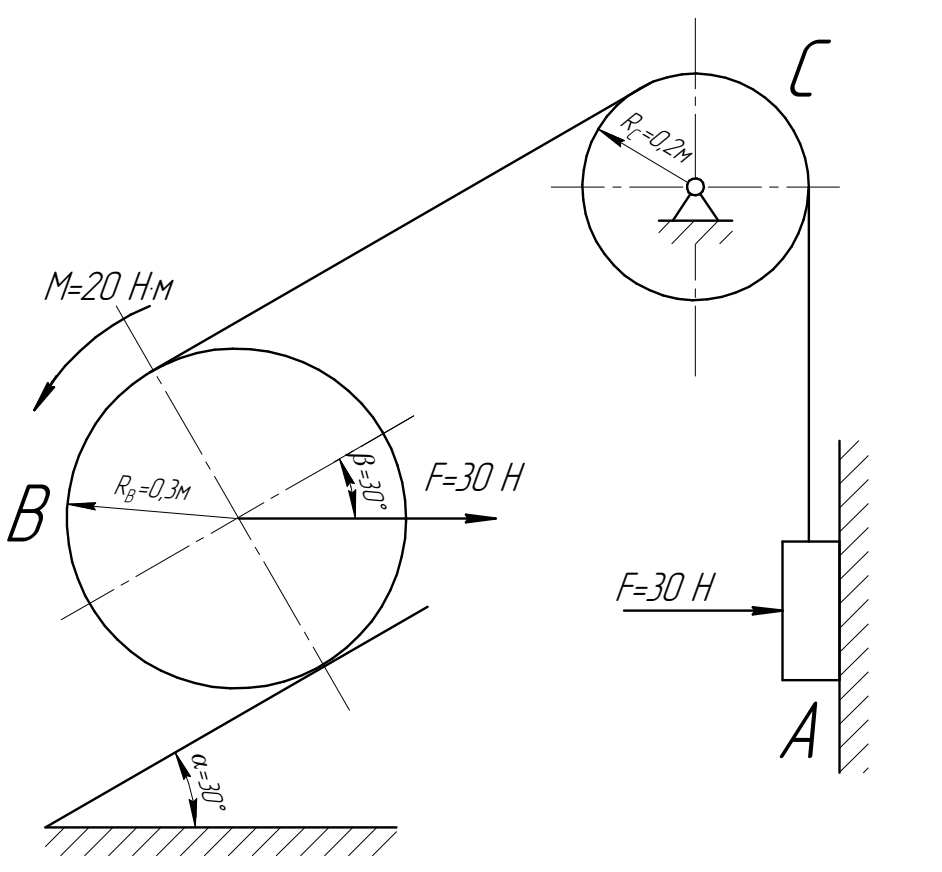 |
| Рис. 4.1. Механическая система при плоском движении (вариант 12) |
Исходные данные:
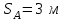 | 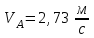 | 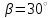 | 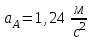 | 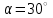 |
Согласно рис. 4.1 имеем
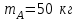 | 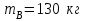 | 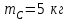 | 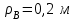 |  |
 |  | 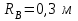 | 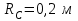 | 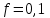 |
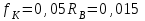 | 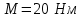 | 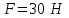 | | |
Здесь
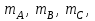 ‒ массы тел механической системы.
‒ массы тел механической системы.4.2. Определение скоростей тел механической системы
Будем считать, что при заданных исходных данных тело
 будет двигаться вниз по вертикальной плоскости. Поэтому вектор скорости
будет двигаться вниз по вертикальной плоскости. Поэтому вектор скорости 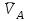 тела
тела  направим вниз вдоль вертикальной плоскости (рис. 4.2). Значение скорости
направим вниз вдоль вертикальной плоскости (рис. 4.2). Значение скорости  для точки
для точки  нам задано по условию (см. решение задачи 5):
нам задано по условию (см. решение задачи 5): 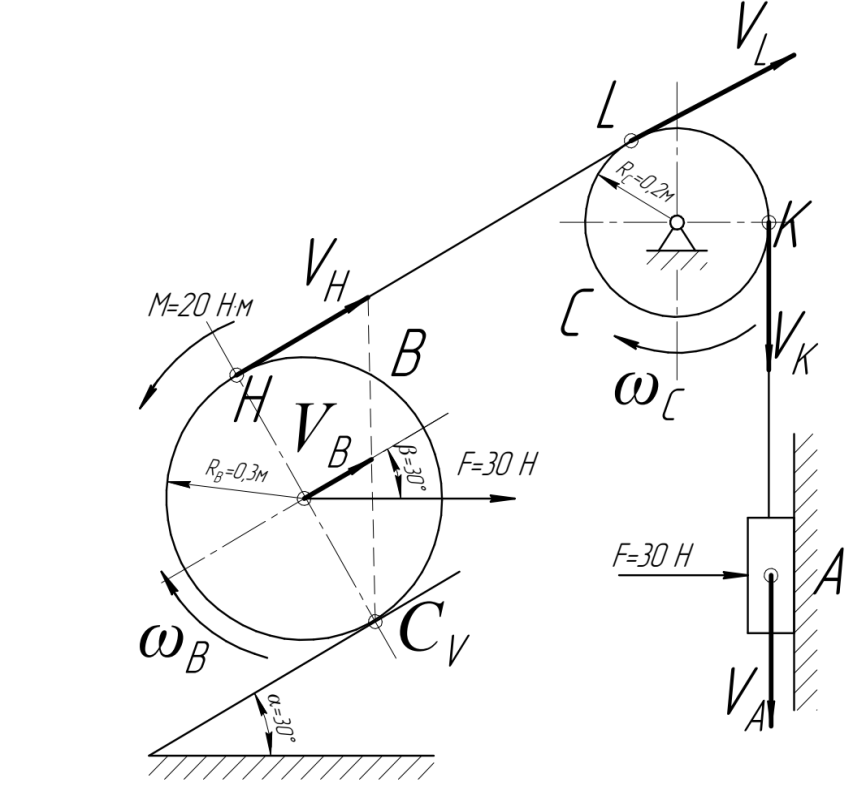 |
| Рис. 4.2. Скорости тел механической системы |
 . . | (4.0) |
К телу
 прикреплена нить (трос), которая наматывается на барабан
прикреплена нить (трос), которая наматывается на барабан  .
.На ободе диска
 в точке
в точке 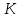 , где трос начинает взаимодействовать с барабаном скорости точек нити и барабана при отсутствии проскальзывания одинаковы.
, где трос начинает взаимодействовать с барабаном скорости точек нити и барабана при отсутствии проскальзывания одинаковы.Учитывая, что нить нерастяжимая, делаем заключение, что скорость

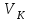 для точки барабана
для точки барабана 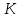 равна скорости
равна скорости  тела А (рис. 4.2):
тела А (рис. 4.2): 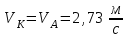 . . | (4.2) |
В то же время точка
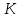 вращается относительно центральной точки
вращается относительно центральной точки  барабана с угловой скоростью
барабана с угловой скоростью 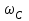 по окружности радиуса
по окружности радиуса 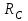 (рис. 4.2).
(рис. 4.2).Поэтому для скорости точки
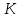 можно записать
можно записать 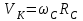 . . | (4.3) |
Подставим Error: Reference source not found в Error: Reference source not found и запишем:
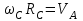 . . | (4.4) |
Из Error: Reference source not found определим угловую скорость
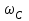 барабана
барабана  :
: 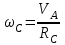 . . | (4.5) |
Рассмотрим теперь точку
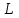 на ободе диска, которая вращается относительно неподвижной точки
на ободе диска, которая вращается относительно неподвижной точки  (место крепления шарнира) с угловой скоростью
(место крепления шарнира) с угловой скоростью  . В этом случае скорость точки
. В этом случае скорость точки 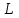 можно определить выражением:
можно определить выражением: 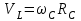 . . | (4.6) |
Подставим Error: Reference source not found в Error: Reference source not found и запишем:
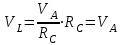 . . | (4.7) |
В точке
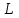 нить касается колеса и поэтому без проскальзывания у нити и колеса в этой точке скорости одинаковы.
нить касается колеса и поэтому без проскальзывания у нити и колеса в этой точке скорости одинаковы.Затем двигаемся по нити до точки
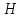 . Так как нить не растяжима, то скорость точки
. Так как нить не растяжима, то скорость точки 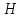 равна скорости точки
равна скорости точки 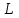 .
. 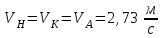 . . | (4.8) |
Далее рассмотрим движение цилиндра
 (рис. 4.2).
(рис. 4.2).В точке
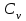 цилиндр соприкасается с наклонной плоскостью и катится по ней без проскальзывания. Поэтому в этой точке
цилиндр соприкасается с наклонной плоскостью и катится по ней без проскальзывания. Поэтому в этой точке 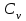 скорости точек цилиндра и наклонной плоскости одинаковы. Но скорость данной точки наклонной поверхности равна нулю. Из этого следует, что и скорость точки цилиндра в этом месте также равна нулю. Таким образом, для цилиндра точка
скорости точек цилиндра и наклонной плоскости одинаковы. Но скорость данной точки наклонной поверхности равна нулю. Из этого следует, что и скорость точки цилиндра в этом месте также равна нулю. Таким образом, для цилиндра точка 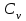 является мгновенным центром скоростей, скорость которого равна нулю:
является мгновенным центром скоростей, скорость которого равна нулю: 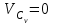 . . | (4.9) |
Считаем, что цилиндр вращается относительно мгновенного центра скоростей с угловой скоростью
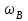 (рис. 4.2).
(рис. 4.2).Для определения угловой скорости
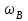 рассмотрим скорость
рассмотрим скорость 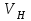 точки
точки  (на ободе цилиндра радиуса
(на ободе цилиндра радиуса 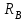 ) при ее вращении относительно мгновенного центра скоростей
) при ее вращении относительно мгновенного центра скоростей  с угловой скоростью цилиндра
с угловой скоростью цилиндра 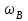 . Она рассчитывается по формуле:
. Она рассчитывается по формуле: 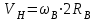 . . | (4.10) |
где
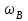 ‒ угловая скорость вращения цилиндра
‒ угловая скорость вращения цилиндра  ,
,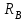 ‒ радиус цилиндра
‒ радиус цилиндра  .
.Из Error: Reference source not found получим
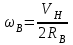 . . | (4.11) |
Подставим Error: Reference source not found в Error: Reference source not found и запишем:
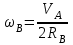 . . | (4.12) |
Рассмотрим теперь точку
 в центре окружности радиуса
в центре окружности радиуса 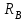 , которая вращается относительно мгновенного центра скоростей
, которая вращается относительно мгновенного центра скоростей  с угловой скоростью цилиндра
с угловой скоростью цилиндра 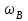 . В этом случае скорость точки
. В этом случае скорость точки  можно определить выражением:
можно определить выражением: 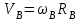 . . | (4.13) |
