Файл: Основы статистического метода исследования общественного здоровья и здравоохранения.docx

Средняя арифметическая величина обладает следующими свойствами:

1) занимает серединное положение в ряду;

2) отражает общую меру количественного признака в совокупности, нивелируя его минимальное и максимальное значение и разнообразие;

3) сумма отклонений всех вариант от средней равна нулю.
Если распределение вариационного ряда отлично от симметричного, то для характеристики среднего уровня признака применять среднюю арифметическую нельзя, т.к. она не будет являться наиболее типичной величиной, характеризующей вариационный ряд. В этом случае обычно применяют медиану, реже моду (так называемые структурные средние).
Медиана – определяется как варианта вариационного ряда, делящая его на две равные части.
В четном ряду медиана может быть рассчитана как средняя арифметическая двух центральных вариант.
Мода – определяется как варианта, значение которой наиболее часто встречается в вариационном ряду.

Как характеристика среднего значения признака мода может быть использована при малом числе наблюдений, когда велико влияние состава совокупности либо крайних вариант на среднюю арифметическую в ассиметричных распределениях.

Средняя арифметическая может быть рассчитана тремя способами. Если число наблюдений при исследовании количественного признака в вариационном ряду небольшое (менее 30), а значение каждой варианты встречается только один раз, расчеты можно вести простым способом:
 
где: M – средняя арифметическая величина;

∑V – сумма всех вариант;

n – число наблюдений.
Если некоторые варианты ряда имеют одинаковые значения, при этом число наблюдений небольшое (менее 30), а разнообразие изучаемого признака низкое, то удобно пользоваться способом вычисления средней арифметической взвешенной:
 
где: M – средняя арифметическая величина;

∑Vp – сумма произведений всех вариант на их частоты;

n – число наблюдений.

---

 

При большом количестве наблюдений и высоком разнообразии изучаемого признака данные способы вычисления средней арифметической неудобны из-за громоздкости расчетов. В этом случае прибегают к способу моментов^3*:


где: M – средняя арифметическая;

A – условная средняя;

i – интервал;

а – условное отклонение от условной средней;

p – частота;

n – число наблюдений.

 

Для расчета средней арифметической величины любым из способов необходимо построить вариационный ряд.
Вариационным рядом называется ряд чисел, расположенных в порядке убывания или возрастания, количественно характеризующий изучаемый признак.

 

Даже при возможности компьютерной обработки количественных данных, построение вариационного ряда является основой их анализа, т.к. позволяет описать распределение количественного признака в статистической совокупности, определить среднее значение признака, его разнообразие, выбирать правильные методики сравнения данных и определения взаимосвязи между признаками. Данные свойства определяются характеристиками ряда - его элементами. Основными элементами вариационного ряда являются:

1. 
   Варианта (V) - каждое число вариационного ряда, показывающее отдельное количественное выражение признака.
   
2. 
   Частота (р) - абсолютная численность отдельной варианты в ряду; сумма всех частот составляет число наблюдений (n).
   
3. 
   Интервал (i) – расстояние между отдельными вариантами или группами в вариационном ряду.
   
4. 
   Средняя арифметическая (M), медиана (Ме), мода (Мо) – характеристики среднего уровня признака.
   
5. 
   Варианты минимальная и максимальная (лимит) – характеризуют разнообразие количественного признака по его крайним значениям.
   
6. 
   Амплитуда (размах) – разница между минимальной и максимальной вариантами; характеризует разнообразие количественного признака по его крайним значениям.
   
7. 
   Среднеквадратическое (стандартное) отклонение (δ) – характеристика разнообразия признака в симметричном (близком к нормальному распределению) вариационном ряду, показывающая его внутреннюю структуру.
   

---

При небольшом количестве наблюдений достаточно построить простой вариационный ряд из имеющихся вариант, расположив их в порядке возрастания. В случае большого количества наблюдений строят сгруппированный вариационный ряд.

Методика построения сгруппированного вариационного ряда сводиться к следующим этапам:

• 
  Первым этапом построения сгруппированного вариационного ряда является определение количества групп в ряду. Чем больше групп, тем более громоздки расчеты; чем меньше групп, тем более скрадывается разнообразие изучаемого признака и снижается точность. Поэтому нежелательно, чтобы количество групп было менее 6 и более 17. Удобно ориентировочно определять количество групп в зависимости от числа наблюдений при помощи специальной таблицы (таб. 7), однако исследователь должен сам решить и обосновать свое решение.
  

 Таблица 7

Число групп в зависимости от числа наблюдений

n (число наблюдений)	31 – 45	46 – 100	101 – 200	200 – 500
r (количество групп)	6 – 7	8 – 10	11 – 12	12 – 17

• 
  Вторым этапом построения сгруппированного вариационного ряда является определение интервала между группами по следующей формуле, округляя полученную величину до целого числа:
  

где: i – величина интервала;

V_макс. – максимальная варианта;

V_мин. – минимальная варианта

r – количество групп.

 

• 
  На третьем этапе определяем начало и конец в каждой группе, согласно значению интервала.
  

---

• 
  На четвертом этапе распределяем варианты по группам в соответствии с их частотами.
  

• 
  На пятом этапе определяем серединную варианту в каждой группе как среднюю арифметическую между крайними вариантами.
  

• 
  Далее для последующего анализа вариационного ряда строим его графическое изображение.
  

Поясним данные этапы на примере. При исследовании уровня гемоглобина у 54 беременных женщин были получены следующие данные: 113, 114, 115, 116, 116, 117, 117, 118, 118, 119, 120, 120, 119, 119, 120, 120, 121, 121, 122, 122, 122, 121, 121, 122, 122, 123, 123, 123, 123, 124, 124, 124, 124, 124, 125, 125, 125, 125, 126, 126, 125, 126, 127, 128, 128, 128, 129, 129, 129, 130, 130, 131, 132, 133 г/л.

1. 
   Поскольку число наблюдений в ряду n = 54, то пусть количество групп будет равно 8 (согласно таблице 7).
   
2. 
   Определим интервал: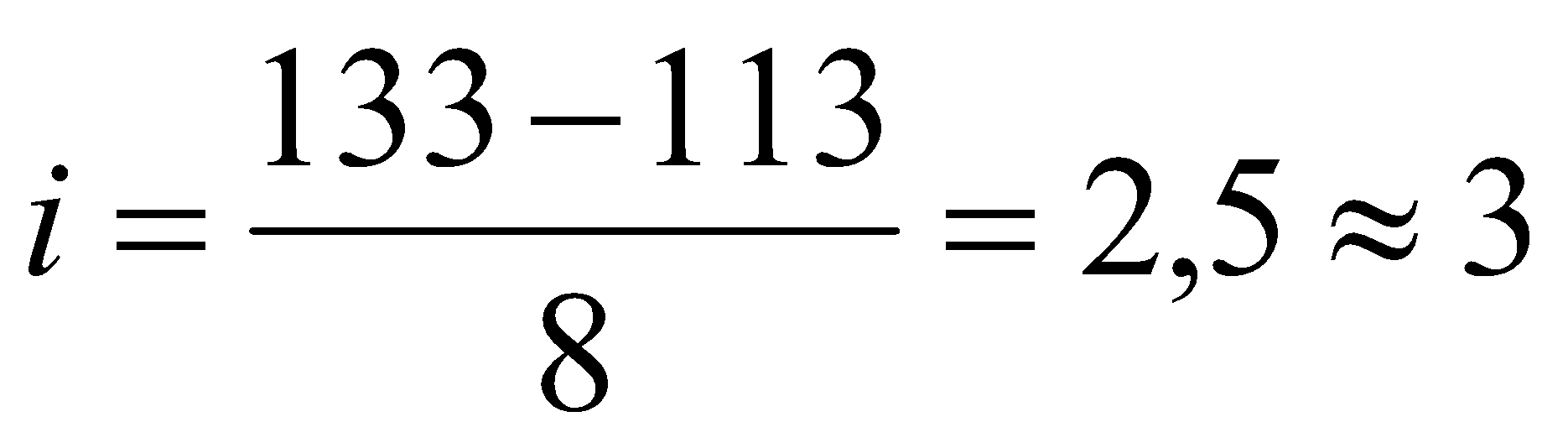  
   
3. 
   Определим начало и конец в каждой группе согласно значению интервала. Так первая варианта равна 113, значит под ней должна располагаться варианта 113 + 3 (значение интервала) = 116, тогда первая группа будет включать в себя варианты от 113 до 115, вторая от 116 до 118 и т.д. Продолжаем осуществлять группировку, пока все варианты вариационного ряда не войдут в состав соответствующих групп (таблица 8). То, что количество групп в результате получилось не 8 а 7 не является ошибкой и является следствием округления величины интервала до целого числа.
   

Таблица 8

Результат третьего этапа построения сгруппированного вариационного ряда

V
113	-	115
116	-	118
119	-	121
122	-	124
125	-	127
128	-	130
131	-	133

4. 
   Распределим варианты по группам в соответствии с их частотами, т.е. в группу 113 – 115 входит 3 варианты, в группу 116 – 118 - 6 вариант и т.д. Результат этапа представлены в таблице 9.
   

Таблица 9

Результат четвертого этапа построения сгруппированного вариационного ряда

V	p
113 - 115	3
116 - 118	6
119 - 121	11
122 - 124	14
125 - 127	9
128 - 130	8
131 - 133	3

5. 
   Определим серединную варианту в каждой группе как среднюю арифметическую между крайними вариантами. Так середина группы 113 – 115 будет равна (113+115):2=114, следующей группы 117 и т.д. В результате получаем сгруппированный вариационный ряд (таблица 10).
   
6. 
   Построим графическое изображение ряда (рис. 12), наглядно иллюстрирующее распределение уровней гемоглобина у беременных женщин, из которого видно, что оно близко к симметричному^4* из чего следуют выводы, что для характеристики среднего уровня гемоглобина можно применять среднюю арифметическую, для характеристики разнообразия – среднеквадратическое отклонение, а при необходимости последующего сравнения данных и определения взаимосвязи между признаками – так называемые параметрические методы^5**.
   

Таблица 10

Сгруппированный вариационный ряд

Vсредняя	p
114	3
117	6
120	11
123	14
126	9
129	8
132	3

---

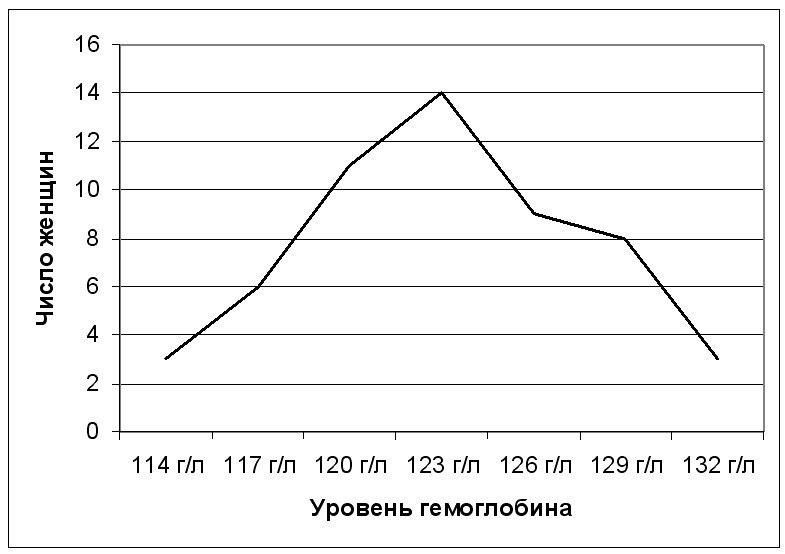
Рисунок 12. Распределение беременных женщин по уровню гемоглобина.

 

По сгруппированному вариационному ряду можно рассчитать среднюю арифметическую способом моментов по формуле:

За условную среднюю (А) можно взять любую варианту вариационного ряда, однако для удобства принято брать варианту, значение которой будет близко к средней арифметической. Обычно за условную среднюю берут моду либо медиану. В данном ряду модой является варианта имеющая значение 123 г/л (см. таблицу 11, условная средняя выделена жирным шрифтом).

Далее необходимо найти условное отклонение вариант от условной средней (а). Если бы определялось истинное отклонение вариант от условной средней (d) то расчет бы проводился по формуле d = V – A (в таблице 11 результаты вычисления d выделены серым фоном). Из таблицы 11 видно, что значения d различаются друг от друга на величину интервала. Для упрощения последующих вычислений рассчитывается не истинное отклонение, а условное (a) – интервал условно принимаем за 1, т.е. каждое отклонение будет отличаться от последующего на 1. Не трудно заметить, что условное отклонение a = d/i (впоследствии при расчете средней арифметической эта допускаемая условность устраняется умножением момента первой степени на значение интервала^6*) Конечно при расчетах нет никакой потребности определять и a, и d, проще сразу установить условное отклонение. В настоящем примере расчеты d приведены исключительно ради объяснения. Далее построчно находим произведение ap, ∑ap и подставляем данные в формулу, получая значение средней арифметической.

Таблица 11

Вычисление данных, необходимых для расчета средней арифметической величины по способу моментов

V	Vсредняя	p	d	а	ap
113 - 115	114	3	-9	-3	-9
116 - 118	117	6	-6	-2	-12
119 - 121	120	11	-3	-1	-11
122 - 124	123	14	0	0	0
125 - 127	126	9	3	1	9
128 - 130	129	8	6	2	16
131 - 133	132	3	9	3	9
	n = 54				∑ap = 2

---