Файл: Бизнесом.docx

Третья подзона находится в убыточной зоне. Она предупре­ждает фирму о грядущей беде, необходимости принятия сроч­ных мер по совершенствованию производства и рационализации продукции, об изменениях стратегии и тактики в области при­нятия управленческих решений. Попадание на этот участок  сигнал бедствия, преддверие беды.

И наконец, четвертая подзона означает одно: это прямой путь к разорению, к полному банкротству. Сюда лучше не попадать!

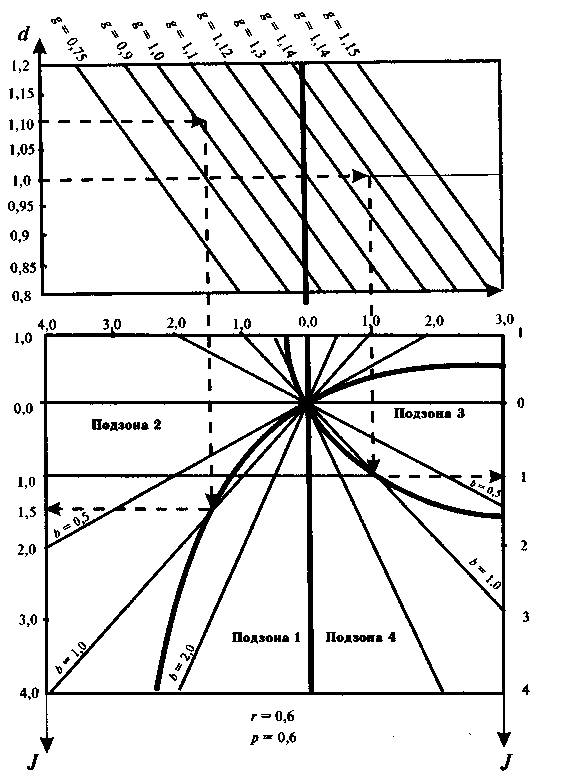
Рис. 4.1. Закономерность изменения индекса прибыли фирмы под действием прибылеобразующих факторов
Построив зоны и все необходимые между ними границы, с использованием параметрической модели рассчитывают индек­сы прибыли с определенным шагом изменения объемов произ­водства продукции (как было сделано в табл. 4.4). Полученные точки соединяют и получают кривую, которая характеризует ис­комую закономерность.

В принципе возможны два вида кривых (обе они представле­ны на рис. 4.1). Первый тип — кривая, идущая слева вверх на­право (в большей своей части она расположена в рентабельной зоне), второй тип — кривая, идущая слева вниз направо (большая ее часть находится в убыточной зоне).

Нетрудно понять, что графика, при умелом ее использова­нии, может стать незаменимым инструментом для выработки стратегии развития производства и тактики ее реализации.
4.4. Границы безубыточности производства

Одним из важнейших условий успешного ведения своего хо­зяйства является безубыточность производства. При этом следу­ет различать абсолютную и относительную безубыточность.

Абсолютная безубыточность представляет собой такое производство, при котором прибыль больше нуля. Границей пере­хода из безубыточного в убыточное производство является при­быль, равная нулю. Следовательно, если принять индекс прибы­ли I = 0, то, используя параметрическую модель, можно устано­вить границу абсолютной безубыточности производства.

Произведем эту операцию с применением модели типа 4.6.



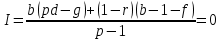
Из этого выражения можно определить границу абсолютной безубыточности производства по любому параметру, т.е. по цене продукции, по её себестоимости, по объёму производства.

---

Простейшие алгебраические преобразования записанной выше формулы дают следующие результаты количественных границ абсолютной безубыточности производства:
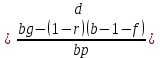( 4.7)

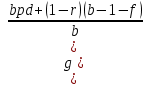(4.8)


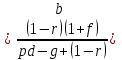(4.9)

Экономический смысл значений этих параметров показыва­ет, что работа предприятия будет прибыльной, если будут вы­держиваться зафиксированные количественные условия, пред­ставленные в выражениях (4.7—4.9).

Пример. Пусть предприятие в базовом периоде имело сле­дующие исходные параметры: p = 1,15 и r = 0,5. Определить, при каком объеме производства продукции будет обеспечена абсо­лютная безубыточность, если планируется увеличить цену реали­зации на 2%, и на столько же снизить себестоимость продукции. Постоянные затраты остаются без изменения.

Для этих исходных данных (d= 1,02; g= 0,98; f= 0,0) опре­делим по формуле 4.9 условие абсолютной безубыточности про­изводства:



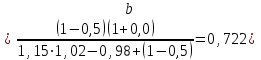
Это значит, что предприятию, чтобы получить хотя бы не­большую прибыль, т.е. прибыль больше нуля, достаточно произ­вести продукции больше чем на 72,2% от базового объема про­изводства.

Относительная безубыточность характеризуется таким со­стоянием производства, при котором полученная предприятием прибыль будет не меньше объемов ее базовой величины. Следо­вательно, чтобы определить границу относительной безубыточ­ности, надо принять индекс прибыли f = 1. Тогда, используя параметрическую модель типа 4.6, можно записать:



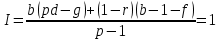
Из полученного выражения определим границу относительной безубыточности производства по любому из Параметров модели.

Алгебраические преобразования позволяют получить сле­дующие выражения для определения относительной безубыточ­ности производства:

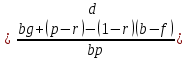(4.10)

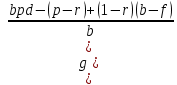(4.11)

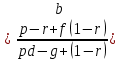(4.12)
Полученные выражения по экономическому смыслу пред­ставляют условия, соблюдение которых позволяет получить прибыль не меньше, чем она была в базовом периоде.

---

Пример. Пусть предприятие в базовом периоде имело рентабельность производства 25% (p = 1,25) и коэффициент переменных затрат r= 0,6.

Для повышения конкурентоспособности своей продукции предприятие повысило ее качество, затратив на это дополнительные ресурсы. Это привело к повышению себестоимости на 15% (т.е. g = 1,15). Одновременно предприятие решило снизить цену на свою продукцию на 10% (т.е. d= 0,9). Определить, при каких условиях предприятие сможет получить прибыль в плановом периоде не ниже, чем в базовом, если условно-постоянные расходы не изменяются (т.е. f= 0,0).

Для решения этой задачи воспользуемся формулой 4.12:



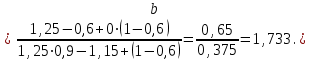
Полученный результат говорит о том, что предприятие при столь жестких исходных условиях может получить прибыль не ниже, чем в базовом периоде, если сможет произвести и реализовать продукции в анализируемом периоде более чем на 73,3 %

Этот пример многому может научить предпринимателя. Его смысл заключается в том, что не следует бояться снижать цены на свои товары и нести дополнительные затраты на повышение их качества. Потери прибыли при этом могут быть компенсированы, и можно даже получить более высокую прибыль. И в этом можно убедиться на рассматриваемом примере, если принять что объем реализации продукции при тех же исходных данных увеличится вдвое (т.е. b = 2,2),

Для определения индекса прибыли можно воспользоваться параметрической моделью типа 4.6:



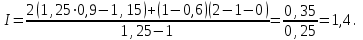
Оказывается, можно существенно снизить цену на свой товар, можно и нужно повысить качество продукции, понеся при этом дополнительные затраты, если при этом значительно повысится продажа товаров. Тогда прибыль существенно может превысить базовый уровень. Недаром на рынке цивилизованных стран пользуется вниманием поговорка: «Не бойтесь занизить цену на свой товар, бойтесь ее завысить!».

Вообще, в рынке, как известно, можно придерживаться различной ценовой политики. Можно, например, при очень высоких ценах на свой товар очень мало его продавать. Но максимально снизить цены и продать большое количество товаров. Это две крайности, две прямо противоположные ценовые политики. Между ними каждая фирма может выбрать какую-то промежуточную политику. Помочь фирмам найти свою нишу на рынке путем установления наиболее предпочтительных цен мо­гут формулы типа 4.7—4.12.

---

4.5. Неопределенность рыночной ситуации и

надежность планово-управленческих решений

В рынке прогноз тех или иных экономических и финансовых показателей даже на незначительную временную перспективу для всех предприятий носит вероятностный характер. Это связано с тем, что на величину этих показателей сильно влияют не только внутренние для предприятия факторы производства, но и много­численные внешние факторы. Учесть их совокупное действие с абсолютной точностью — задача нереальная. Можно лишь при­мерно оценить возможную погрешность ожидаемой величины того или иного показателя в зависимости от рыночной ситуации. А эта ситуация, естественно, носит характер неопределенности.

В таких жестких условиях функционирования предприятию очень важно так спланировать свою деятельность, чтобы хотя бы обеспечить абсолютную или относительную безубыточность про­изводства, т.е. определить те условия, при соблюдении которых предприятие не окажется банкротом и получит прибыль не меньше, чем в базовом периоде.

Одним из возможных оценочных показателей, который может быть применен в процессе выработки планово-управленческого решения на ближайшую перспективу (в пределах года) и который опосредованно будет отражать надежность такого плана, является показатель, названный нами страховым коэффициентом. Для каж­дого решения таких коэффициентов может быть несколько. С од­ной стороны, это коэффициенты по абсолютной и относительной безубыточности, а с другой — коэффициенты по цене товара, по затратам на его производство и по объему реализации продукции.

Рассмотрим экономический смысл страховых коэффициен­тов и определим их величину на примере объема реализации продукции.

Предположим, что предприятие планирует на ближайший квартал продавать свою продукцию по цене d, обеспечив затра­ты на ее производство в размере g. Объем производства и реали­зации продукции планируется установить на уровне b. По от-

четным данным за прошлый квартал предприятие имело коэф­фициент рентабельности производства pи коэффициент пере­менных затрат r.

В результате такого планово-управленческого решения инди­кативный прогноз прибыли предприятия составляет I. А это зна­чит, что если все запланированные параметры будут выдержаны в процессе практической реализации плана, то предприятие полу­чит ту самую прибыль, которую оно себе запрограммировало.

---

Однако реальная экономическая жизнь и хозяйственная ры­ночная ситуация могут существенно изменить запланированные параметры, в частности изменить объем производства и реали­зации продукции. Предположим, что объем производства соста­вит уровень, при котором наступает граница абсолютной без­убыточности производства. Определим этот уровень как b₀

Формула 4.9 дает возможность установить, от чего и в каком размере объема реализации наступает искомая граница.

Тогда величина страхового коэффициента составит:



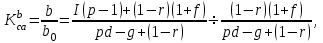
где b— объем реализации продукции плану (может быть од­нозначно определен из формулы 4.6 и заменен равным ему вы­ражением);

b₀ — объем реализации продукции, при котором наступает граница абсолютной безубыточности производства, определяемый по формуле 4.9.

Произведя соответствующие преобразования полученного выражения, получим значение страхового коэффициента абсо­лютной безубыточности по объему реализации продукции:

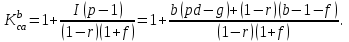(4.13)

По аналогии определим величину коэффициента относи­тельной безубыточности с использованием формул 4.6 и 4.12:



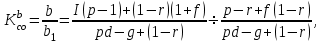
где b₁ — объем реализации продукции, при котором наступа­ет граница относительной безубыточности производства.

После преобразований получим:

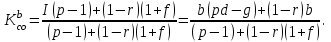(4.14)



Зададим конкретные числа и произведем расчет страховых коэффициентов по объему реализации продукции.

Пусть предприятие в базовом периоде имело p = 1,15 и r= 0,5.

Для анализируемого периода предприятие планирует обеспе­чить объем реализации продукции b = 1,2, затраты на уровне g= 0,98 и цену реализации d = 1,05. Условно-постоянные затра­ты не меняются (т.е. f = 0). Определим страховые коэффициен­ты для принятого планово-управленческого решения.

По формуле 4.13 рассчитаем страховой коэффициент абсо­лютной безубыточности производства:

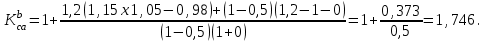
По формуле 4.14 исчислим страховой коэффициент относи­тельной безубыточности производства:



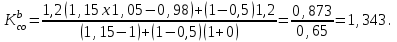
Полученный результат свидетельствует о тех запасах прочно­сти, которыми обладает плановая величина объема реализации продукции. Так, можно констатировать, что предприятие будет работать с прибылью, если объем реализации продукции в силу ряда внешних и внутренних причин не снизится против заплани­рованной величины больше чем на 74,6% и превысит

---